Форд-Фалкерсон (Ford-Falkerson)

Решает задачу нахождения максимального потока транспортной сети.
Алгоритм:

1. Обнуляем все потоки. Остаточная сеть изначально совпадает с исходной сетью.
2. В остаточной сети находим любой путь из источника в сток. Если такого пути нет, останавливаемся.
3. Пускаем через найденный путь (он называется увеличивающим путём или увеличивающей цепью) максимально возможный поток:

a. На найденном пути в остаточной сети ищем ребро с минимальной пропускной способностью .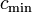

b. Для каждого ребра на найденном пути увеличиваем поток на 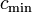, а в противоположном ему — уменьшаем на .

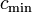c. Модифицируем остаточную сеть. Для всех рёбер на найденном пути, а также для противоположных им рёбер, вычисляем новую пропускную способность. Если она стала ненулевой, добавляем ребро к остаточной сети, а если обнулилась, стираем его.

Возвращаемся на шаг 2

Алгоритм (формально):
Вход: Граф с пропускной способностью , источник и сток
Выход:Максимальный поток 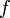из в 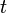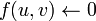для всех ребер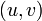

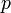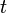2. Пока есть путь из в в 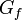, такой что 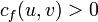для всех ребер :

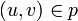a. Найти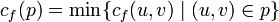

b. Для каждого ребра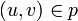

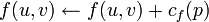
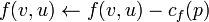
Сложность:O(E*f), т.к. поток увеличивется максимум на 1

Алгоритм Эдмонса-Карпа- то же самое но поиск пути – BFS (кратчайший) – O(VE^2)

Декартово дерево

Декартово дерево — это двоичное дерево, в узлах которого хранятся:

· ссылки на правое и левое поддерево;

· ссылка на родительский узел (необязательно);

· ключ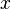и и 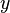, которые являются двоичным деревом поиска по ключу 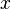и двоичной кучей по ключу 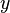; а именно, для любого узла дерева :

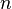o ключи 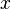узлов правого (левого) поддерева больше (меньше либо равны) ключ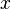а узла ;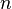

o ключи 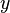узлов правого и левого детей больше либо равны ключу 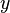узла .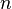

Ссылка на родительский узел не обязательна, она желательна только для линейного алгоритма построения дерева.
По сути, декартово дерево - это структура данных, объединяющая в себе бинарное кучу и двоичное дерево поиска.
Декартово дерево не является самобалансирующемся деревом в обычном смысле (в отличие от красно-черных деревьев).
Преимущества:
1) Легко и быстро реализуется, в отличие от красно-черных деревьев.
2) Для случайного набора ключей y (относительно кучи) хорошо строится.
3) Операция “разделить по ключу х” выполняется за линейное время.
Недостатки:
1) Большие расходы памяти: в каждой вершине нужно хранить два-три указателя и два ключа.
2) Скорость доступа в худшем случае - O(n), поэтому декартово дерево не применяется в ядрах ОС.

Операции в декартовом дереве:

Операция Merge принимает на вход два декартовых дерева L и R. От нее требуется слить их в одно, тоже корректное, декартово дерево T. Следует заметить, что работать операция Merge может не с любыми парами деревьев, а только с теми, у которых все ключи одного дерева ( L ) не превышают ключей второго ( R ).

Алгоритм работы Merge очень прост. Какой элемент станет корнем будущего дерева? Очевидно, с наибольшим приоритетом. Кандидатов на максимальный приоритет у нас два — только корни двух исходных деревьев. Сравним их приоритеты; пускай для однозначности приоритет y левого корня больше, а ключ в нем равен x. Новый корень определен, теперь стоит подумать, какие же элементы окажутся в его правом поддереве, а какие — в левом.

Легко понять, что все дерево R окажется в правом поддереве нового корня, ведь ключи-то у него больше x по условию. Точно так же левое поддерево старого корня L.Left имеет все ключи, меньшие x, и должно остаться левым поддеревом, а правое поддерево L.Right… а вот правое должно по тем же соображениям оказаться справа, однако неясно, куда тогда ставить его элементы, а куда элементы дерева R?

Стоп, почему неясно? У нас есть два дерева, ключи в одном меньше ключей в другом, и нам нужно их как-то объединить и полученный результат привесить к новому корню как правое поддерево. Просто рекурсивно вызываем Merge для L.Right и дерева R, и возвращенное ею дерево используем как новое правое поддерево. Результат налицо.

На рисунке синим цветом показано правое поддерево результирующего дерева после операции Merge и связь от нового корня к этому поддереву.

Симметричный случай — когда приоритет в корне дерева R выше — разбирается аналогично. И, конечно, надо не забыть про основу рекурсии, которая в нашем случае наступает, если какое-то из деревьев L и R, или сразу оба, являются пустыми.

Исходныйкод Merge:

Merge(Treap &t, Treap t1, Treap t2)
if t1 == NULL or t2 == NULL
if t1 != NULL
t = t1;
else
t = t2;
else if t1.y > t2.y
Merge(t1.right, t1.right, t2);
t = t1;
else
Merge(t2.left, t1, t2.left);
t = t2;

ТеперьобоперацииSplit. На вход ей поступает корректное декартово дерево T и некий ключ x₀. Задача операции — разделить дерево на два так, чтобы в одном из них ( L ) оказались все элементы исходного дерева с ключами, меньшими x₀, а в другом ( R ) — с большими. Никаких особых ограничений на дерево не накладывается.

Рассуждаем похожим образом. Где окажется корень дерева T? Если его ключ меньше x₀, то в L, иначе в R. Опять-таки, предположим для однозначности, что ключ корня оказался меньше x₀.

Тогда можно сразу сказать, что все элементы левого поддерева T также окажутся в L — их ключи ведь тоже все будут меньше x₀. Более того, корень T будет и корнем L, поскольку его приоритет наибольший во всем дереве. Левое поддерево корня полностью сохранится без изменений, а вот правое уменьшится — из него придется убрать элементы с ключами, большими x₀, и вынести в дерево R. А остаток ключей сохранить как новое правое поддерево L. Снова видим идентичную задачу, снова напрашивается рекурсия!

Возьмем правое поддерево и рекурсивно разрежем его по тому же ключу x₀ на два дерева L' и R'. После чего становится ясно, что L' станет новым правым поддеревом дерева L, а R' и есть непосредственно дерево R — оно состоит из тех и только тех элементов, которые больше x₀.

Симметричный случай, при котором ключ корня больше, чем x₀, тоже совершенно идентичен. Основа рекурсии здесь — случаи, когда какое-то из поддеревьев пустое. Ну и исходный код функции:Split(Treap t, int k, Treap &t1, Treap &t2)
if t == NULL
t1 = t2 = NULL;
else if k > t.x
Split(t.right, k, t.right, t2);
t1 = t;
else
Split(t.left, k, t1, t.left);
t2 = t;

Оценим время работы операции 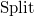. Во время выполнения вызывается одна операция 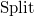для дерева хотя бы на один меньшей высоты и делается ещё 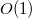операция. Тогда итоговая трудоёмкость этой операции равна 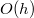, где 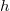— высота дерева.

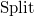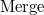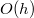Рассуждая аналогично операции приходим к выводу, что трудоёмкость операции равна , где 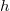— высота дерева.

Insert:
Операция 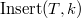добавляет в дерево 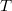элемент 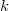, где 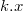— ключ, а 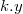— приоритет.
Представим что элемент 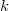, это декартово дерево из одного элемента, и для того чтобы его добавить в наше декартово дерево 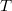, очевидно, нам нужно их слить. Но 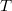может содержать ключи как меньше, так и больше ключа 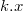, поэтому сначала нужно разрезать 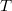по ключу .

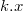1. Разобьём наше дерево по ключу, который мы хотим добавить, то есть.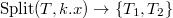

2. Сливаем первое дерево с новым элементом, то есть .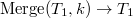

3. Сливаем получившиеся дерево со вторым, то есть .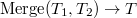

С удалением тоже не возникает никаких вопросов. Пускай нас просят удалить из декартова дерева элемент с ключем x. Сейчас я предполагаю, что вы разобрались с равенством ключей, отдав преимущество левой стороне: в правом поддереве вершины с ключем x другие элементы с тем же ключем не встречаются, а вот в левом могут. Тогда совершим следующую последовательность действий:

1. Разделим сначала дерево по ключу x-1. Все элементы, меньшие либо равные x-1, отправились в левый результат, значит, искомый элемент — в правом.

2. Разделим правый результат по ключу x (здесь стоит быть аккуратным с равенством!). В новый правый результат отправились все элементы с ключами, большими x, а в «средний» (левый от правого) — все меньшие либо равные x. Но поскольку строго меньшие после первого шага все были отсеяны, то среднее дерево и есть искомый элемент.

3. Теперь просто объединим снова левое дерево с правым, без среднего, и дерамида осталась без ключей x.

Поиск k-ой порядковой статистики

Алгоритм ясен: смотрим в корень дерева и на размер его левого поддерева S_L, размер правого даже не понадобится.
Если S_L = K, то искомый элемент мы нашли, и это — корень.
Если S_L > K, то искомый элемент находится где-то в левом поддереве, спускаемся туда и повторяем процесс.
Если S_L < K, то искомый элемент находится где-то в правом поддереве. Уменьшим K на число S_L+1, чтобы корректно реагировать на размеры поддеревьев справа, и повторим процесс для правого поддерева.

Ключевым вопросом все так же остается тот факт, что мы до сих пор не знаем, как поддерживать в дереве корректные значения size. Ведь после первого же добавления в дерево нового ключа все эти числа пойдут прахом, а пересчитывать их каждый раз заново — O(N)! Впрочем, нет. O(N) это заняло бы после какой-нибудь операции, которая полностью перекособочила дерево в структуру непонятной конструкции. А здесь добавление ключа, которое действует аккуратнее и не задевает все дерево, а только его маленькую часть. Значит, можно обойтись меньшей кровью.

Как вы помните, у нас с вами все делается, так сказать, через Split и Merge. Если приспособить эти две основные функции под поддержку дополнительной информации в дереве — в данном случае размеров поддеревьев — то все остальные операции автоматически станут выполняться корректно, ведь своих изменений в дерево они не вносят (за исключением создания элементарных деревьев из одной вершины, в которых Size нужно не забыть установить по дефолту в 1!).
Я начну с модификации операции Merge.

Сделаем индукционное предположение: пускай после выполнения Merge на поддеревьях в них все уже подсчитано верно. Тогда имеем следующее положение вещей: в левом поддереве размеры подсчитаны верно, т.к. его никто не трогал; в правом тоже подсчитаны верно, т.к. это результат работы Merge. Восстановить справедливость осталось лишь в самом корне нового дерева! Ну так просто пересчитаем его перед завершением (size = left.size + right.size + 1), и теперь Merge полностью создала все новое дерево, в каждой вершине которого — правильный размер поддерева.

Знакомое индукционное предположение — пускай рекурсивные вызовы Split все подсчитали верно — поможет нам и в этот раз. Тогда размеры в T.Left корректны — их никто не трогал; размеры в L' корректны — это левый результат Split; размеры в R' корректны — это правый результат Split. Перед завершением нужно восстановить справедливость в корне (x; y) будущего дерева L — и ответ готов.

Неявные декартовы деревья

Вспомним-ка еще раз структуру дерамиды. В ней есть ключ x, по которому дерамида есть дерево поиска, случайный ключ y, по которому дерамида есть куча, а также, возможно, какая-то пользовательская информация с (cost). Давайте совершим невозможное и рассмотрим дерамиду… без ключей x. То есть у нас будет дерево, в котором ключа x нет вообще, а ключи y — случайные. Соответственно, зачем оно нужно — вообще непонятно :)

На самом деле расценивать такую структуру стоит как декартово дерево, в котором ключи x все так же где-то имеются, но нам их не сообщили. Однако клянутся, что для них, как полагается, выполняется условие двоичного дерева поиска. Тогда можно представить, что эти неизвестные иксы суть числа от 0 доN-1 и неявно расставить их по структуре дерева:

Получается, что в дереве будто бы не ключи в вершинах проставлены, а сами вершины пронумерованы. Причем пронумерованы в уже знакомом с прошлой части порядке in-order обхода. Дерево с четко пронумерованными вершинами можно рассматривать как массив, в котором индекс — это тот самый неявный ключ, а содержимое — пользовательская информация c. Игреки нужны только для балансировки, это внутренние детали структуры данных, ненужные пользователю. Иксов на самом деле нет в принципе, их хранить не нужно.

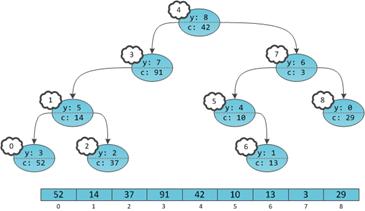
В отличие от прошлой части, этот массив не приобретает автоматически никаких свойств, вроде отсортированности. Ведь на информацию-то у нас нет никаких структурных ограничений, и она может храниться в вершинах как попало.

Теперь стоит поговорить о том, зачем такая трактовка вообще нужна.
Например, вам никогда не хотелось слить два массива? То есть просто приписать один из них в конец другого, при этом не копируя в цикле все элементы второго за O(N). С декартовым деревом по неявному ключу у вас такая возможность есть: ведь операцию Merge у нас никто не отбирал.

Операция Merge, как вы помните, полагается на то, что все ключи левого входного дерева L не превосходят ключей правого входного дерева R. В предположении, что это условие выполняется, она производит слияние, не обращая внимания на ключи в принципе: в процессе выполнения алгоритма сравниваются лишь приоритеты.

Получается, что операцию Merge мы с вами здесь обманываем самым наглым образом: она рассчитывает, что ей дадут деревья с упорядоченными ключами, а мы ей подсовываем деревья вообще без ключей :) Однако предположение что в деревьях есть явные ключи, и они упорядочены, заставит её слить деревья так, что ключи L окажутся по структуре дерева в некотором смысле раньше, чем ключи R — ведь условие дерева поиска должно выполняться. То есть: если в дереве L было N элементов, а в дереве R, соответственно, M элементов, то после слияния элементы дерева R автоматически приобретут неявные номера от N до N+M-1. По структуре дерева операция Merge их распределит автоматически надлежащим образом, а приоритеты, которые она учитывает, выполнят «квази-балансировку». Таким образом, «массив» R мы как бы приписали справа к «массиву» L.

Теперь настала пора Split. Ее так просто обмануть уже не получится: операцию Split, наоборот, не интересуют приоритеты, она сравнивает лишь ключи. Придется задуматься, как она будет сравнивать вершины в неявном дереве. Хотя на самом деле проблема лежит выше: а что вообще выполняет в новой структуре данных операция Split? Раньше она разрезала дерево по ключу, но здесь у нас и ключей-то нет, по которым требуется разрезать.

Ключей нет, однако есть их неявное представление — индексы массива. Таким образом, суть разрезания несколько изменилась: мы хотим расщепить дерево на два так, чтобы в левом оказалось ровно x₀элементов, а в правом — все остальные. В «массивной» трактовке это означает отделение от массива x₀элементов с начала в новый массив.

Как выполнить новую операцию Split? Она рассматривает, как и раньше, два случая: корень T окажется в левом результате L либо в правом R. В левом он окажется, если его индекс в массиве меньше x₀, в противном случае — в правом. А что такое индекс вершины дерева в массиве? Мы ведь с ним уже умеем работать со второй части: достаточно хранить в вершинах дерева размеры поддеревьев. Тогда процесс выбора легко восстанавливается.

Пусть S_L — размер левого поддерева (T.Left.Size).
Если S_L+1 ≤ x₀, то корень будет в левом результате. Значит, нужно рекурсивно разрезать правое поддерево. Но разрезать по другому ключу, по x₀-S_L-1, потому что S_L+1 элемент уже попал в искомый левый результат.
Если S_L+1 > x₀, то корень будет в правом результате. Теперь нужно рекурсивно разрезать левое поддерево. Этот случай не совсем симметричен, как раньше: разрезаем мы поддерево все по тому же ключу x₀, потому как на данном шаге рекурсии отщепляли элементы в правый результат, а не в левый.

Алгоритм построения явной дучи за линейное время
Будем строить дерево слева направо, то есть начиная с 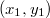по 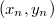, при этом помнить последний добавленный элемент 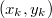. Он будет самым правым, так как у него будет максимальный ключ, а по ключам декартово дерево представляет собой двоичное дерево поиска. При добавлении 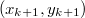, пытаемся сделать его правым сыном 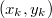, это следует сделать если 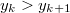, иначе делаем шаг к предку последнего элемента и смотрим его значение 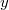. Поднимаемся до тех пор, пока приоритет в рассматриваемом элементе меньше приоритета в добавляемом, после чего делаем 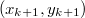его правым сыном, а предыдущего правого сына делаем левым сыном .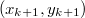