Система непересекающихся множеств. Алгоритм Крускала.

Алгоритм Крускала

Sort(E) – по возрастанию веса

Для каждого ребра e из E MakeSet(e)

For (u,v) из E (уже по возрастанию веса)

If (FindSet(u) != FindSet(v))

Union(u->Set, v->Set)

Оценка

До начала работы алгоритма необходимо отсортировать рёбра по весу, это требует O(E × log(E)) времени. После чего компоненты связности удобно хранить в виде системы непересекающихся множеств. Все операции в таком случае займут O(E × α(E, V)), где α — функция, обратная к функции Аккермана. Поскольку для любых практических задач α(E, V) < 5, то можно принять её за константу, таким образом общее время работы алгоритма Крускала можно принять за O(E * log(E)).

Система непересекающихся множеств

Эта структура данных предоставляет следующие возможности. Изначально имеется несколько элементов, каждый из которых находится в отдельном (своём собственном) множестве. За одну операцию можно объединить два каких-либо множества, а также можно запросить, в каком множестве сейчас находится указанный элемент. Также, в классическом варианте, вводится ещё одна операция — создание нового элемента, который помещается в отдельное множество.

Таким образом, базовый интерфейс данной структуры данных состоит всего из трёх операций:

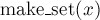· — добавляет новый элемент 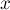, помещая его в новое множество, состоящее из одного него.

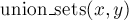· — объединяет два указанных множества (множество, в котором находится элемент 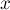, и множество, в котором находится элемент ).

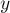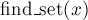· — возвращает, в каком множестве находится указанный элемент 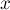. На самом деле при этом возвращается один из элементов множества (называемый представителем или лидером (в англоязычной литературе "leader")). Этот представитель выбирается в каждом множестве самой структурой данных (и может меняться с течением времени, а именно, после вызовов ).

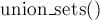Например, если вызов 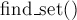для каких-то двух элементов вернул одно и то же значение, то это означает, что эти элементы находятся в одном и том же множестве, а в противном случае — в разных множествах.

Описываемая ниже структура данных позволяет делать каждую из этих операций почти за 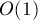в среднем (более подробно об асимптотике см. ниже после описания алгоритма).

Определимся сначала, в каком виде мы будем хранить всю информацию.

Множества элементов мы будем хранить в виде деревьев: одно дерево соответствует одному множеству. Корень дерева — это представитель (лидер) множества.

При реализации это означает, что мы заводим массив 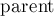, в котором для каждого элемента мы храним ссылку на его предка в дерева. Для корней деревьев будем считать, что их предок — они сами (т.е. ссылка зацикливается в этом месте).

Наивная реализация

Мы уже можем написать первую реализацию системы непересекающихся множеств. Она будет довольно неэффективной, но затем мы улучшим её с помощью двух приёмов, получив в итоге почти константное время работы.

Итак, вся информация о множествах элементов хранится у нас с помощью массива .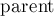

Чтобы создать новый элемент (операция 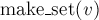), мы просто создаём дерево с корнем в вершине 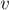, отмечая, что её предок — это она сама.

Чтобы объединить два множества (операция 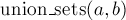), мы сначала найдём лидеров множества, в котором находится 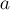, и множества, в котором находится 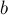. Если лидеры совпали, то ничего не делаем — это значит, что множества и так уже были объединены. В противном случае можно просто указать, что предок вершины 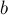равен 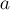(или наоборот) — тем самым присоединив одно дерево к другому.

Наконец, реализация операции поиска лидера ( 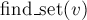) проста: мы поднимаемся по предкам от вершины 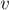, пока не дойдём до корня, т.е. пока ссылка на предка не ведёт в себя. Эту операцию удобнее реализовать рекурсивно (особенно это будет удобно позже, в связи с добавляемыми оптимизациями).

Эвристика сжатия пути

Эта эвристика предназначена для ускорения работы .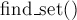

Она заключается в том, что когда после вызова 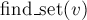мы найдём искомого лидера 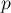множества, то запомним, что у вершины 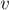и всех пройденных по пути вершин — именно этот лидер 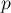. Проще всего это сделать, перенаправив их 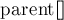на эту вершину .

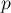Таким образом, у массива предков 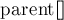смысл несколько меняется: теперь это сжатый массив предков, т.е. для каждой вершины там может храниться не непосредственный предок, а предок предка, предок предка предка, и т.д.

С другой стороны, понятно, что нельзя сделать, чтобы эти указатели 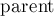всегда указывали на лидера: иначе при выполнении операции 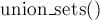пришлось бы обновлять лидеров у 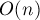элементов.

Таким образом, к массиву 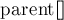следует подходить именно как к массиву предков, возможно, частично сжатому.