История развития математики в России

Предки русского народа — славяне — с незапамятных времён жили на землях Средней и Восточной Европы. Первые письменные упоминания о славянах встречаются в книгах древних римлян, написанных в самом начале нашей эры. Арабские книги говорят о том; что в середине первого тысячелетия славяне вели большую торговлю с греками, арабами и другими народами и храбро воевали с иноземцами, которые пытались их покорить. В X веке нашего летосчисления у славян появилась письменность. С этого времени начинается «писаная» история Древней Руси.

У славян, как и у всех других народов, первым учителем математики была жизнь, практика.

В XVI веке при Иване Грозном на Руси появляются первые рукописные учебники по математике, а немного позже — печатные книги о применении математики для разных практических нужд, например, «Книге сошного письма» и «Устав ратных, пушечных и иных дел, касающихся до воинской науки».

В 1134 году новгородский монах Кирик написал сочинение «...о том, как узнать человеку числа всех лет». Это самый древний дошедший до нас письменный памятник славянской математики.

Первые сведения о развитии математики на Руси относятся к IX-XII вв. (древнерусская нумерация, метрология, первые системы дробей и др.). В Древней Руси времен Ярослава Мудрого (978-1054) уже существовали общеобразовательные школы древнерусского права “Русская правда” и в памятниках духовного содержания: “Книга святых тайн Еноха”, “Шестоднев”, “Толковая палея” и др.

Особенно важную роль в развитии русской науки сыграла книга «Арифметика, или наука числительная», написанная Леонтием Филипповичем Магницким. «Арифметика» Магницкого была издана при Петре I, в 1703 году, и долгое время была настольной книгой всех образованных русских людей. Великий русский учёный Михаил Васильевич Ломоносов знал её наизусть и называл её вместе с учебником грамматики «вратами своей учёности».

Рис. 1. «Арифметика» Магницкого

Книга Магницкого называлась «Арифметика», но, кроме арифметики, там были начала алгебры, геометрии, тригонометрии и даже немного мореходной астрономии. Это была настоящая энциклопедия по математике, в которой каждое правило, каждый приём подробно разъяснялся и подкреплялся решением примеров и практических задач.

Замечательной книгой Магницкого закончилась многовековая история древнерусской математики.

О, Русь – великий звездочет!

Как звезд не свергнуть с высоты,

Так век неслышно протечет,

Не тронув этой красоты.

Как будто древний этот вид

Раз навсегда запечатлен

В душе, которая хранит

Всю красоту былых времен…

Задачи Древней Руси

Изучая историю развития математикис древних времен России, стало понятно, что математика прошла гигантский путь. За это время произошли события от зарождения счета на пальцах до сложнейших теорем.

Старинные математические задачи

Рассмотрим особенности ряда старинных математических задач и возможные способы их решения в современной практике решения задач.

В большинстве русских математических рукописей и печатных книг старого времени встречаются занимательные задачи. Такие задачи есть и в “Арифметике” Л. Ф. Магницкого.

Каждая задача облекается автором в практическую или просто интересную форму. Самая яркая характеристика задач «Арифметики» — прикладной характер задач. Особенно убедитель­но это проявляется в удовлетворении запросов основного потребителя арифметических познаний — купечества. Практически вся третья часть «Арифметики политики» посвящена тройно­му правилу и представляет из себя решение задач торговли.

Напомню, что славяне без малого тысячу лет назад отлично владели четырьмя действиями арифметики, свободно обращались с очень большими целыми числами и с очень маленькими дробями. Думаю, что именно поэтому, все задачи решались путем логических рассуждений.

Старинная задача № 1

“Некий человек нанял работника на год, обещав ему дать 12 рублев и кафтан. Но тот, проработав 7 месяцев, восхотел уйти и просил достойной платы с кафтаном. Он же (хозяин) дал ему по достоинству расчет 5 рублев и кафтан, и знать надлежит, какой цены оный кафтан был”.

Рис. 4 (Иллюстрация к задаче)Рис. 5 (Иллюстрация к задаче)

I способ.

Можно вычислить по действиям, рассуждая логически.

Работник не получил 12 – 5 = 7 (руб.) за 12 – 7 = 5 (месяцев),

поэтому за один месяц ему платили 7:5 = 1,4 (руб.), а за 7 месяцев он получил 7 ·1,4 = 9,8 (руб.), тогда кафтан стоил 9,8 – 5 = 4,8 (руб.).

II способ.

Пусть x руб. — стоимость кафтана.

Алгебраическое решение задачи приводит к уравнению, применяя основное свойство пропорции.

(x + 12):12 = = (x + 5):7

Х = 4,8 . Итак, кафтан стоил 9,8 – 5 = 4,8 (руб).

Старинная задача №2

Говорит дед внукам:

«Вот вам 130 орехов.

Разделите их на 2 части так, чтобы меньшая часть, увеличенная в 4 раза, равнялась бы большей части, уменьшенной в 3 раза».

Как разделить орехи?Рис. 6 (Иллюстрация к задаче)

I способ.

1Уменьшив втрое количество орехов в большей части, мыполучим их столько же, как в четырех меньших частях.

Значит, большая часть должна содержать в 3X4= 12 разбольше орехов, чем меньшая, а общее число орехов должнобыть в 13 раз больше, чем в меньшей части.

Поэтому меньшая часть должна содержать 130:13=10 орехов,а большая 130 — 10 = 120 орехов.

II способ.

Пусть x орехов в меньшей части.

Алгебраическое решение задачи приводит к уравнению

4х:1=(130-х):3

х = 10.

Итак, меньшая часть должна содержать 130:13=10 орехов,а большая 130 — 10 = 120 орехов.

Старинная задача №3

Двое ели сливы. Один сказал другому. «Даймне свои две сливы, тогда будет у нас слив поровну»,— на что другой ответил: «Нет, лучше ты дай мне свои две сливы, — тогда у

меня будет в два раза больше, чем у тебя». Сколько слив было у каждого?

I способ.

Рис. 7 (Иллюстрация к задаче)

Так как передача двух слив уравнивает число слив у собеседников, то у одного из них на четыре сливы больше, чем у другого.

Если же человек, у которого слив меньше, две сливы отдаст человеку, у которого их больше, то разница увеличится до 8 слив.

Поскольку второй человек тогда будет иметь слив в два раза больше, то ясно, что у одного из них после передачи будет 8 слив, а у другого 16 слив.

Следовательно, до передачи двух слив у одного было 10 слив, а у другого было 14 слив.

II способ.

Пусть x слив было у первого собеседника, а у слив у второго.

Алгебраическое решение задачи приводит к системе уравнений. Это решение мне помог найти старший брат.

х + 2 = у – 2,

2(х - 2) = у+2.

х = 10, у = 14.

Исходя из решения системы уравнений, получаем, что до передачи двух слив у одного было 10 слив, а у другого было 14 слив.

2.3. Задача из “Счетной мудрости”

Идет корабль по морю, на нем мужеска полу и женска 120 человек. Найму дали 120 гривен, мущины дали по 4 алтына, а женщины дали по 3 алтына с человека. Сколько мужеска полу было и женска порознь? (Гривна, гривенник – десять копеек, алтын равнялся трем копейкам).

I способ.

(1200-120*9):(12-9)=40 (мужчин)

120-40=80 (женщин)

Ответ: 40 мужчин, 80 женщин.

II способ.

Пусть x мужчин, а женщин (120-х). Единица измерения – копейки.

Алгебраическое решение задачи приводит к уравнению

12х +(120 – х) * 9 = 1200.

х = 40, тогда 120- 40 = 80.

Ответ: 40 мужчин, 80 женщин.

Задачи с дробными числами

В XV – XVI столетиях учение о дробях приобретает уже знакомый нам теперь вид и оформляется приблизительно в те самые разделы, которые встречаются в наших учебниках.

Следует отметить, что раздел арифметики о дробях долгое время был одним из наиболее трудных. Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало – зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики.

В русских рукописных арифметиках XVII века дроби называли долями, позднее «ломаными числами». В старых руководствах находим следующие названия дробей на Руси:

1/2 – половина, полтина	1/3 – треть
1/4 – четь	1/6 – полтреть
1/8 - полчеть	1/12 –полполтреть
1/16 - полполчеть	1/24 – полполполтреть (малая треть)
1/32 – полполполчеть (малая четь)	1/5 – пятина
1/7 - седьмина	1/10 - десятина

В ходе развития математики было замечено, что самыми удобными для вычисления являются десятичные дроби. С XVII – XVIII в. они получили всеобщее распространение, особенно после создания и введения в большинстве стран метрической системы мер.

При сравнении дробей с одинаковыми знаменателями делили что-то целое на заданное количество частей и сравнивали нужное количество частей первой и второй дробей.

Что больше 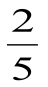или 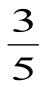? Делим пирог на 5 равных частей и видим, что две таких части меньше трёх таких же частей.

При сравнении дробей с одинаковыми числителями рассуждали так: чем на большее количество частей делим одно и тоже число, тем меньше получается дробь.
Но сравнивать приходилось и другие дроби не подходящие под эти правила. Сравнивать дроби, используя приём приведения дробей к общему знаменателю, люди научились гораздо позже, а до этого они пользовались многими другими способами, которые приводили их к верному результату.

1 способ: сравнение с половиной.

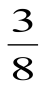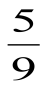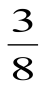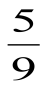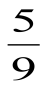Что больше или ? Если эти дроби сравнивать с , то меньше , а больше . Значит больше .

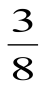2 способ: сравнение путём добавления до единицы.

Возьмём дроб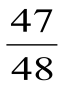и и 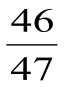. Первую дробь дополняем до единицы дробью 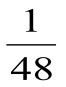, а вторую - 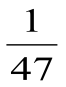. Но при сравнении дробей с одинаковыми числителями получаем, что 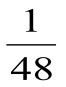меньше 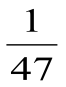, значит 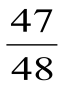больше .

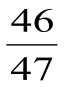3 способ: сравнение правильной и неправильной дробей: любая правильная дробь меньше неправильной дроби.

В различных книжных пособиях я нашла интересные задачи, которые были использованы в различные исторические периоды.

Задача Эйлера

Леонард Эйлер (4 апреля 1707г.- 18 сентября 1783г.) - является основателем русской научной математической школы. Полное собрание его сочинений насчитывает более 70 томов, а списки его трудов – более 850 названий.

Задача:Решив все свои сбережения поделить поровну между всеми сыновьями, некто составил завещание. «Старший из моих сыновей должен получить 1000 рублей и восьмую часть остатка; следующий – 2000 рублей и восьмую часть нового остатка; третий сын – 3000 рублей и восьмую часть следующего остатка и т.д.»

Вопрос:Определите число сыновей и размер завещанного сбережения.

Решение: так как все сыновья получили поровну, то восьмая часть каждого нового остатка была на 1000 рублей меньше восьмой части предыдущего остатка, а, значит, весь новый остаток был на 8000 рублей меньше предыдущего. Так как по условию, все деньги были поделены полностью, то, когда младший сын получил по завещанию, кроме нескольких тысяч рублей, ещё восьмую часть остатка, этого остатка не оказалось. Но тогда предыдущий остаток 8000 рублей. Из него предпоследний сын получил восьмую часть, равную 1000 рублей, а остальные 7000 рублей получил младший сын, который, таким образом, был седьмым сыном: сыновей было семь, а завещанная сумма 49000 рублей.

Задача Иоганна Хемелинга

Эту задачу более 200 лет назад задавал своим ученикам учитель математики Иоганн Хемелинг.

Задача:От числа одну восьмую

Взяв, прибавь ты к ней любую

Половину от трехсот,

И восьмушка превзойдёт

Не чуть-чуть – на пятьдесят

Три четвёртых. Буду рад,

Если тот, кто знает счёт,

Мне число то назовёт.

Решение: тот, кто знает счёт, составит уравнение

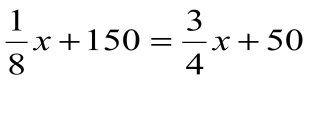
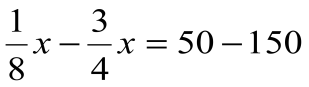
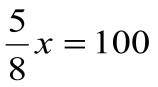
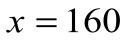
Ответ. 160.

Задача Диофанта

История сохранила нам мало черт биографии замечательного древнего математика Диофанта. Всё, что известно о нём, почерпнуто из надписи на его гробнице – надписи, составленной в форме математической задачи.
Задача:Путник! Здесь прах погребён Диофанта. И числа поведать могут, о чудо, сколь долог был век его жизни.

Часть шестую его представляло прекрасное детство.

Двенадцатая часть протекла ещё жизни – покрылся пухом тогда подбородок.Седьмую в бездетном браке провёл Диофант.

Прошло пятилетие; он был осчастливлен рожденьем прекрасного первенца сына.

Коему рок половину лишь жизни прекрасной и светлой дал на земле по сравненью с отцом.

И в печали глубокой старец земного удела конец восприял, переживши года четыре с тех пор, как сына лишился.

Скажи, сколько лет жизни достигнув, смерть восприял Диофант?

Решение: приняв всю жизнь Диофанта за х, можно составить уравнение

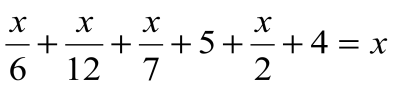
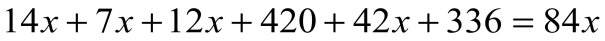
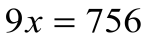
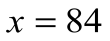
Значит, он женился в 21 год, стал отцом на 38 году, потерял сына на 80-м году и умер в 84 года.

Решить задачу с помощью счет.

Шли 7 старцев. У каждого старца по 7 костылей,

На каждом костыле по 7 сучков,

На каждом сучке по 7 кошелей,

В каждом кошеле по 7 пирогов,

В каждом пироге по 7 воробьев. Сколько всего?

Задача из “Счетной мудрости”

Идет корабль по морю, на нем мужеска полу и женска 120 человек. Найму дали 120 гривен, мущины дали по 4 алтына, а женщины дали по 3 алтына с человека. Сколько мужеска полу было и женска порознь? (Гривна, гривенник – десять копеек, алтын равнялся трем копейкам).

Задача Кирика Новгородца

Сколько месяцев, недель, дней и часов прожил человек, которому в 1136 г. Исполнилось 26 лет?

Задача из рукописи XVI века.

1.Собака усмотрела в 150 саженях зайца, который перебегает в 2 минуты по 500 сажен, а собака в 5 минут- 1300 сажен. Спрашивается, в какое время собака догонит зайца?

Скорость зайца - 500:2=250 саж./мин.
Скорость собаки - 1300:5=260 саж./мин.
Скорость приближения 260 - 250 =10 саж./мин.
150 : 10=15 мин - через 15 минут собака догонит зайца.

В работе рассмотрена задача, решаемая разными способами. Решение задач различными способами способствует углублению знаний, логического мышления, расширяет кругозор. Учащиеся начальных классов такие задачи в основном решают методом подбора или методом перебора. Лишь немалая часть решает алгебраическим способом с помощью составления уравнения.