Возврат значений из функции с помощью ссылочного типа

В этом случае ссылочный тип используется следующим образом:

· в заголовке функции параметры-результаты (в нашем примере y, z) записываем как переменные ссылочного типа, то есть с символом &;

· в тексте функции никакие дополнительные символы для этих переменных не используем, то есть работаем, как с обычными переменными;

· при вызове функции в качестве фактических параметров, указываем простые переменные соответствующего типа (cs, sn), объявленные обычным образом;

· входные параметры как параметры-значения используются по тем же правилам (см. §1);

· вызов функции с несколькими результатами осуществляется как вызов любой функции типа void, то есть отдельно, а не в выражении (см.§1).

Почему полученное значение возвращается в вызывающую функцию? С помощью ссылочного типа определяется другое имя ячейки. Поэтому для формального (y) и фактического (cs) параметров отводится одна и та же ячейка, которая в функции называется y, а при вызове в головной функции — cs. Поэтому если в функции получим y, то этим самым определим и значение cs, то есть полученное в функции значение возвращается в вызывающую функцию. Аналогичная ситуация имеет место для переменных z и sn.

Аналогично ссылочный тип используется и в случае, если значение переданной в функцию переменной надо изменить и это изменённое значение надо возвратить в точку вызова, то есть если одна и та же переменная является и входным, и выходным параметром. Например, составим функцию для перестановки значений двух переменных:

void CHANGE (float &u, float &v)

{ float temp;

temp=u; u=v; v=temp;

}

Тогда вызвать её можно, например, следующим образом:

float a=1.1, b=2.2;

CHANGE( a, b);

Так как a и u — это два имена одной и той же ячейки, то изменение u с 1.1 на 2.2 автоматически приведёт к изменению переменной a. Аналогично изменится и переменная b,если изменили значение переменной v. И тогда оператор cout<<a<<” “<<b; выведет изменённые значения 2.2 и 1.1, полученные в результате их перестановки.

Задачи и упражнения

1. Составить и проверить функцию, которая в текстовом режиме с помощью символов псевдографики рисует границу прямоугольника, не заполняя его внутреннюю область.

void ramka (int x0, int y0, int, int);

int main ()

{ ramka (2,5, 10, 30); getch(); return 0;

}

void ramka (int x0, int y0, int n1, int n2)

{ int x,y,i; x=x0; y=y0;

gotoxy(x,y++); printf("%c",218); // символ левого верхнего угла

for (i=0;i<n1-2;i++)

{ gotoxy(x,y++); printf("%c", 179); // для вертикальной линии

}

gotoxy(x++,y); printf("%c",192); // левый нижний угол

for (i=0;i<n2-2;i++)

{ gotoxy(x++,y); printf("%c",196); // для горизонтальной линии

}

gotoxy(x,y--); printf("%c",217); // правый нижний угол

for(i=0;i<n1-2;i++)

{ gotoxy(x,y--); printf("%c",179);

}

gotoxy(x--,y); printf("%c",191); // правый верхний угол

for(i=0;i<n2-2;i++)

{ gotoxy(x--,y); printf("%c",196);

}

}

Коды всех символов, в том числе и символов псевдографики, можно вывести с помощью следующей программы:

main()

{ clrscr(); textcolor(2);

for (int i=1; i<256; i++)

{ cprintf("%4d",i); printf("%c%c" , i, i%12?' ':'\n');

}

getch(); return 0;

}

Здесь по формату "%4d” выводим код символа указанным в textcolor вторым цветом, а по формату "%c” выводим символ с этим кодом цветом по умолчанию. При этом если i кратно 12, то выполняется переход на следующую строку экрана.

2. Составить функцию для нахождения действительных корней квадратного уравнения a∙x² + b∙x + c =0. Используя ее, составить и проверить функцию решения биквадратного уравнения a∙z⁴ + b∙z² + c =0.

3. Составить и проверить функцию решения линейного уравнения вида a∙x=b.

4. Вывести n параллельных горизонтальных линий разными цветами. Составить и использовать функцию для рисования одной горизонтальной линии.

5. Вывести n параллельных вертикальных линий разными цветами. Составить и использовать функцию для рисования одной вертикальной линии.

6. В текстовом режиме заполнить все окно вывода следующими фигурами, не заполняя их внутри:

a) ромбами;

б) равнобедренными треугольниками;

в) прямоугольными треугольниками с прямым углом внизу слева;

г) прямоугольными треугольниками с прямым углом внизу справа.

Составить и использовать функцию для рисования границы одной фигуры в зависимости от варианта.

7. В текстовом режиме нарисовать последовательность заполненных внутри прямоугольников, разместив их одним из следующих способов:

а) по диагонали окна, начиная с левого верхнего угла;

б) по диагонали окна, начиная с левого нижнего угла;

в) в шахматном порядке.

§ 3. Функции с одним результатом. Оператор return

Пример. Ввести последовательность целых чисел, пока не введём 0 (нуль). Для каждого из них найти и вывести сумму составляющих это число десятичных цифр.

При решении подобных задач с использованием функций необходимо ответить на следующие вопросы:

1) Какие функции, для каких целей будем составлять? Может быть несколько вариантов ответа на такой вопрос. Для определённости составим функцию для вычисления суммы десятичных цифр одного числа с именем SUMDIG. Эта функция будет вызываться в цикле несколько раз для каждого введённого числа.

2) Определяем входные и выходные параметры функции, то есть что для неё дано и что функция получает. У нас дано одно (!) целое число, а не массив, и получаем сумму его цифр, то есть тоже одно (!) целое число.

3) Составляем алгоритм функции SUMDIG и записываем его на языке C++. Для вычисления суммы цифр выделяем их в обратном порядке справа налево, используя получение остатка от деления на 10 (операция %) и целочисленное деление на 10 (операция /). Так как размерность числа может быть любой, то получается цикл с неизвестным количеством повторений. Получение цифр продолжаем, пока не получим при целочисленном делении нуль.

4) В головной функции в цикле вводим целое число, вызываем SUMDIG и выводим результат.

int SUMDIG(int );

int main()

{ int X=1; cout<< "For exit -- 0\n\n";

while (X)

{ cin>>X;

gotoxy(30, wherey()-1);

cout<<SUMDIG(X)<<endl;

}

return 0; }

int SUMDIG (int num)

{ int s=0, dig;

while (num)

{ dig=num%10;

s+=dig;

num/=10;

} return s;

}

В прототипе функции, возвращающей единственный результат, записываем его тип вместо void, имя функции и в скобках только входные параметры с их типами по тем же правилам, что и раньше. В скобках единственный выходной параметр не записывается. Аналогично записываем заголовок функции при её описании.

В тексте такой функции должен быть оператор вида

return выражение;

где выражение должно быть того же или совместимого типа, что и в заголовке функции.Оператор осуществляет выход из функции, передаёт управление в вызвавшую её функцию (в нашем примере в головную, но не обязательно) и возвращает в неё значение указанного выражения.

Особенности return:

· как частный случай выражения, можно возвращать константу или значение одной переменной;

· оператор может быть единственным в функции:

float MyFun1 (float x, float y)

{return x+y;

}

· наоборот, таких операторов может быть несколько и он не обязательно должен быть в конце функции. Но выполняется всегда один из них. Например, следующий вариант

float MyFun2A (float x, float y)

{ if (x>y) return x+y;

else return x*y;

}

короче, чем

float MyFun2B (float x, float y)

{ float r;

if (x>y) r= x+y;

else r= x*y;

return r;

}

Это же можно реализовать ещё компактнее с помощью тернарной операции:

float MyFun2 (float x, float y)

{ return x>y ? x+y : x*y;

}

· Оператор return обязателен, если возвращается одно значение, то есть в заголовке тип результата отличен от void.

Вызов такой функции с единственным возвращаемым значением записывается непосредственно в выражении, где используется её результат. Вызывать функцию, в том числе и типа void, можно не только из головной функции, но и из любой другой. Кроме “команды вывода”, обращение функции с одним результатом можно записать

· в операции присваивания, например sd=SUMDIG(1234);

· непосредственно в операторе if, не присваивая предварительно значение функции переменной (if (SUMDIG(a)>10)…), где a — переменная целого типа;

· в операторе while, например, while (SUMDIG(a*a)!=num)

или while (SUMDIG(a*a)-num)… и других операторах;

· при вызове другой функции в качестве фактического параметра, например, LINE2 (SUMDIG(a), 5, ‘.’); (см.1.1, пример2).

Оператор return имеет также и другое назначение. Он прекращает работу любой функции, в том числе и типа void. То есть он не обязательно должен иметь возвращаемое значение. Тогда return просто осуществляет выход из функции, не возвращая никакого значения. В таком виде, то есть в функции типа void, оператор return не обязателен. Если он не записан, то работа функции заканчивается после выполнения последнего оператора при достижении закрывающей скобки. В функции типа void оператор return имеет смысл использовать, если надо выйти из функции в разных её ветвях в зависимости от некоторого условия.

Задачи и упражнения

1. Вместо одной функции SINCOS (§ 2) cоставить и использовать две функции так, как было показано в § 3. Первая с именем MyCos вычисляет значение y, а вторая MySin — z, то есть каждая функция имеет один результат и должна использовать оператор return.Сравните вызов функций SINCOS, MyCos и MySin.

2. (Повторение). Изменить функцию SINCOS (§ 2) таким образом, чтобы оба результата, и y и z, вычислялись в одном цикле одновременно.

3. (Повторение). Изменить функцию SINCOS (§ 2), заменив оператор do … while на while.

4. (Повторение). Изменить функцию SINCOS (§ 2), заменив оператор do … while на for.

5. (Повторение). В функции main (см. 2.1) вместо оператора for записать while.

6. Для каждой пары введенных целых чисел найти их сумму и произведение двумя способами: с помощью одной функции типа void, которая возвращает и сумму, и произведение двух чисел; с помощью двух функций с одним результатом типа int, одна из которых возвращает сумму, а вторая — произведение двух целых чисел.

void SumMult (int, int, int &, int &);

int MySum (int, int );

int MyMult (int, int );

int main()

{ int a, b, r1, r2; cout<<endl<<" 0 0 -- exit"<<endl; cin>>a>>b;

while(a!=0 || b!=0 )

{ SumMult(a,b,r1,r2) ;

cout<<a<<" + "<<b<<" = "<<r1<<endl;

cout << a << " * " << b << " = " << r2 << endl;

cout << a << " + " << b << " = " << MySum (a,b) << endl;

cout << a << " * " << b << " = " << MyMult(a,b) << endl;

cin >> a >> b;

}

return 0; }

void SumMult ( int x, int y, int &s, int &p)

{ s=x+y; p=x*y;

}

int MySum (int x, int y)

{ return x+y;

}

int MyMult (int x, int y)

{ return x*y; }

7.Составить и использовать следующие функции: функцию типа int для нахождения наибольшего из двух чисел с помощью оператора if; функцию типа int для нахождения наибольшего из двух чисел с помощью тернарной операции; функцию типа void для нахождения наибольшего из двух чисел с помощью тернарной операции.

int maxfun1 (int, int);

int maxfun2 (int, int);

void maxfun3 (int , int , int &r);

int main()

{ long int a, b;

cout<<endl<<"Введите два числа; 0, 0 – выход : "<<endl;

cin>>a>>b;

while(a!=0 || b!=0 )

{ if (a==b)

cout<<endl<<a<<" is equal "<<b<<endl;

else { cout<<"max of "<<a<<" and "<<b<<"= "

<<maxfun1(a,b)<<" " <<maxfun2(a,b);

int mymax;

maxfun3(a,b,mymax); cout<<" "<<mymax<<endl;

}

cin>>a>>b;

}

return 0;

}

int maxfun1(int x,int y) // первый вариант

{ if (x>y) return x;

else return y;

}

int maxfun2(int x,int y) // второй вариант

{ return x>y?x:y; }

void maxfun3(int x,int y,int &r) //третий вариант

{ r=x>y?x:y;

}

8. Составить логическую функцию, которая определяет, принадлежит ли точка плоскости с координатами (x, y) части круга радиуса R, находящейся в первой или третьей четверти. Оси координат и окружность, ограничивающая указанные секторы, принадлежат области. В головной программе последовательно ввести координаты точек плоскости и для каждой из них вывести “Да” или “Нет” в зависимости от принадлежности точки указанной выше области.

bool Test(float, float, float); // или bool Test (float x, float y, float R);

main()

{ float X,Y, R;

do // ввод радиуса с контролем ввода

{ cout<<"R= "; cin>>R;

if (R<=0) cout<<"Radius must be positive, repeat\n ";

}

while (R<=0);

int gy; gy=wherey()+1;

cout<<"X=1000 && Y=1000 -- exit";

while (1)

{ gotoxy(2,gy); cin>>X; gotoxy(10,gy); cin>>Y;

if (X==1000 && Y==1000) break;

if (Test(X, Y, R)) { gotoxy(20, gy++); cout<<"Yes\n"; }

else { gotoxy(30, gy++); cout<<"No\n"; }

}

return 0;

}

bool Test (float x, float y, float r)

{ return x*x+y*y<=r*r && x*y>=0;

// или return x*x+y*y<=r*r && (x>=0 && y>=0 || x<=0 && y<=0);

// или if (x*x+y*y<=r*r && x*y>=0) return true; else return false;

}

9. Составить функцию, которая вычисляет значение бесконечной суммы ряда y = 1– 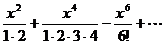c точностью e. В головной программе вычислить значения этой функции для x = –1.6, –1.4, –1.2, …, 1.4, 1.6 и вывести их на экран.

float MyCos(float x);

main()

{ printf("\n x MyCos(x) cos(x)");

for(float X=-1.6; X<=1.600001; X+=0.2)

printf("\n%6.1f%11.7f%11.7f", X, MyCos(X), cos(X));

/* Для контроля вывели также значение этой же суммы, вычисленное с помощью стандартной функции */

getch(); return 0;

}

float MyCos(float x)

{ float y=0, u=1, k=-1, eps=1e-6; // или eps=0.000001;

while (fabs(u)>eps)

{ y+=u; k+=2; u*=(-1)*x*x/(k*(k+1));

}

return y;

}

10. В одномерном целочисленном массиве найти числа с наибольшим количеством единиц в его двоичном представлении.

unsigned NUM (int);

main()

{ const n=5; long A[n]={10, 7, 14, 2, 19};

unsigned maxnum=0, num2;

for(int i=0; i<n; i++)

{ num2=NUM(A[i]);

if (num2>maxnum) maxnum = num2;

}

for(int i=0; i<n; i++)

if (NUM(A[i])==maxnum) cout<<A[i]<<" ";

getch(); return 0;

}

unsigned NUM (int a) // функция находит количество единиц

{ unsigned num=0; // в двоичном представлении одного целого числа

while (a)

{ num+=a%2; a/=2;

}

return num;

}

11. Составить и проверить функцию нахождения наименьшего общего кратного двух натуральных чисел.

12. Составить и проверить функцию нахождения наибольшего общего делителя двух натуральных чисел.

13. Составить и проверить функцию, которая переставляет цифры заданного целого числа N1 в обратном порядке и получает новое число N2. Например, если N1=425, то N2=524.

14. В массиве целых чисел найти количество чисел с наименьшим количеством цифр. Например, в массиве {123, 34, 56, 1000, 20, 55000, 777, 11} таких чисел 4, это 34, 56, 20, 11. Составить и использовать функцию, которая определяет количество цифр одного целого числа.

15. В целочисленном одномерном массиве все симметричные числа, т. е. числа, которые одинаково читаются слева направо и справа налево (палиндромы, перевертыши), заменить нулем. Составить и использовать логическую функцию для определения, является ли одно целое число симметричным.

16. В последовательности целых чисел (не в массиве) найти количество чисел, у которых в шестнадцатеричном представлении нет букв. Составить и использовать функцию для нахождения количества букв в шестнадцатеричном представлении одного целого числа.

17. В последовательности целых чисел (не в массиве) найти количество простых чисел. Составить и использовать логическую функцию для определения, является ли одно целое число простым.

18, 19. Среди заданных координатами вершин треугольников на плоскости найти треугольник с наименьшим периметром (площадью). Составить и использовать следующие функции: вычисление длины отрезка по координатам двух вершин; вычисление периметра (площади) одного треугольника; головную функцию, в которой находим координаты требуемого треугольника.

20, 21. Найти периметр (площадь) выпуклого многоугольника, если заданы координаты его вершин в порядке обхода. Составить и использовать следующие функции: вычисление длины отрезка по координатам двух вершин; вычисление периметра (площади) одного треугольника; головную функцию, в которой находим периметр (площадь) многоугольника.

§ 4. Одномерные массивы в функциях.
Сортировка массива

П р и м е р 1. Рассортировать одномерный целочисленный массив по возрастанию последней цифры числа. Если последняя цифра одинакова, то сортировать по возрастанию самого числа.

void MyInp(int x[],int size); // Ввод массива размерности size

void MyOut(int x[],int size); // Вывод массива размерности size

// Сортировка массива по возрастанию последней цифры числа void MySort(int x[],int size);

int DIGIT(int num) // Для одного числа получаем последнюю цифру

{ return abs(num % 10);

};

void RR(int &u, int &v) // Перестановка двух целых чисел

{ int t;

t=u; u=v; v=t;

};

// DIGIT и RR – это встраиваемые функции (см. 6.1).

int main()

{ const n=5; int A[n]; MyInp(A,n);

cout<<" Integer random array\n"; MyOut(A,n);

MySort(A,n);

cout<<" \n\Array after sorting\n"; MyOut(A,n);

getch(); return 0;

} ;

void MyInp(int x[],int size)

{ // или randomize();

for(int i=0; i<size; i++)

cin>>x[i]; // или x[i]=random(100)-50;

} ;

void MyOut(int x[],int size)

{ cout<<endl;

for(int i=0; i<size; i++)

cout<<x[i]<<" ";

} ;

Прежде чем писать последнюю функцию, рассмотрим следующий алгоритм сортировки одномерного массива. Последовательно сравниваем каждую пару двух соседних чисел и в зависимости от результата сравнения их переставляем или оставляем на месте. За один просмотр результата не достигнем, поэтому повторяем это. Алгоритм реализуется с помощью двух вложенных циклов.

В первом, плохом, варианте и внутренний, и внешний циклы можно повторить (size-1) раз, где size — размерность массива.

for ( int k=1; k<size; k++)

for(int j=0; j<size-1; j++)

if ( x[j]>x[j+1] )

RR(x[j], x[j+1]);

Улучшим внутренний цикл. Легко заметить, что после первого этапа наибольшее число массива будет в конце, то есть займёт своё место независимо от того, где оно было до сортировки. После второго шага второе наибольшее число займёт предпоследнее место, и так далее. Поэтому если вначале надо анализировать все пары чисел, то на втором шаге последнее число можем не “трогать”, так как оно уже на своём месте. Аналогично, на каждом последующем этапе количество сравниваемых пар можно на одну уменьшать. Тогда внутренний цикл будет таким:

for(int j=0; j<size-k; j++) …

Оптимизация внешнего цикла. Всегда ли надо (size-1) просмотров массива? Для “хорошего” массива, который частично рассортирован, результат можем получить и раньше. Как c учётом этого организовать внешний цикл? Предлагается следующее. Просмотр и анализ массива будем продолжать, если на предыдущем этапе была хотя бы одна перестановка. Если окажется, что ни одну пару не переставляли, то это означает, что массив рассортировали и можно выйти из внешнего цикла. Это реализуется с помощью переменной flag. Если на каком-то шаге была хотя бы одна перестановка, переменная flag изменит своё значение на единицу, и внешний цикл продолжаем. В противном случае, если не было ни одной перестановки, останется flag=0, и сортировка прекращается.

int flag=1, k; k=size;

while (flag)

{ k--; flag=0;

for(int j=0; j<k; j++)

if (x[j]>x[j+1]) { RR(x[j], x[j+1]);

flag=1;

}

}

Используемый при написании программы сортировки приём можно назвать методом последовательного (поэтапного) улучшения алгоритма (программы). Вначале составляем наиболее простой, не обязательно эффективный алгоритм. Его можем запрограммировать и отладить. При этом возможны, но не обязательны, некоторые упрощения постановки задачи. Отладив такой упрощённый вариант, улучшаем алгоритм и (или) программу и снимаем ограничения на условие задачи.

Если надо сортировать числовой массив по некоторому параметру числа, то в обычную сортировку необходимо внести следующие дополнения:

1) вначале строим массив параметров (массив D последних цифр);

2) сравниваем не сами числа, а эти параметры. И если параметры равны, только тогда сравниваем сами числа, если по условию требуется, как в нашем примере, “двойная” сортировка;

3) переставляем не только сами числа, но и их параметры, чтобы они соответствовали тем же числам, что и до сортировки.

void MySort(int x[],int size)

{ // Строим массив последних цифр

int D[20]; // 20 — наибольшая размерность

for(int i=0; i<size; i++)

D[i]=DIGIT(x[i]); /* В качестве фактического параметра функции можно использовать индексированную переменную, то есть элемент массива. В качестве формального параметра индексированную переменную записывать нельзя */

int flag=1, k; k=size;

while (flag)

{ k--; flag=0;

for(int j=0; j<k; j++)

// сравниваем параметры чисел, а если они равны, то и сами числа

if ( D[j]>D[j+1] || x[j]>x[j+1] && D[j]==D[j+1] )

{ RR(D[j], D[j+1]); // переставляем параметры

RR(x[j], x[j+1]); // переставляем исходные числа

flag=1;

}

} // the end of while

} ; // the end of function MySort

Независимо от того, является массив входным или выходным, он передаётся одинаково в качестве параметра функции по следующим правилам:

· в заголовке функции указываем тип элементов массива, его имя и пустые квадратные скобки. Чаще всего в качестве параметра указывается и его размерность (size в примере). Этим самым мы подчёркиваем, что работаем с массивом произвольной размерности;

· в тексте функции, как обычно, доступ к элементам массива осуществляется с помощью индексов;

· в вызывающей функции объявляем массив обычным образом;

· при вызове функции в качестве фактического параметра записываем только имя массива A (не A[I], не A[N], не A[], не A[5]) или &A[0] — адрес начала массива, т. е. номер первого байта элемента A[0].

При использовании массива в качестве параметра функции фактически передаётся не сам массив, а указательна него, или адрес массива, то есть номер первого байта первой ячейки массива (с индексом 0). Другими словами, int x[] (или int *x) в заголовке функции означает, что ячейка x предназначена для хранения адреса. При вызове функции из объявления int A[N] следует, что A, или &A[0], — это адрес начала массива из N элементов. Как и для простых переменных, этот адрес (но не сам массив) копируется в ячейку x. В результате получается, что в Aи в xхранятся адреса одной и той же области оперативной памяти. Или, другими словами, A[0] в main — это та же ячейка, что и x[0] в MySort, A[1] — это та же ячейка, что и x[1], и так далее. Поэтому если в функции массив x изменим, то этим самым мы изменим и массив A.

Независимо от того, массив является входным для функции, получается в нём, или одновременно входным и выходным, т. е. преобразуется в функции, массив вседа передаётся в функцию с помощью указателя. Никакого ссылочного типа для возврата массива из функции не требуется.

П р и м е р 2.

1) Составить функцию для ввода массива с контролем ввода, если разрешается вводить, например, только положительные числа. При вводе неположительных чисел выводим сообщение об ошибке, и программа должна дать возможность повторить ввод этого же элемента массива.

2) Составить функцию для вывода массива.

3) Составить логическую функцию, которая возвращает true или false в зависимости от того, рассортирован ли массив по возрастанию.

4) В main проверить эти функции.

void MyInp(int x[],int size);

void MyOut(int x[],int size);

bool Sorted(int x[],int size);

int main(int argc, char* argv[])

{ const n=5; int A[n]; MyInp(A,n);

cout<<" Integer array"; MyOut(A,n);

if (Sorted(A,n))

cout<<" \n рассортирован по возрастанию \n";

else cout<<" \n не рассортирован по возрастанию \n";

getch(); return 0;

} ;

void MyInp(int x[],int size)

{ for(int i=0; i<size; i++)

{ textcolor (15);

do // цикл для ввода одного числа с проверкой

{ cin>>x[i];

if (x[i]>0) break;

textcolor (12);

cprintf("Error. Repeat. ");

} while (1);

}

} ;

void MyOut(int x[], int size)

{ cout<<endl;

for(int i=0; i<size; i++) cout<<x[i]<<" ";

} ;

bool Sorted(int x[], int size)

{ for (int i=0; i<size-1; i++)

if (x[i]>x[i+1])

return false;

return true;

}

П р и м е р 3 (cтрока как массив символов).

Составить функцию, которая в строке находит количество цифр и количество введённого символа.

Для простой работы со строками достаточно объявить её как массив символов, не используя в явном виде указатели и возможности работы с ними (см. 2–й семестр). Объявление и инициализация строк были показаны в § 6 гл. 1. Для ввода строк вместо cin лучше использовать функцию gets, так как cin вводит строку до первого пробела.

void STRDIGIT (char t[],char simbol, int &K1, int &K2);

int main()

{ char str[50]; // объявляем массив наибольшей длины 50

gets(str); // ввод строки

char c1; int KDig, KC; cout<<"Input the symbol ";

c1=getchar(); // ввод одного символа

STRDIGIT(str,c1,KDig,KC);

cout<<"In the string ";

puts(str); // вывод строки, или printf ( “%s\n”, str)

cout<< KDig<< " digits and "<<KC << " of simbol "<<c1;

getch(); return 0;

}

void STRDIGIT (char t[], char simbol, int &K1, int &K2)

{ K1=0; K2=0;

for (int i=0; i<strlen(t); i++) // strlen возвращает длину строки

{ if (t[i]>='0' && t[i]<='9') K1++;

if (t[i]==simbol) K2++;

} }

// или

for (int i=0; t[i] !=’\0’; i++)

/* Цикл продолжается, пока не встретится символ конца строки, которым заканчивается любая строка. Это же можно записать короче: for (int i=0; t[i]; i++) */

{ if (isdigit(t[i])) K1++; // является ли символ цифрой

if ( ! (t[i]-simbol ) ) K2++; }

// или

for (int i=0; t[i];)

{ if ( isdigit(t[i])) K1++;

if (t[i++]==simbol) K2++;

}

Кроме функции getchar для ввода одного символа можно использовать функции getch или getche. От их выбора зависит, во-первых, надо ли при вводе символа нажимать не только на клавишу вводимого символа, но и на клавишу ввода (да, нет, нет) и, во-вторых, будет ли отображаться введённый символ на экране (да, нет, да).

Кроме функции isdigit, есть другие функции, анализирующие один символ:

· islower — является ли аргумент символом нижнего регистра (маленькой буквой, например);

· isupper — является ли аргумент символом верхнего регистра (большой буквой, например);

· isalpha — является ли аргумент буквой алфавита (верхнего или нижнего регистра);

· isgraph— является ли аргумент печатным символом, отличным от пробела;

· isprint — является ли аргумент печатным символом, включая пробел. Эти и другие подобные функции, имена которых начинаются с is, возвращают true или false в зависимости от того, принадлежит ли символ соответствующей группе.

Задачи и упражнения.

1. Задан массив точек плоскости, т. е. два одномерных массива одинаковой фиксированной размерности X[n] и Y[n], где (X_i, Y_i) — координаты i-й точки. Составить следующие функции:

1) логическую функцию Test для определения, принадлежит ли точка с координатами (x, y) k-й четверти;

2) функцию Num, которая с помощью первой функции в массиве точек определяет их количество в k-й четверти;

3) функцию main, которая с помощью второй функции находит количество точек в каждой четверти.

const n = 10;

bool Test (float , float , unsigned );

unsigned Num (float x[], float y[],unsigned k);

main()

{ float X[n]={1.1, 2.2, 3, 44, 0.5, -6.6, -0.7, -88, -9, -10},

Y[n]={11, 0.2, 33, 0.4,-5.5, 66, 77, -8.8,-9.9,-10};

cout<<" Number of points in\n";

for(unsigned K=1; K<=4;K++)

cout<<" "<<K<<" quarter "<<Num(X,Y,K)<<endl;

getch(); return 0;

}

bool Test (float u, float v, unsigned k)

{ switch (k)

{ case 1: return u>0 && v>0;

case 2: return u<0 && v>0;

case 3: return u<0 && v<0;

case 4: return u>0 && v<0;

}

}

unsigned Num (float x[], float y[], unsigned k)

{ unsigned number=0;

for (int i=0; i<n; i++)

if (Test (x[i], y[i], k)) number++;

return number;

}

2. В одномерном вещественном массиве найти среднее значение. Числа из отрезка [a, b] увеличить в 10 раз, а остальные оставить без изменения. Составить и использовать следующие функции: ввод массива; вывод массива; вычисление среднего значения элементов массива; изменение массива; функцию main для проверки названных функций.

void INP(float x[], int n);

void OU1(float x[], int n);

float AVER(float x[], int n);

void CHANGE(float a, float b, float x[], int n);

int main()

{ const N=5; float arr[N], a, b; INP(arr, N);

cout<<"Исходный массив"<<endl; OU1(arr, N);

cout<<"Среднее значение \t"<<AVER(arr, N)<<endl;

cout<<"a="; cin>>a; cout<<"b="; cin>>b;

CHANGE(a, b, arr, N);

cout<<"Измененный массив"<<endl; OU1(arr, N);

getch(); return 0;

}

void INP(float x[], int n)

{ for (int i=0; i<n; i++)

{ cout<<"enter "<<(i+1)<<" element of array -\t";

cin>>x[i]; clrscr();

}

}

void OU1(float x[], int n)

{ for (int i=0; i<n; i++)

cout<<(i+1)<<" element of array \t"<<x[i]<<endl;

}

float AVER(float x[], int n)

{ float s=0;

for (int i=0; i<n; i++, s+=x[i]);

s=s/n; return s; }

void CHANGE(float a,float b, float x[], int n)

{ for (int i=0; i<n; i++)

if(a<=x[i] && x[i]<=b)

x[i]*=10;

}

3. В одномерном целочисленном массиве найти, сколько раз повторяется наибольшее число, сколько раз повторяется наименьшее и вывести жёлтым цветом то из них, которое повторяется чаще. Например, в массиве {99, 8, 99, 99, 2} наибольшее число 99 повторяется чаще (три раза), чем наименьшее 2, которое встречается только один раз. Поэтому число 99 выделяем жёлтым цветом. Для другого массива {99, 7, 99, 7, 7} жёлтым цветом выделим число 7.

Составим и используем следующие функции: ввод массива (ReadArr); обычный, не “цветной” вывод массива (WriteArr); функцию ColorWriteArr, которая выводит число w массива цветом color1, остальные числа массива — цветом color2; поиск наиболь­шего и наименьшего элементов массива (MaxMin); функцию Num, котораяопределяет, сколько раз число w повторяется в массиве; main, проверяющую перечисленные выше функции.

void ReadArr(int [], int );

void WriteArr(int [], int );

void ColorWriteArr(int a[], int , int , int , int );

void MaxMin(int [], int , int &mx, int &mn);

int Num(int [], int , int );

main()

{ const n = 5; int a[5], MyMax, MyMin, num1, num2;

clrscr(); ReadArr(a, n);

WriteArr(a, n); MaxMin(a, n, MyMax, MyMin);

num1 = Num(a, n, MyMax); num2 = Num(a, n, MyMin);

cout<<"\nMyMax "<<MyMax<<" MyMin "<<MyMin<<endl;

cout<<"\nNumMax "<<num1<<" NumMin "<<num2<<endl;

if (num1>num2) ColorWriteArr(a, n, MyMax, 14, 11);

else if (num1<num2) ColorWriteArr(a, n, MyMin, 14, 11);

else cout<<" Number of max = number of min ";

getch(); return 0;

}

void ReadArr(int x[], int size)

{ for (int i=0; i<size; i++)

{ cout<<"a["<<i<<"]="; cin>>x[i];

}

}

void WriteArr(int x[], int size)

{ for (int i=0; i<size; i++) cout<<x[i]<<" ";

printf("\n");

}

void MaxMin(int x[], int size, int& mx, int& mn)

{ mx=x[0]; mn=x[0];

for (int i=0; i<size; i++)

if (x[i]<mn) mn = x[i];

else if (x[i]>mx) mx = x[i];

}

int Num(int x[], int size, int w)

{ int k=0;

for (int i=0; i<size; i++)

if (x[i] == w) k++;

return k;

}

void ColorWriteArr(int x[], int size, int w, int color1, int color2)

{ for (int i=0; i<size; i++)

{ if (x[i] == w) textcolor(color1);

else textcolor(color2);

cprintf("%5d ", x[i]);

}

printf("\n");

}

4. Запрограммировать в виде функции следующий алгоритм сортировки по убыванию. На первом шаге находим наибольший элемент всего массива, его номер k и переставляем x[0] c x[k]. На втором шаге находим наибольший элемент, начиная со второго элемента (с x[1]), его номер k и переставляем x[1] c x[k]. На третьем шаге находим наибольший элемент, начиная с третьего элемента (с x[2]), его номер k и переставляем x[2] c x[k]. Так продолжаем до конца массива.

5. Дан одномерный вещественный массив a[n]. Вычислить

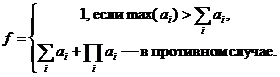
Вариант 1) Составить одну функцию типа void с тремя результатами, которая вычисляет наибольшее число массива, сумму всех его элементов и их произведение.

Вариант 2) Составить следующие три вещественные функции, каждая из которых имеет один результат: 1) вычисление наибольшего числа массива, 2) вычисление суммы всех его элементов, 3) нахождение их произведения.

В головной функции определить массив и с помощью одной или трех функций вычислить f.

6.Ввести два одномерных массива. В каждом из них найти наибольшее количество одинаковых подряд идущих элементов и этот элемент.

7.Ввести три одномерных массива — a[n],b[n],c[n]. Получить массив d[n] по формуле d=(a+b) ∙ (b+c), где сложение и умножение выполняются поэлементно. Составить и использовать следующие функции: для ввода массива, поэлементного сложения двух массивов, их поэлементного умножения, функцию main.

8.Рассортировать массив по возрастанию первых двух цифр числа. Составить и использовать следующие функции: для ввода массива, нахождения первой и второй цифры для одного целого числа, построения массива первых и вторых цифр, сортировки массивов, вывода массивов в виде таблицы, функцию main.

Замечание. В следующих задачах, как и в предыдущих, проект разбить на несколько функций.

9.Рассортировать массив следующим образом: сначала должны размещаться палиндромы по возрастанию их значений, а затем не палиндромы тоже по возрастанию их значений. Палиндром – это целое симметричное число, которое одинаково читается слева направо и справа налево.

10.Рассортировать целочисленный массив по убыванию следующих параметров числа:

a) количества единиц в двоичном представлении числа;

б) общего количества пар соседних различных цифр в двоичном представлении числа. Например, 25₁₀ = 11001₂ имеет две такие пары, а число 74₁₀ = 1001010₂ содержит пять таких пар;

в) количества букв в шестнадцатеричном представлении числа.

11.Массив точек плоскости рассортировать по убыванию первой координаты.

12.Даны массивы a[5], b[5], c[5]. Вычислить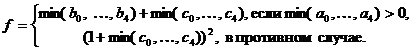

13.Даны два массива x[10] и y[10]. Построить третий массив z[10]:

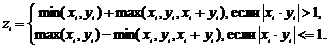
Составить и использовать следующие функции: вычисление наименьшего из двух чисел r = min(u, v); вычисление r = max(u, v); построение массива; функцию main().

§ 5. Область действия имён.
Локальные и глобальные имена

Так как в C++ нет вложенных функций, этот вопрос решается проще, чем на языке Pascal.

Есть несколько мест объявления переменных:

1) вне всех функций, в том числе вне main, например, в самом начале перед прототипами функций, между ними, перед функцией main или между текстами функций. Такие переменные, названные глобальными, “видны” из любой функции, размещенной после описания переменной, т. е. их можно там использовать. Память для глобальных переменных занята на всё время выполнения проекта;

2) в скобках в прототипе и в описании функции. Как видно из предыдущих примеров, не все исполь