Определение модуля продольной упругости для стали
1. ЦЕЛЬ РАБОТЫ
Изучить один из методов определения модуля продольной упругости Е для стали.
2. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Модуль упругости – величина, характеризующая упругие свойства материала. В случае малых деформаций, когда справедлив закон Гука, т.е. имеет место линейная зависимость между напряжениями и деформациями, модуль упругости представляет собой коэффициент пропорциональности.
Нормальному напряжению s, возникающему при простом растяжении (сжатии), соответствует в направлении растяжения модуль продольной упругости Е (модуль Юнга). Он равен отношению нормального напряжения s к относительному удлинению e, вызванному этим напряжением в направлении его действия
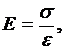 (1)
(1)
и характеризует способность материала сопротивляться растяжению (сжатию). Размерность модуля упругости Па, МПа.
Модуль упругости устанавливается экспериментально механическим испытанием образцов изучаемого материала. Он не является строго постоянной величиной для одного и того же материала, его значения меняются в зависимости от химического состава материала, от его предварительной обработки. Установлено, что модуль упругости слабо меняется с умеренным нагревом материала. Для стали это имеет место до температуры порядка 300…4000С. При более высоких температурах необходимо учитывать зависимиость модуля от температуры.
Предлагаемый метод модуля упругости заключается в сравнении значений деформаций балки, лежащей на двух опорах, определенных теоретически по формуле (7), приведенной в лаборатрной работе 3, и опытным путем на установке СМ4А, описание которой дано в лабораторной работе 1. Из полученого равенства определяют модуль упругости Е.
3. ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
1. Изобразить расчетную схему балки на двух опорах (рисунок) с сосредоточенной силой F в т.С, делящей балку пополам.
2. Определить изгибающий момент на участке АС.
3. Составить уравнения упругой линии балки на участке АС.
F yC 






 А C B
А C B
 |  | ||
 l/2
l/2
 l
l
Рис. Расчетная схема балки
4. Определить постоянные интегрирования из условий закрепления балки: при z=0 y=0, при z=l/2 y'=0.
5. Записать уравнения упругой линии балки на участке АС с учетом найденных значений интегрирования.
6. Выразить перемещение yc в точке С при нагрузке F=10 Н при неизвестном модуле упругости Е.
7. Установить индикатор для измерения прогибов балки в точке С лабораторной установки СМ4А.
8. Нагрузить балку в точке С начальной нагрузкой F=20 Н, показания индикатора установить на нуль.
9. Показания индикатора записать в таблицу.
| № п/п | FC, Н | ΔFC, Н | Показания индикатора  , мм , мм | Приращения прогиба 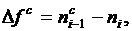 мм мм |
| 9,00 | - | |||
| Среднее значение | 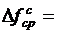 |
10.Давая одинаковые приращения нагрузке F = 10 Н, произвести три нагружения балки. Наибольшая суммарная нагрузка не должна превышать 50 Н. После каждого нагружения фиксировать показания индикатора и записывать в таблицу.
11.Определить среднее арифметическое приращение прогиба
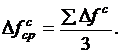
12.Приравнять значение прогиба 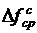 , определенного в п. 11, со значением перемещения ус (п. 6), определить модуль ЕОП и табличным (
, определенного в п. 11, со значением перемещения ус (п. 6), определить модуль ЕОП и табличным ( 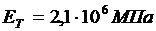 ) значениями модуля продольной упругости
) значениями модуля продольной упругости
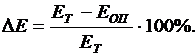
Допустимым считается отклонение в пределах 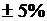 .
.
4. СОСТАВЛЕНИЕ ОТЧЕТА
Отчет о проделанной работе должен содержать: цель работы, схему опытной устаноовки и ее нагружение, таблицу с исходными данными и результатами опыта и расчеты по определению модуля упругости с сравнении с табличным значением модуля ЕТ.
5. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какое свойство материала характеризует модуль продольной упругости?
2. Какое допущение принимается при выводе приближенного дифференциального уравнения изогнутой оси балки?
3. Из каких условий определяются постоянные интегрирования дифференциального уравнения изогнутой оси балки?
4. О чем говорит гипотеза плоских сечений (гипотеза Бернулли)?
5. В каком случае имеет место чистый изгиб?
6. Краткое описание опытной установки.
Лабораторная работа 5
