Операции над нечеткими множествами

1. Дополнением нечеткого множества 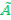, заданного на U, называется нечеткое множество 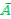с функцией принадлежности µ_A-(u) = 1 - µ_A(u) для всех u 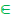U.

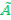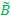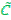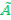
2. Пересечением нечетких множеств и , заданных на U, называется нечеткое множество = 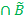с функцией принадлежности µ_C(u) = min (µ_A(u), µ_B(u)) для всех 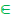u U.

3. Объединением нечетких множеств 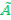и 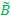, заданных на U, называется нечеткое множество D =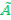 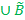с функцией принадлежности µ_D(u) = max (µ_A(u), µ_B(u)) для всех 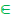u U.

Задача обучения без учителя, таксономия

Дано конечное множество М векторов размерности n.

Требуется разбить множество М на непересекающиеся подмножества (кластеры, таксоны), причем объекты, входящие в один кластер (таксон), должны быть достаточно близки друг к другу с точки зрения выбранного критерия близости ( расстояния), а элементы из разных кластеров (таксонов) должны быть достаточно далеки друг от друга.

Образ в ТА - таксон – множество объектов x, y, таких, что | x-y| < ρ

Постановка задачи поиска информативного пространства

Задача поиска информативных подсистем признаковсостоит в нахождении системы признаков (подпространства), в которой задача ДА решается достаточно качественно (с точки зрения того или иного критерия ).

Носитель

Носитель U – это универсальное множество

Например, если мы наблюдаем возраст занятых в определенных отраслях экономики, то носитель – это отрезок вещественной оси [16, 70], где единицей измерения выступают годы жизни человека.

Нечеткое множество А – это множество значений носителя, такое, что каждому значению носителя сопоставлена степень принадлежности этого значения множеству А.

Например: буквы латинского алфавита X, Y, Z безусловно принадлежат множеству Alphabet = {A, B, C, X, Y, Z}, и с этой точки зрения множество Alphabet –четкое. Но если анализировать множество «Оптимальный возраст работника», то возраст 50 лет принадлежит этому нечеткому множеству только с некоторой долей условности m, которую называют функцией принадлежности.

Функция принадлежности m_А(u) – это функция, областью определения которой является носитель U, u Î U, а областью значений – единичный интервал [0,1].

Чем выше m_А(u), тем выше оценивается степень принадлежности элемента носителя u нечеткому множеству А. Например [2.2], на рис. 2.2 представлена функция принадлежности нечеткого множества «Оптимальный возраст работающего», полученная на основании опроса ряда экспертов.

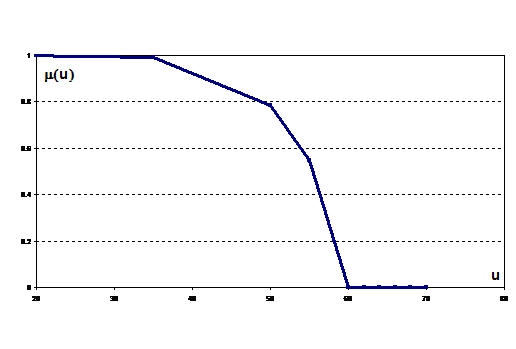
Рис. 2.2. Вид функции принадлежности

Видно что возраст от 20 до 35 оценивается экспертами как бесспорно оптимальный, а от 60 и выше – как бесспорно неоптимальный. В диапазоне от 35 до 60 эксперты проявляют неуверенность в своей классификации, и структура этой неуверенности как раз и передается графиком функции принадлежности.

Лингвистическая переменная

Заде определяет лингвистическую переменную так:

W = 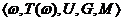, (2.1)

где w - название переменной, Т – терм-множество значений, т.е. совокупность ее лингвистических значений, U – носитель, G – синтаксическое правило, порождающее термы множества Т, М – семантическое правило, которое каждому лингвистическому значению w ставит в соответствие его смысл М(w), причем М(w) обозначает нечеткое подмножество носителя U.

К примеру, зададим лингвистическую переменную W = «Возраст работника».Определим синтаксическое правило G как определение «оптимальный», налагаемое на переменную W.Тогда полное терм-множество значений T = { T₁ = Оптимальный возраст работника, T₂ = Неоптимальный возраст работника }.Носителем U выступает отрезок [20, 70], измеряемый в годах человеческой жизни. И на этом носителе определены две функции принадлежности: для значения T₁ - m_T1(u), она изображена на рис. 2.2, для T₁ - m_T2(u), причем первая из них отвечает нечеткому подмножеству M₁, а вторая – M₂. Таким образом, конструктивное описание лингвистической переменной завершено.