Статистика, теоремы о вероятности

Классические вероятности

Статистика, теоремы о вероятностных событиях

Задание 9 № 315196

1.За­пи­сан рост (в сан­ти­мет­рах) пяти уча­щих­ся: 158, 166, 134, 130, 132. На сколь­ко от­ли­ча­ет­ся сред­нее ариф­ме­ти­че­ское этого на­бо­ра чисел от его ме­ди­а­ны?

Решение.

Медианой ряда, со­сто­я­ще­го из не­чет­но­го количества чисел, на­зы­ва­ет­ся число дан­но­го ряда, ко­то­рое окажется посередине, если этот ряд упорядочить. Ме­ди­а­ной ряда, со­сто­я­ще­го из чет­но­го количества чисел, на­зы­ва­ет­ся среднее ариф­ме­ти­че­ское двух сто­я­щих посередине чисел этого ряда.

Упорядочим дан­ный ряд: 130, 132, 134, 158, 166, следовательно, ме­ди­а­на равна 134. Сред­нее арифметическое же будет равно

Разница между ме­ди­а­ной и сред­ним арифметическим со­став­ля­ет 144 − 134 = 10.

Ответ: 10.

Ответ: 10

Источник: Банк заданий ФИПИ

Задание 9 № 316354

2.Фирма «Вспышка» из­го­тав­ли­ва­ет фонарики. Ве­ро­ят­ность того, что слу­чай­но вы­бран­ный фо­на­рик из пар­тии бракованный, равна 0,02. Ка­ко­ва ве­ро­ят­ность того, что два слу­чай­но вы­бран­ных из одной пар­тии фо­на­ри­ка ока­жут­ся небракованными?

Решение.

Вероятность того, что один слу­чай­но вы­бран­ный из пар­тии фо­на­рик — небракованный, со­став­ля­ет 1 − 0,02=0,98. Ве­ро­ят­ность того, что мы вы­бе­рем од­но­вре­мен­но два не­бра­ко­ван­ных фо­на­ри­ка равна 0,98 · 0,98 = 0,9604.

Ответ: 0,9604

0,9604

Источник: МИОО: Тре­ни­ро­воч­ная работа по ма­те­ма­ти­ке 19.02.2014 ва­ри­ант МА90501.

Задание 9 № 325288

3.Сред­ний рост жи­те­ля го­ро­да, в ко­то­ром живет Даша, равен 170 см. Рост Даши 173 см. Какое из сле­ду­ю­щих утвер­жде­ний верно?

1) Даша — самая вы­со­кая де­вуш­ка в го­ро­де.

2) Обя­за­тель­но най­дет­ся де­вуш­ка ниже 170 см.

3) Обя­за­тель­но най­дет­ся че­ло­век ро­стом менее 171 см.

4) Обя­за­тель­но най­дет­ся че­ло­век ро­стом 167 см.

Решение.

Первое утвер­жде­ние неверно: например, в го­ро­де могут жить три де­вуш­ки ро­стом 162 см, 173 см и и 175 см.

Второе утвер­жде­ние неверно: в го­ро­де может жить толь­ко одна де­вуш­ка — Даша.

Третье утвер­жде­ние верно: если все жи­те­ли будут не ниже 171 см, то сред­ний рост будет не мень­ше 171 см.

Четвёртое утвер­жде­ние неверно: например, в го­ро­де могут жить трое жи­те­лей ро­стом 165 см, 172 см и 173 см.

Ответ: 3.

Ответ: 3

Задание 9 № 325454

4.Из­вест­но, что в не­ко­то­ром ре­ги­о­не ве­ро­ят­ность того, что ро­див­ший­ся мла­де­нец ока­жет­ся маль­чи­ком, равна 0,512. В 2010 г. в этом ре­ги­о­не на 1000 ро­див­ших­ся мла­ден­цев в сред­нем при­ш­лось 477 де­во­чек. На­сколь­ко ча­сто­та рож­де­ния де­воч­ек в 2010 г. в этом ре­ги­о­не от­ли­ча­ет­ся от ве­ро­ят­но­сти этого со­бы­тия?

Решение.

Частота cобытия «рождение девочки» равна 477 : 1000 = 0,477. Ве­ро­ят­ность рождения де­воч­ки в этом ре­ги­о­не равна 1 − 0,512 = 0,488. По­это­му частота дан­но­го события от­ли­ча­ет­ся от его ве­ро­ят­но­сти на 0,488 − 0,477 = 0,011.

Ответ: 0,011.

Ответ: 0,011

0,011

Задание 9 № 325457

5.Ве­ро­ят­ность того, что новая ша­ри­ко­вая ручка пишет плохо (или не пишет), равна 0,19. По­ку­па­тель в ма­га­зи­не вы­би­ра­ет одну такую ручку. Най­ди­те ве­ро­ят­ность того, что эта ручка пишет хо­ро­шо.

Решение.

Вероятность того, что ручка пишет хо­ро­шо равна 1 − 0,19 = 0,81.

Ответ: 0,81.

Ответ: 0,81

0,81

Источник: Банк заданий ФИПИ

Задание 9 № 340463

6.На эк­за­ме­не по гео­мет­рии школь­ни­ку достаётся одна за­да­ча из сбор­ни­ка. Ве­ро­ят­ность того, что эта за­да­ча по теме «Углы», равна 0,1. Ве­ро­ят­ность того, что это ока­жет­ся за­да­ча по теме «Па­рал­ле­ло­грамм», равна 0,6. В сбор­ни­ке нет задач, ко­то­рые од­но­вре­мен­но от­но­сят­ся к этим двум темам. Най­ди­те ве­ро­ят­ность того, что на эк­за­ме­не школь­ни­ку до­ста­нет­ся за­да­ча по одной из этих двух тем.

Решение.

Суммарная ве­ро­ят­ность несовместных со­бы­тий равна сумме ве­ро­ят­но­стей этих событий: P=0,6 + 0,1 = 0,7.

Ответ: 0,7.

Ответ: 0,7

0,7

Задание 9 № 341364

7.Игральную кость бро­са­ют дважды. Най­ди­те ве­ро­ят­ность того, что сумма двух вы­пав­ших чисел равна 4 или 7.

Классические вероятности

Задание 9 № 149

1.На экзамене 25 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет.

Решение.

Сергей выучил 25 − 3 = 22 вопроса. Поэтому вероятность того, что ему попадётся выученный билет равна

Ответ: 0,88.

Ответ: 0,88

0,88

Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1313.

Задание 9 № 175

2.На эк­за­ме­не 25 билетов, Сер­гей не вы­учил 3 из них. Най­ди­те ве­ро­ят­ность того, что ему попадётся вы­учен­ный билет.

Решение.

Вероятность бла­го­при­ят­но­го случая( ) — от­но­ше­ние ко­ли­че­ства бла­го­при­ят­ных слу­ча­ев к ко­ли­че­ству всех случаев. В дан­ной за­да­че бла­го­при­ят­ным слу­ча­ем яв­ля­ет­ся взя­тие на эк­за­ме­не вы­учен­но­го билета. Всего бла­го­при­ят­ных слу­ча­ев 22(25−3), а ко­ли­че­ство всех слу­ча­ев 25. От­но­ше­ние со­от­вет­ствен­но равно

Ответ: 0,88.

Ответ: 0,88

0,88

Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1317.

Задание 9 № 132728

3.Коля вы­би­ра­ет трех­знач­ное число. Най­ди­те ве­ро­ят­ность того, что оно де­лит­ся на 5.

Решение.

Всего трех­знач­ных чисел 900. На пять де­лит­ся каж­дое пятое их них, то есть таких чисел Ве­ро­ят­ность того, что Коля вы­брал трех­знач­ное число, де­ля­ще­е­ся на 5, опре­де­ля­ет­ся от­но­ше­ни­ем ко­ли­че­ства трех­знач­ных чисел, де­ля­щих­ся на 5, ко всему ко­ли­че­ству трех­знач­ных чисел:

Ответ: 0,2.

Примечание.

Количества чисел можно было не находить: ис­ко­мая ве­ро­ят­ность равна одной пятой потому, что пятая часть чисел де­лит­ся на 5.

Ответ: 0,2

0,2

Задание 9 № 132730

4.Телевизор у Маши сло­мал­ся и по­ка­зы­ва­ет толь­ко один слу­чай­ный канал. Маша вклю­ча­ет телевизор. В это время по трем ка­на­лам из два­дца­ти по­ка­зы­ва­ют кинокомедии. Най­ди­те ве­ро­ят­ность того, что Маша по­па­дет на канал, где ко­ме­дия не идет.

Решение.

Количество каналов, по ко­то­рым не идет ки­но­ко­ме­дий Ве­ро­ят­ность того, что Маша не по­па­дет на канал, по ко­то­ро­му идут ки­но­ко­ме­дии равна от­но­ше­нию ко­ли­че­ства каналов, по ко­то­рым не идут ки­но­ко­ме­дии к об­ще­му числу каналов:

Ответ: 0,85.

Ответ: 0,85

0,85

Задание 9 № 132732

5.На та­рел­ке 12 пирожков: 5 с мясом, 4 с ка­пу­стой и 3 с вишней. На­та­ша на­у­гад вы­би­ра­ет один пирожок. Най­ди­те ве­ро­ят­ность того, что он ока­жет­ся с вишней.

Решение.

Вероятность того, что будет вы­бран пи­ро­жок с виш­ней равна от­но­ше­нию ко­ли­че­ства пи­рож­ков с виш­ней к об­ще­му ко­ли­че­ству пирожков:

Ответ:0,25

Ответ: 0,25

0,25

Задание 9 № 132734

6.В фирме такси в дан­ный мо­мент сво­бод­но 20 машин: 9 черных, 4 жел­тых и 7 зеленых. По вы­зо­ву вы­еха­ла одна из машин, слу­чай­но ока­зав­ша­я­ся ближе всего к заказчику. Най­ди­те ве­ро­ят­ность того, что к нему при­е­дет жел­тое такси.

Решение.

Вероятность того, что при­е­дет жел­тая ма­ши­на равна от­но­ше­нию ко­ли­че­ства жел­тых машин к об­ще­му ко­ли­че­ству машин:

Ответ: 0,2.

Ответ: 0,2

0,2

Задание 9 № 132736

7.В каж­дой де­ся­той банке кофе со­глас­но усло­ви­ям акции есть приз. Призы рас­пре­де­ле­ны по бан­кам случайно. Варя по­ку­па­ет банку кофе в на­деж­де вы­иг­рать приз. Най­ди­те ве­ро­ят­ность того, что Варя не най­дет приз в своей банке.

Решение.

Так как в каж­дой де­ся­той банке кофе есть приз, то ве­ро­ят­ность вы­иг­рать приз равна Поэтому, ве­ро­ят­ность не вы­иг­рать приз равна

Ответ:0,9.

Ответ: 0,9

0,9

Задание 9 № 132738

8.Миша с папой ре­ши­ли по­ка­тать­ся на ко­ле­се обозрения. Всего на ко­ле­се два­дцать че­ты­ре кабинки, из них 5 — синие, 7 — зеленые, остальные — красные. Ка­бин­ки по оче­ре­ди под­хо­дят к плат­фор­ме для посадки. Най­ди­те ве­ро­ят­ность того, что Миша про­ка­тит­ся в крас­ной кабинке.

Решение.

Вероятность того, что по­дой­дет крас­ная ка­бин­ка равна от­но­ше­нию ко­ли­че­ства крас­ных ка­би­нок к об­ще­му ко­ли­че­ству ка­би­нок на ко­ле­се обозрения. Всего крас­ных кабинок: По­это­му ис­ко­мая ве­ро­ят­ность

Ответ: 0,5.

Ответ: 0,5

0,5

Задание 9 № 132740

9.У ба­буш­ки 20 чашек: 5 с крас­ны­ми цветами, осталь­ные с синими. Ба­буш­ка на­ли­ва­ет чай в слу­чай­но вы­бран­ную чашку. Най­ди­те ве­ро­ят­ность того, что это будет чашка с си­ни­ми цветами.

Решение.

Вероятность того, что чай на­льют в чашку с си­ни­ми цве­та­ми равна от­но­ше­нию ко­ли­че­ства чашек с си­ни­ми цве­та­ми к об­ще­му ко­ли­че­ству чашек. Всего чашек с си­ни­ми цветами: По­это­му ис­ко­мая ве­ро­ят­ность

Ответ: 0,75.

Ответ: 0,75

0,75

Задание 9 № 132744

10.Родительский ко­ми­тет за­ку­пил 25 паз­лов для по­дар­ков детям на окон­ча­ние года, из них 15 с ма­ши­на­ми и 10 с ви­да­ми городов. По­дар­ки рас­пре­де­ля­ют­ся слу­чай­ным образом. Най­ди­те ве­ро­ят­ность того, что Толе до­ста­нет­ся пазл с машиной.

Решение.

Вероятность по­лу­чить пазл с ма­ши­ной равна от­но­ше­нию числа паз­лов с ма­ши­ной к об­ще­му числу за­куп­лен­ных пазлов, то есть .

Ответ: 0,6.

Ответ: 0,6

0,6

Задание 9 № 132748

11.В сред­нем из каж­дых 80 по­сту­пив­ших в про­да­жу ак­ку­му­ля­то­ров 76 ак­ку­му­ля­то­ров заряжены. Най­ди­те ве­ро­ят­ность того, что куп­лен­ный ак­ку­му­ля­тор не заряжен.

Решение.

Из каж­дых 80 ак­ку­му­ля­то­ров в сред­нем будет 80 − 76 = 4 незаряженных. Таким образом, ве­ро­ят­ность ку­пить не­за­ря­жен­ный ак­ку­му­ля­тор равна доле числа не­за­ря­жен­ных ак­ку­му­ля­то­ров из каж­дых 80 купленных, то есть .

Ответ: 0,05.

Ответ: 0,05

0,05

Задание 9 № 311324

12.Для эк­за­ме­на под­го­то­ви­ли би­ле­ты с но­ме­ра­ми от 1 до 50. Ка­ко­ва ве­ро­ят­ность того, что на­у­гад взя­тый уче­ни­ком билет имеет од­но­знач­ный номер?

Решение.

Всего было под­го­тов­ле­но 50 билетов. Среди них 9 были однозначными. Таким об­ра­зом ве­ро­ят­ность того, что на­у­гад взя­тый уче­ни­ком билет имеет од­но­знач­ный номер равна

Ответ: 0,18

0,18

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 1)

Задание 9 № 311336

13.В мешке со­дер­жат­ся же­то­ны с но­ме­ра­ми от 5 до 54 включительно. Ка­ко­ва вероятность, того, что из­вле­чен­ный на­у­гад из мешка жетон со­дер­жит дву­знач­ное число?

Решение.

Всего в мешке же­то­нов - 50. Среди них 45 имеют дву­знач­ный номер. Таким образом, вероятность, того, что из­вле­чен­ный на­у­гад из мешка жетон со­дер­жит дву­знач­ное число равна

Ответ: 0,9

0,9

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 2)

Задание 9 № 311359

14.В денежно-вещевой ло­те­рее на 100 000 би­ле­тов разыг­ры­ва­ет­ся 1300 ве­ще­вых и 850 де­неж­ных выигрышей. Ка­ко­ва ве­ро­ят­ность по­лу­чить ве­ще­вой выигрыш?

Решение.

Вероятность по­лу­чить ве­ще­вой вы­иг­рыш равна от­но­ше­нию ко­ли­че­ства ве­ще­вых вый­гра­шей к об­ще­му ко­ли­че­ству выйгрышей

Ответ: 0,013

0,013

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 4)

Задание 9 № 311415

15.Из 900 новых флеш-карт в сред­нем 54 не при­год­ны для записи. Ка­ко­ва ве­ро­ят­ность того, что слу­чай­но вы­бран­ная флеш-карта при­год­на для записи?

Решение.

Из 900 карт ис­прав­ны 900 − 54 = 846 шт. По­это­му ве­ро­ят­ность того, что слу­чай­но вы­бран­ная флеш-карта при­год­на для за­пи­си равна:

.

Ответ: 0,94.

Ответ: 0,94

0,94

Источник: ГИА-2013. Математика. Тренировочная работа № 1 (1 вар.)

Задание 9 № 311505

16.В чем­пи­о­на­те по фут­бо­лу участ­ву­ют 16 команд, ко­то­рые же­ре­бьев­кой рас­пре­де­ля­ют­ся на 4 группы: A, B, C и D. Ка­ко­ва ве­ро­ят­ность того, что ко­ман­да Рос­сии не по­па­да­ет в груп­пу A?

Решение.

Каждая ко­ман­да по­па­дет в груп­пу с ве­ро­ят­но­стью 0,25. Таким образом, ве­ро­ят­ность того, что ко­ман­да не по­па­да­ет в груп­пу равна 1-0,25=0,75.

Ответ: 0,75

0,75

Источник: ГИА-2012. Математика. Диагностическая работа № 2(1вар)

Задание 9 № 311512

17.В груп­пе из 20 рос­сий­ских ту­ри­стов не­сколь­ко че­ло­век вла­де­ют ино­стран­ны­ми языками. Из них пя­те­ро го­во­рят толь­ко по-английски, трое толь­ко по-французски, двое по-французски и по-английски. Ка­ко­ва ве­ро­ят­ность того, что слу­чай­но вы­бран­ный ту­рист го­во­рит по-французски?

Решение.

Количество туристов, го­во­ря­щих по-французски, равно 5. По­это­му ве­ро­ят­ность того, что слу­чай­но вы­бран­ный ту­рист го­во­рит по-французски равна

Ответ: 0,25

0,25

Источник: ГИА-2012. Математика. Диагностическая работа №2 (5 вар)

Задание 9 № 311525

18.В ко­роб­ке 14 па­ке­ти­ков с чёрным чаем и 6 па­ке­ти­ков с зелёным чаем. Павел на­у­гад вы­ни­ма­ет один пакетик. Ка­ко­ва ве­ро­ят­ность того, что это па­ке­тик с зелёным чаем?

Решение.

Всего в ко­роб­ке 14+6=20 пакетиков. Ве­ро­ят­ность того, что Павел вы­та­щит па­ке­тик с зелёным чаем равна

Ответ: 0,3

0,3

Источник: ГИА-2012. Математика. Тренировочная работа № 3 (1 вар)

Задание 9 № 311767

19.Стас, Денис, Костя, Маша, Дима бро­си­ли жре­бий — кому на­чи­нать игру. Най­ди­те ве­ро­ят­ность того, что на­чи­нать игру долж­на будет девочка.

Решение.

Вероятность со­бы­тия равна от­но­ше­нию ко­ли­че­ства бла­го­при­ят­ных слу­ча­ев к ко­ли­че­ству всех случаев. Среди пяти детей одна девочка. По­это­му ве­ро­ят­ность равна

Ответ: 0,2.

Ответ: 0,2

0,2

Источник: МИОО: Ди­а­гно­сти­че­ская работа по ма­те­ма­ти­ке 01.10.2013 ва­ри­ант МА90101.

Задание 9 № 311919

20.Перед на­ча­лом фут­боль­но­го матча судья бро­са­ет монетку, чтобы определить, какая из ко­манд будет пер­вой вла­деть мячом. Ко­ман­да А долж­на сыг­рать два матча — с ко­ман­дой В и с ко­ман­дой С. Най­ди­те ве­ро­ят­ность того, что в обоих мат­чах пер­вой мячом будет вла­деть ко­ман­да А.

Решение.

Рассмотрим все воз­мож­ные ис­хо­ды жеребьёвки.

· Команда А в матче в обоих мат­чах пер­вой вла­де­ет мячом.

· Команда А в матче в обоих мат­чах не вла­де­ет мячом первой.

· Команда А в матче с ко­ман­дой В вла­де­ет мячом первой, а в матче с ко­ман­дой С — второй.

· Команда А в матче с ко­ман­дой С вла­де­ет мячом первой, а в матче с ко­ман­дой В — второй.

Из че­ты­рех ис­хо­дов один яв­ля­ет­ся благоприятным, ве­ро­ят­ность его на­ступ­ле­ния равна 0,25.

Ответ: 0,25.

Ответ: 0,25

0,25

Источник: МИОО: Тре­ни­ро­воч­ная работа по ма­те­ма­ти­ке 19.11.2013 ва­ри­ант МА90201.

Задание 9 № 315159

21.В лыж­ных гон­ках участ­ву­ют 11 спортс­ме­нов из Рос­сии, 6 спортс­ме­нов из Нор­ве­гии и 3 спортс­ме­на из Шве­ции. По­ря­док, в ко­то­ром спортс­ме­ны стар­ту­ют, опре­де­ля­ет­ся жре­би­ем. Най­ди­те ве­ро­ят­ность того, что пер­вым будет стар­то­вать спортс­мен из Рос­сии.

Решение.

Всего спортс­ме­нов 11 + 6 + 3 = 20 человек. По­это­му ве­ро­ят­ность того, что пер­вым будет стар­то­вать спортс­мен из Рос­сии равна

Ответ: 0,55.

Ответ: 0,55

0,55

Источник: Банк заданий ФИПИ

Задание 9 № 315173

22.В лыж­ных гон­ках участ­ву­ют 11 спортс­ме­нов из Рос­сии, 6 спортс­ме­нов из Нор­ве­гии и 3 спортс­ме­на из Шве­ции. По­ря­док, в ко­то­ром спортс­ме­ны стар­ту­ют, опре­де­ля­ет­ся жре­би­ем. Най­ди­те ве­ро­ят­ность того, что пер­вым будет стар­то­вать спортс­мен не из Рос­сии.

Решение.

Всего спортс­ме­нов 11 + 6 + 3 = 20 человек. По­это­му ве­ро­ят­ность того, что пер­вым будет стар­то­вать спортс­мен не из Рос­сии равна

Ответ: 0,45.

Ответ: 0,45

0,45

Источник: Банк заданий ФИПИ

Задание 9 № 315195

23.Из каж­дых 1000 элек­три­че­ских лам­по­чек 5 бракованных. Ка­ко­ва ве­ро­ят­ность ку­пить ис­прав­ную лампочку?

Решение.

Ве­ро­ят­ность ку­пить ис­прав­ную лам­поч­ку равна доле ис­прав­ных лам­по­чек в общем количестве лампочек:

Ответ: 0,995.

Ответ: 0,995

0,995

Источник: Банк заданий ФИПИ

Задание 9 № 316328

24.Петя, Вика, Катя, Игорь, Антон, По­ли­на бро­си­ли жре­бий — кому на­чи­нать игру. Най­ди­те ве­ро­ят­ность того, что на­чи­нать игру дол­жен будет мальчик.

Решение.

Вероятность со­бы­тия равна от­но­ше­нию ко­ли­че­ства бла­го­при­ят­ных слу­ча­ев к ко­ли­че­ству всех случаев. Бла­го­при­ят­ными слу­ча­ями яв­ля­ют­ся 3 случая, когда игру на­чи­на­ет Петя, Игорь или Антон, а ко­ли­че­ство всех слу­ча­ев 6. По­это­му ис­ко­мое от­но­ше­ние равно

Ответ: 0,5.

Ответ: 0,5

0,5

Источник: МИОО: Ди­а­гно­сти­че­ская работа по ма­те­ма­ти­ке 01.10.2013 ва­ри­ант МА90103.

Задание 9 № 325436

25.Из 1600 па­ке­тов мо­ло­ка в сред­нем 80 про­те­ка­ют. Ка­ко­ва ве­ро­ят­ность того, что слу­чай­но вы­бран­ный пакет мо­ло­ка не течёт?

Решение.

Вероятность того, что пакет мо­ло­ка про­те­ка­ет равна По­это­му ве­ро­ят­ность того, что слу­чай­но вы­бран­ный пакет мо­ло­ка не течёт равна

Ответ: 0,95.

Ответ: 0,95

0,95

Задание 9 № 325450

26.В со­рев­но­ва­ни­ях по ху­до­же­ствен­ной гим­на­сти­ке участ­ву­ют три гим­наст­ки из Рос­сии, три гим­наст­ки из Укра­и­ны и че­ты­ре гим­наст­ки из Бе­ло­рус­сии. По­ря­док вы­ступ­ле­ний опре­де­ля­ет­ся же­ребьёвкой. Най­ди­те ве­ро­ят­ность того, что пер­вой будет вы­сту­пать гим­наст­ка из Рос­сии.

Решение.

Всего в со­рев­но­ва­ни­ях участ­ву­ют 3 + 3 + 4 = 10 гимнасток. По­это­му ве­ро­ят­ность того, что пер­вой будет будет вы­сту­пать гим­наст­ка из Рос­сии равна

Ответ: 0,3.

Ответ: 0,3

0,3

Задание 9 № 325453

27.Опре­де­ли­те ве­ро­ят­ность того, что при бро­са­нии иг­раль­но­го ку­би­ка (пра­виль­ной кости) вы­па­дет не­чет­ное число очков.

Решение.

При бро­са­нии ку­би­ка рав­но­воз­мож­ны шесть раз­лич­ных исходов. Со­бы­тию "выпадет нечётное число очков" удо­вле­тво­ря­ют три случая: когда на ку­би­ке вы­па­да­ет 1, 3 или 5 очков. По­это­му ве­ро­ят­ность того, что на ку­би­ке вы­па­дет нечётное число очков равна

Ответ: 0,5.

Ответ: 0,5

0,5

Задание 9 № 325481

28.Опре­де­ли­те ве­ро­ят­ность того, что при бро­са­нии ку­би­ка вы­па­ло число очков, не боль­шее 3.

Решение.

При бро­са­нии ку­би­ка рав­но­воз­мож­ны шесть раз­лич­ных исходов. Со­бы­тию "выпадет не боль­ше трёх очков" удо­вле­тво­ря­ют три случая: когда на ку­би­ке вы­па­да­ет 1, 2, или 3 очка. По­это­му ве­ро­ят­ность того, что на ку­би­ке вы­па­дет не боль­ше трёх очков равна

Ответ: 0,5.

Ответ: 0,5

0,5

Задание 9 № 325482

29.В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют два­жды. Най­ди­те ве­ро­ят­ность того, что орел вы­па­дет ровно 1 раз.

Решение.

Всего воз­мож­ны че­ты­ре исхода: решка-решка, решка-орёл, орёл-решка, орёл-орёл. Орёл вы­па­да­ет ровно один раз в двух случаях, по­это­му ве­ро­ят­ность того, что орёл вы­па­дет ровно один раз равна

Ответ: 0,5.

Ответ: 0,5

0,5

Задание 9 № 325491

30.Иг­раль­ную кость бро­са­ют два­жды. Най­ди­те ве­ро­ят­ность того, что оба раза вы­па­ло число, боль­шее 3.

Решение.

При бро­са­нии ку­би­ка рав­но­воз­мож­ны шесть раз­лич­ных исходов. Со­бы­тию "выпадет боль­ше трёх очков" удо­вле­тво­ря­ют три случая: когда на ку­би­ке вы­па­да­ет 4, 5, или 6 очков. По­это­му ве­ро­ят­ность того, что на ку­би­ке вы­па­дет не боль­ше трёх очков равна Таким образом, при одном бро­са­нии ку­би­ка с оди­на­ко­вой ве­ро­ят­но­стью ре­а­ли­зу­ет­ся либо со­бы­тие А — вы­па­ло число, боль­шее 3, либо со­бы­тие Б — вы­па­ло число не боль­ше 3. То есть рав­но­ве­ро­ят­но реализуются че­ты­ре события: А-А, А-Б, Б-А, Б-Б. По­это­му ве­ро­ят­ность того, что оба раза вы­па­ло число, боль­шее 3 равна

Ответ: 0,25.

Ответ: 0,25

0,25

Задание 9 № 325540

31.Стре­лок 4 раза стре­ля­ет по ми­ше­ням. Ве­ро­ят­ность по­па­да­ния в ми­шень при одном вы­стре­ле равна 0,5. Най­ди­те ве­ро­ят­ность того, что стре­лок пер­вые 3 раза попал в ми­ше­ни, а по­след­ний раз про­мах­нул­ся.

Решение.

Вероятность про­ма­ха равна 1 − 0,5 = 0,5. Ве­ро­ят­ность того, что стре­лок пер­вые три раза попал в ми­ше­ни равна 0,5³ = 0,125. Откуда, ве­ро­ят­ность со­бы­тия, при ко­то­ром стре­лок сна­ча­ла три раза по­па­да­ет в мишени, а четвёртый раз про­ма­хи­ва­ет­ся равна 0,125 · 0,5 = 0,0625.

Ответ: 0,0625.

Ответ: 0,0625

0,0625

Задание 9 № 325560

32.В таб­ли­це пред­став­ле­ны ре­зуль­та­ты четырёх стрел­ков, по­ка­зан­ные ими на тре­ни­ров­ке.

Номер стрелка	Число выстрелов	Число попаданий

Тре­нер решил по­слать на со­рев­но­ва­ния того стрел­ка, у ко­то­ро­го от­но­си­тель­ная ча­сто­та по­па­да­ний выше. Кого из стрел­ков вы­бе­рет тре­нер? Ука­жи­те в от­ве­те его номер.

Решение.

Найдём от­но­си­тель­ную ча­сто­ту по­па­да­ний каж­до­го из стрелков:

Заметим, что Приведём и к об­ще­му зна­ме­на­те­лю и сравним: Таким образом, наи­боль­шая от­но­си­тель­ная ча­сто­та по­па­да­ний у четвёртого стрелка.

Ответ: 4.

Ответ: 4

Задание 9 № 325580

33.В ма­га­зи­не канц­то­ва­ров продаётся 100 ручек, из них 37 – крас­ные, 8 – зелёные, 17 – фи­о­ле­то­вые, ещё есть синие и чёрные, их по­ров­ну. Най­ди­те ве­ро­ят­ность того, что Алиса на­у­гад вы­та­щит крас­ную или чёрную ручку.

Решение.

Найдём ко­ли­че­ство чёрных ручек: Ве­ро­ят­ность того, что Алиса вы­та­щит на­у­гад крас­ную или чёрную ручку равна

Ответ: 0,56.

Ответ: 0,56

0,56

Источник: Банк заданий ФИПИ

Задание 9 № 341531

34.В сред­нем из 100 кар­ман­ных фонариков, по­сту­пив­ших в продажу, во­семь неисправных. Най­ди­те ве­ро­ят­ность того, что вы­бран­ный на­уда­чу в ма­га­зи­не фо­на­рик ока­жет­ся исправен.

Расчеты по формулам

Вычисление по формуле

Разные задачи

Линейные уравнения

Вычисление по формуле

Задание 13 № 202

1.В фирме «Эх, прокачу!» сто­и­мость поездки на такси (в рублях) рас­счи­ты­ва­ет­ся по фор­му­ле , где 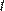— дли­тель­ность поездки, вы­ра­жен­ная в ми­ну­тах . Поль­зу­ясь этой формулой, рас­счи­тай­те стоимость 8-минутной поездки.

Решение.

Подставим в фор­му­лу значение пе­ре­мен­ной :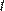

Ответ: 183.

Ответ: 183

Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1303.

Задание 13 № 311326

2.Площадь па­рал­ле­ло­грам­ма можно вы­чис­лить по фор­му­ле , где — сто­ро­ны параллелограмма (в метрах). Поль­зу­ясь этой формулой, най­ди­те площадь параллелограмма, если его сто­ро­ны 10 м и 12 м и .

Решение.

Подставим в фор­му­лу известные зна­че­ния величин:

Ответ: 60.

Ответ: 60

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 1)

Задание 13 № 311533

3.В фирме «Чистая вода» сто­и­мость (в рублях) ко­лод­ца из же­ле­зо­бе­тон­ных колец рас­счи­ты­ва­ет­ся по фор­му­ле , где — число колец, уста­нов­лен­ных при рытье колодца. Поль­зу­ясь этой формулой, рас­счи­тай­те стоимость ко­лод­ца из 11 колец.

Решение.

Подставим ко­ли­че­ство колец в фор­му­лу для рас­че­та стоимости. Имеем:

Ответ: 50 500.

Ответ: 50500

Источник: ГИА-2013. Математика. Экзамен. Вариант 17

Задание 13 № 338071

4.Зная длину сво­е­го шага, че­ло­век может приближённо под­счи­тать пройденное им рас­сто­я­ние s по фор­му­ле s = nl, где n — число шагов, l — длина шага. Какое рас­сто­я­ние прошёл человек, если l = 80 см, n = 1600? Ответ вы­ра­зи­те в километрах.

Решение.

Найдём какое рас­сто­я­ние прошёл человек, под­ста­вим длину шага и число шагов в формулу:

Ответ: 1,28

Ответ: 1,28

1,28

Задание 13 № 338396

5.Расстояние s (в метрах) до места удара мол­нии можно приближённо вы­чис­лить по фор­му­ле s = 330t, где t — ко­ли­че­ство секунд, про­шед­ших между вспыш­кой молнии и уда­ром грома. Определите, на каком рас­сто­я­нии от места удара мол­нии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округ­лив его до целых.

Решение.

Найдем расстояние, на ко­то­ром находится на­блю­да­тель от места удара молнии:

Ответ: 3.

Ответ: 3

Задание 13 № 341532

6.Из фор­му­лы цен­тро­стре­ми­тель­но­го уско­ре­ния a = ω²R най­ди­те R (в метрах), если ω = 4 с⁻¹ и a = 64 м/с².

Линейные уравнения

Задание 13 № 311337

1.Длину окружности можно вы­чис­лить по фор­му­ле , где — ра­ди­ус окружности (в метрах). Поль­зу­ясь этой формулой, най­ди­те радиус окружности, если её длина равна 78 м. (Считать ).

Решение.

Выразим ра­ди­ус из фор­му­лы длины окружности:

Подставляя, получаем:

Ответ: 13.

Ответ: 13

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 2)

Задание 13 № 311348

2.Площадь ромба можно вы­чис­лить по фор­му­ле , где — диа­го­на­ли ромба (в метрах). Поль­зу­ясь этой формулой, най­ди­те диагональ , если диа­го­наль равна 30 м, а пло­щадь ромба 120 м².

Решение.

Подставим в фор­му­лу известные величины:

Ответ: 8.

Ответ: 8

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 3)

Задание 13 № 311528

3.Площадь тре­уголь­ни­ка можно вы­чис­лить по фор­му­ле , где — сто­ро­на треугольника, — высота, про­ве­ден­ная к этой сто­ро­не (в метрах). Поль­зу­ясь этой формулой, най­ди­те сторону , если пло­щадь треугольника равна , а вы­со­та равна 14 м.

Решение.

Выразим сто­ро­ну из фор­му­лы площади треугольника:

Подставляя, получаем:

Ответ: 4.

Ответ: 4

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 4)

Задание 13 № 311530

4.Площадь тра­пе­ции можно вы­чис­лить по фор­му­ле , где — ос­но­ва­ния трапеции, — вы­со­та (в метрах). Поль­зу­ясь этой формулой, най­ди­те высоту , если ос­но­ва­ния трапеции равны и , а её пло­щадь .

Решение.

Выразим вы­со­ту трапеции из фор­му­лы площади:

Подставляя, получаем:

Ответ: 4.

Приведём дру­гое решение.

Подставим в фор­му­лу известные зна­че­ния величин:

Ответ: 4

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.6)

Задание 13 № 311535

5.Радиус впи­сан­ной в пря­мо­уголь­ный тре­уголь­ник окруж­но­сти можно найти по фор­му­ле , где и — катеты, а — ги­по­те­ну­за треугольника. Поль­зу­ясь этой формулой, най­ди­те , если и .

Решение.

Подставим в фор­му­лу из­вест­ные зна­че­ния величин:

Ответ: 3,2.

Ответ: 3,2

3,2

Источник: ГИА-2013. Математика. Московская обл. Пробные варианты(2 вар)

Задание 13 № 311541

6.Объём пи­ра­ми­ды вычисляют по фор­му­ле , где — пло­щадь основания пирамиды, — её высота. Объём пи­ра­ми­ды равен 40, пло­щадь основания 15. Чему равна вы­со­та пирамиды?

Решение.

Выразим вы­со­ту пирамиды из фор­му­лы для ее объема:

Подставляя, получаем:

Ответ: 8.

Ответ: 8

Источник: ГИА-2013. Математика. Тренировочная работа № 3. (1 вар)

Задание 13 № 311543

7.Площадь лю­бо­го вы­пук­ло­го че­ты­рех­уголь­ни­ка можно вы­чис­лять по фор­му­ле , где — длины его диагоналей, а угол между ними. Вы­чис­ли­те , если .

Решение.

Выразим :

Подставляя, получаем:

Ответ: 0,4.

Ответ: 0,4

0,4

Источник: ГИА-2012. Математика. Диагностическая работа № 1(2 вар)

Задание 13 № 311824

8.Чтобы пе­ре­ве­сти зна­че­ние тем­пе­ра­ту­ры по шкале Цель­сия (t °C) в шкалу Фа­рен­гей­та (t °F), поль­зу­ют­ся фор­му­лой F = 1,8C + 32 , где C — гра­ду­сы Це