Числовая последовательность.

Числовая последовательность.

Если всякому натуральному числу (номеру места) по какому-нибудь закону однозначно поставлено в соответствие определенное число (член последовательности), говорят, что задана бесконечная числовая последовательность.

x₁, x₂, x₃, x₄, x₅, x₆,…., x_n – числовая последовательность.

x_n – n-ый член последовательности.

Последовательность – это частный случай функции. Ее областью определения является множество натуральных чисел. Последовательность можно задать формулой.

Пример:

1. x_n =2n – 1. Вычислим x₁ = 2•1 – 1=1, x₂ = 3, x₃ = 5 …. Т.е. последовательность 1, 3, 5, …

2.x_n = 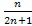Последовательность 1/3, 2/5, 3/7, ….

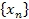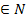Последовательность (n ) называется возрастающей,если для любого натурального n выполняется неравенство 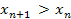. Пример 1.

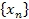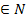Последовательность (n ) называется убывающей,если для любого натурального n выполняется неравенство 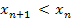. Пример 2.

Возрастающие и убывающие последовательности называются монотонными последовательностями.

Последовательность 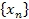называется ограниченной, если существуют два числа m и M такие, что для всех n 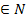выполняется неравенство, .

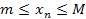Пример: 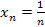- ограниченная 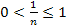, т.к. существуют 2 числа m=0 и M=1.

Предел числовой последовательности.

Пусть номер n неограниченно увеличивается, т.е. стремится к бесконечности ( 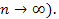При этом соответствующие значения последовательности 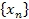приближаются к некоторому числу a. Число a называется пределом последовательности 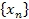и записывается 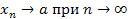или .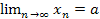

Число a называется пределом последовательности 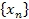, если для любого сколь угодно малого положительного числа 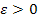найдется такое натуральное число N, что при всех n > N выполняется неравенство 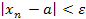, т.е. расстояние от N до a будут меньше .

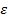Если последовательность 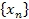имеет конечный предел, то она называется сходящейся.

Пример: предел последовательности 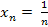стремится к 0, т.е. последовательность сходящаяся.

Если последовательность 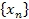предела не имеет (либо предел равен 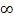), то она называется расходящейся.

Пример: последовательность 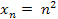не имеет предела, т.е. она расходящаяся.

Бесконечно малые и бесконечно большие величины

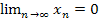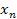Если , то называется бесконечно малой величиной.

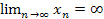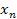Если , то называется бесконечно большой величиной.

Предел функции

Если при 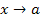функция f(x) стремится к числу А, то число А называется пределом функции в точке а.

Пример: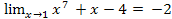

Основные свойства пределов функции

1. Предел алгебраической двух функций, имеющих пределы при 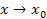равен алгебраической сумме пределов этих функций,

т.е.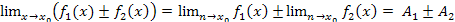

2. Предел произведения двух функций, имеющих пределы при 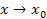равен произведению пределов этих функций,

т.е.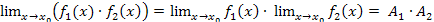

3. Предел частного двух функций, имеющих пределы при 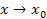равен частного пределов этих функций,

т.е.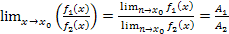

Первый и второй замечательный предел

Первый замечательный предел

Функция 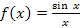в точке x=0определена, тем не менее,

ее предел при 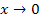существует, причем 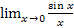= 1

Второй замечательный предел

Выражение 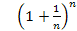, где n - натуральное число, стремится к определенному пределу, когда число 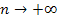. Этот предел больше 2 и меньше 3.

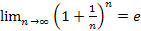
Следствие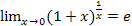

Асимптоты графика функции

Прямая x=x₀ , параллельная оси OY, называется вертикальной асимптотой графика функции y=f(x), если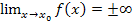

Прямая линия называется наклонной (горизонтальной) асимптотой графика функции y=f(x), если расстояние от произвольной точки М графика до этой прямой стремится к 0 при неограниченном удалении точки от начала координат, т.е. .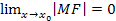

Формула наклонной асимптоты y=kx+b, где k= 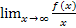, b=

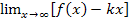
Определенный интеграл

Определенным интегралом от функции y=f(x) на отрезке [a;b] (или в пределах от до) называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к 0: (рисунок)

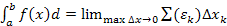
Если f(x)>0 на [a;b], то определенный интеграл геометрически представляет собой площадь криволинейной трапеции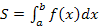

Формула Ньютона-Лейбница

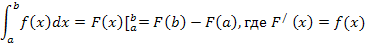
Матрицы. Умножение матриц.

Матрица– это прямоугольная таблица каких-либо элементов a _{i j,}

где i – число строк, j – число столбцов.

У каждого числа свое местоположение, и переставлять их нельзя!

Матрицы обозначают прописными латинскими буквами A, B, C…

Когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Например, матрица размером 2×2, 2×3, 1×4

А= 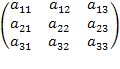- матрица состоит из 9 элементов, 3 строк и 3 столбцов

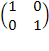– единичная матрица – это матрица, сотоящая из 0 и 1.

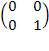нулевая матрица – это матрица, состоящая из 0.

Если в матрице один столбец или одна строка, то такие матрицы называют векторам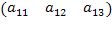и: или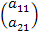

Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной (3×3, 2×2).

Действия с матрицами.

Умножение матриц.

Чтобы матрицу A можно было умножить на матрицу B нужно, чтобы число столбцов матрицыAравнялось числу строк матрицы B.

Пример 1:

A•B = • =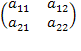

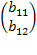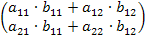
А вот если такие матрицы переставить местами, то, в данном случае, умножение уже невозможно!

Пример 2:

A•B = • =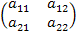

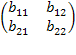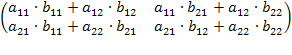
При умножении переставлять матрицы нельзя! Т.е.A•B ≠ B•A

Пример 3:

A•B =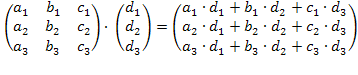

Пример 4:

A•B =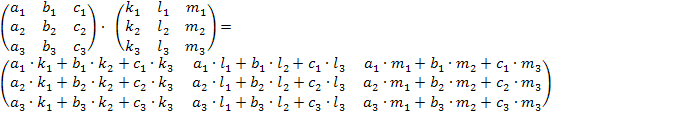

Определитель матрицы

Определитель существует только у квадратных матриц.

Определитель квадратной матрицы 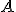будем обозначать 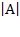или Δ А.

В литературе вместо термина "определитель" используется также термин "детерминант", имеющий тот же самый смысл. От слова "детерминант" и появилось обозначение det .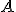
Определение 1. Определителем квадратной матрицы A = 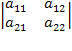второго порядка называется число ΔА= a_11• a₂₂ – a_21• a₁₂

Определение 2. Определителем квадратной матрицы A = 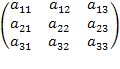третьего порядка называется число ΔА=(a_11• a_22• а₃₃+ a_13• a_21• а₃₂ +a_31• a_12• а₂₃) - (a_13• a_22• а₃₁+ a_11• a_23• а₃₂ +a_21• a_12• а₃₃)

Определение 3. Определителем квадратной матрицы четвертого порядка называется число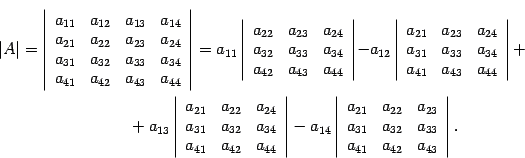

Числовая последовательность.

Если всякому натуральному числу (номеру места) по какому-нибудь закону однозначно поставлено в соответствие определенное число (член последовательности), говорят, что задана бесконечная числовая последовательность.

x₁, x₂, x₃, x₄, x₅, x₆,…., x_n – числовая последовательность.

x_n – n-ый член последовательности.

Последовательность – это частный случай функции. Ее областью определения является множество натуральных чисел. Последовательность можно задать формулой.

Пример:

1. x_n =2n – 1. Вычислим x₁ = 2•1 – 1=1, x₂ = 3, x₃ = 5 …. Т.е. последовательность 1, 3, 5, …

2.x_n = 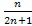Последовательность 1/3, 2/5, 3/7, ….

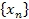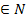Последовательность (n ) называется возрастающей,если для любого натурального n выполняется неравенство 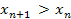. Пример 1.

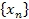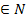Последовательность (n ) называется убывающей,если для любого натурального n выполняется неравенство 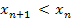. Пример 2.

Возрастающие и убывающие последовательности называются монотонными последовательностями.

Последовательность 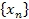называется ограниченной, если существуют два числа m и M такие, что для всех n 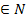выполняется неравенство, .

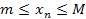Пример: 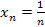- ограниченная 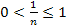, т.к. существуют 2 числа m=0 и M=1.

Предел числовой последовательности.

Пусть номер n неограниченно увеличивается, т.е. стремится к бесконечности ( 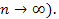При этом соответствующие значения последовательности 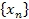приближаются к некоторому числу a. Число a называется пределом последовательности 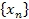и записывается 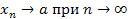или .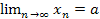

Число a называется пределом последовательности 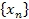, если для любого сколь угодно малого положительного числа 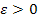найдется такое натуральное число N, что при всех n > N выполняется неравенство 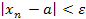, т.е. расстояние от N до a будут меньше .

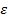Если последовательность 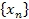имеет конечный предел, то она называется сходящейся.

Пример: предел последовательности 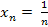стремится к 0, т.е. последовательность сходящаяся.

Если последовательность 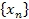предела не имеет (либо предел равен 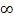), то она называется расходящейся.

Пример: последовательность 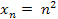не имеет предела, т.е. она расходящаяся.