Лабораторная работа 6. кластерный анализ

Цель: углубление знаний по методам классификации и сокращения размерности признакового пространства, привитие навыков визуальной классификации в пространстве малой размерности.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Основные положения кластерного анализа

Кластерный анализ ставит своей задачей разбиение множества из N объектов {X₁,X₂,…,X_N}, для каждой пары которых заданы значения некоторой меры близости (сходства) или различия (расстояния), на k<N подмножеств (кластеров) так, чтобы каждый объект принадлежал одному и тому же кластеру, должны быть сходными (близкими), тогда как объекты из разных кластеров должны быть несходными (далекими).

Значение меры близости s или различия d либо заданы заранее, либо вычисляются как некоторая свертка значений одноименных признаков объектов. В качестве такой свертки широко применяют евклидово расстояние. Использование обычного евклидова расстояния можно признать оправданным, если:

• отдельные признаки взаимно независимы и имеют одну и ту же дисперсию;
• отдельные признаки однородны по физическому смыслу и одинаково важны с точки зрения задачи классификации;
• пространство признаков совпадает с геометрическим пространством размерности не выше трех.

Наряду с мерами близости d(X_i,X_j) между отдельными объектами процедуры кластерного анализа требуют введения мер близости между группами (кластерами) объектов. Наиболее употребительные расстояния между кластерами K_l , K_m:

1)

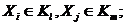расстояние, измеряемое по принципу «дальнего соседа» («nearest neighbour»):

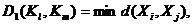2) расстояние, измеряемое по принципу «дальнего соседа» («furthest neighbour»):

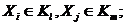3) расстояние, измеряемое по «центру тяжести» кластеров («centroid»):

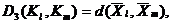где `X<sub>l</sub> ,`X_m – арифметические средние наблюдений, входящих в кластеры K_l, K_m соответственно;

4) расстояние, измеряемое по принципу «средней связи» («average»):

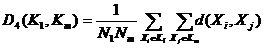Пусть исходное множество О объектов разбито на m подмножеств (групп). Воспользуемся следующими тремя характеристиками степени рассеяния объектов из О:

· общее рассеяние ;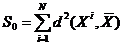

· межгрупповой разброс ;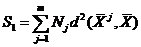

· внутригрупповой разброс ,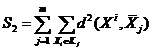

где 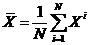– среднее всего множества объектов, иначе общий центр тяжести, 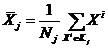– центр тяжести j-й группы, N_j – число объектов в группе К_j.

Можно показать, что для евклидова расстояния общий разброс распадается на межгрупповое и внутригрупповое рассеяния, т.е.

S₀ = S₁ + S₂

Доля межгруппового разброса в общем рассеянии S₁/S₀ показывает долю общего разброса, объясненного классификацией. Легко видеть, что T = 1 – S₂/S₀. Из последней формулы следует, что чем компактнее группы, тем ближе Т к единице, и соответственно лучше качество разбиения. Очевидно, 0 £ Т £ 1.

Разбиение исходной совокупности объектов на кластеры может осуществляться различными способами. Естественно поэтому определить тот количественный критерий, следуя которому можно было бы предпочесть одно разбиение другому. Функционал качества разбиения должен отражать разнородность множества объектов. Широкое распространение для фиксированного разбиения на k классов получил критерий, представляющих собой сумму внутрикластерных «дисперсий»:

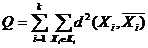Из многообразия способов разбиения исходного множества на известное заранее число объектов упомянем метод К-средних. В этом методе начинают со случайного отбора k объектов, которые принимают за центры кластеров. Затем очередной объект из входного потока данных относят к тому кластеру, до центра которого он наиболее близок. Получившийся кластер из двух объектов заменяют на новый центр, координаты которого вычисляют как среднее координат этих двух объектов. Описанную процедуру повторяют с остальными объектами. При достаточно большом числе классифицируемых объектов имеет место сходимость вектора координат центров кластеризации к некоторому пределу.

Указанные методы предполагают, что число кластеров известно заранее. Для того чтобы оценить ожидаемое число кластеров, прибегают к визуальному представлению исходных объектов на плоскости.

Одной из форм такого представления являются так называемые «звездные диаграммы», число лучей у которых равняется размерности пространства признаков исходных объектов. На этих лучах откладываются отрезки, длина которых пропорциональна значению соответствующего признака. При визуализации с помощью лиц Чернова за каждую часть лица (нос, форма рта, ширина головы, и т.п.) отвечает некая переменная. Таким образом, некую группу похожих лиц можно, выделить в один кластер.

Наряду с обычным, «раздельным», кластерным анализом широко применяется иерархический кластерный анализ, цель которого состоит в получении всей иерархии разбиений, а не отдельного разбиения. Считается, что иерархия точнее характеризует размытую структуру данных, чем отдельное разбиение. Получить конкретное разбиение в случае необходимости сравнительно легко сечением графа иерархий (дендрограммы), что является достоинством иерархического кластерного анализа.

К достоинствам иерархических процедур относят полноту анализа структуры исследуемого множества наблюдений, возможность наглядной интерпретации проведенного анализа, возможности останова процедуры достижении априори заданного числа кластеров. К существенным недостаткам иерархических процедур следует отнести финальную неоптимальность. Как правило, даже подчиняя каждый шаг работы процедуры некоторому критерию качества разбиения, получающееся в итоге разбиение для любого наперед заданного числа кластеров оказывается весьма далеким в смысле того же самого критерия качества.

Задание

1. Получить от преподавателя вариант исходных данных;

2. Провести предварительную визуальную кластеризацию объектов с помощью:

· звездных диаграмм;

· лиц Чернова.

3. С помощью процедуры кластерного анализа провести кластеризацию всеми имеющимися методами (раздельными и иерархическими), задав число кластеров по результатам п.2. задания;

4. Для метода К-средних подсчитать значение критерия качества разбиения.

5. Отчет должен содержать: таблицу исходных данных, «звездные диаграммы» объектов и лица Чернова, принадлежащих кластерам из п.4; значения критерия качества разбиения, анализ результатов кластеризации по стандартизованным данным, содержательную интерпретацию качественной переменной, описывающей результаты кластерного анализа из п.4. задания, а также дендрограмму.

Анализ качества разбиения

Доля межгруппового разброса в общем рассеянии S₁/S₀ показывает долю общего разброса, объясненного классификацией. Критерий качества разбиения T = 1 – S₂/S₀. Из последней формулы следует, что чем компактнее группы, тем ближе Т к единице, и, соответственно, лучше качество разбиения.

0 £ Т £ 1.

Интерпретация результатов

Интерпретация полученных групп базируется на тщательном анализе состава объектов, попавших в одну группу. Определенную помощь здесь может оказать анализ статистических характеристик переменных, описывающих объекты. В частности, переменные, имеющие наименьший разброс, т.е. наименее изменчивые в пределах группы, могут выступать в качестве индикатора, полезного при интерпретации группы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем заключается задача кластерного анализа?
2. Почему задачу кластерного анализа можно отнести к задаче конструирования анализа данных?
3. Чем объясняется широкое применение евклидова расстояния в качестве меры различия?
4. Как соотносятся расстояния, измеренные по принципу “ближайшего соседа”,

“дальнего соседа” и измеряемые по центрам тяжести кластеров?

5.С какой целью вводят функционал качества разбиения на кластеры?

6.В чем сходство и различие методов средних и “зерен”?

7.Что такое “звездная” диаграмма?

8.Какая мера сходства (расстояния) подразумевается при визуальной кластеризации с помощью “звездных диаграмм”?

9.Могут ли пересекаться проекции на плоскости двух выпуклых, разнесенных в пространстве, кластеров?

ЗАДАНИЕ

1.Получить от преподавателя вариант исходных данных.

2.Провести предварительную визуальную кластеризацию объектов с помощью:

а) ”звездных диаграмм”;

б) лиц Чернова;

в) по методу главных компонент.

3.С помощью процедуры кластерного анализа провести кластеризацию всеми имеющимися методами, задав число кластеров по результатам п.2.

4. Подсчитать значение критерия качества разбиения Q .

5. Повторить пп.2-4 для стандартизованных переменных.

6. Отчет должен содержать: таблицу исходных данных, “звездные диаграммы” объектов, принадлежащих кластерам из п.4; значения критерия качества разбиения; сравнительный анализ результатов кластеризации по исходным и стандартизованным данным; интерпретацию качественной переменной, описывающей результаты кластерного анализа из п.4.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА [1,12]