Лабораторная работа 3. сглаживание временного ряда

Цель: практическое освоение методов выделения трендовой составляющей временного ряда простой структуры.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Методы сглаживания временных рядов.

Пусть временной ряд y_t, t = 1,2,…,T может быть представлен в виде аддитивной совокупности двух составляющих: систематической f_t и возмущающей u_t, то есть

y_t = ƒ_t + u_t , t = 1,2,…,T.

Переменная u_t случайна, имеет нулевое математическое ожидание и одинаковую дисперсию при любом t, ее последовательные значения некоррелированы. Величину f_t называют уровнем ряда в момент t, а закон изменения уровня – трендом.

Составляющие f_t и u_t не наблюдаемы. Процесс построения модели, аппроксимирующий тренд, называют сглаживанием временного ряда.

Для выделения тренда используют ряд методов. Метод скользящего среднего (МСС) и метод экспоненциального сглаживания (МЭС) относятся к классу адаптивных, когда параметры модели меняются при переходе от одного наблюдаемого значения к другому. В неадаптивных методах с помощью обычной или взвешенной регрессии строится единая модель для всех наблюдения ряда.

В МСС с помощью метода наименьших квадратов строят полином невысокого порядка для отрезка ряда , содержащего нечетное число точек. В качестве уровня ряда берут значение оцененного полинома в середине отрезка усреднения. Затем переходят к следующему отрезку той же длины, смещенному вправо на один временной такт, и процедуру повторяют.

Ниже приводятся формулы для оценки уровня ряда f_t при длине отрезка 5 временных тактов:

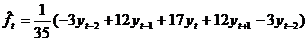и 7 временных тактов:

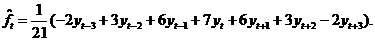Варьируя длину отрезка усреднения, останавливаются на такой, при которой сглаженный ряд почти не содержит краткосрочных колебаний.

В МЭС предполагают, что ряд имеет бесконечную предысторию и с помощью взвешенного метода наименьших квадратов находят коэффициенты полинома P_t от времени t выбранной степени d (как правило, не выше третьей), то есть минимизируют

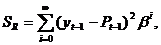Коэффициенты полинома могут быть выражены как линейные комбинации экспоненциальных средних соответствующих порядков. Экспоненциальная средняя первого порядка, иначе модель простого экспоненциального сглаживания, определяемая для полинома нулевой степени (то есть P_t = a_t), имеет вид:

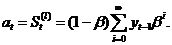Значения коэффициентов полинома в момент t могут быть выражены также через их значения в предыдущие моменты. В качестве примеров приводятся формулы для коэффициентов линейной модели y_{t =}a_t + b_tt + u_t (двойное экспоненциальное сглаживание):

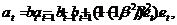Здесь e_t – ошибка прогнозирования на один шаг вперед, то есть e_t=y_t-(a_t-1 + b_t-1l).

Подбирают постоянную сглаживания α = 1 – β эмпирически, исходя из минимума ошибки прогнозирования по оцененной модели.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какой вид имеет корреляционная матрица возмущений u_t (t=1,2,…,T)?
2. Поясните смысл термина “скользящее среднее”.
3. Для сглаживания временного ряда, содержащего лишь случайный компонент u_t, применили МСС с периодом усреднения, равным 5, а затем 7 тактам. В каком случае будет меньше дисперсия сглаженного ряда? Насколько?
4. Для сглаживания ряда п.2 применим простое арифметическое усреднение 7. Будет ли меньшей дисперсия сглаженного ряда по сравнению с МСС с тем же периодом усреднения?
5. В чем отличие адаптивных методов сглаживания от неадаптивных?
6. Как линеаризовать модель ряда, если известно, что возмущения наложены на систематическую составляющую мультипликативно?
7. Из каких соображений выбирают длину отрезка усреднения?
8. Поясните происхождение термина “экспоненциальное сглаживание”.
9. Как определяются экспоненциальные средние высоких порядков?
10. Как ведет себя экспоненциальная средняя первого порядка в сравнении с исходным рядом при α = 1 – β , близком нулю, и α, близком единице?

ЗАДАНИЕ

1. Исследовать реакцию простой модели экспоненциального сглаживания на стандартные входные ряды: одиночный импульс, ступенчатое воздействие, гармонические колебания, воздействие в виде линейной и параболической функций. Каждый ряд должен содержать не менее восьми значений, горизонт предсказаний – не более половины длины ряда. Импульс и ступенька должны появиться за два такта до окончания ряда. Постоянную сглаживания alpha для каждой модели взять равной 0,1 и 0,9.

2.Для задачи прогнозирования на два такта вперед подобрать подходящую модель экспоненциального сглаживания для реального ряда, задаваемого преподавателем.

Подбор проводить по минимуму суммы квадратов отклонений.

3.Для ряда п.2 подобрать неадаптивную модель из числа возможных.

4.Перейти в режим сглаживания и с помощью простого скользящего среднего выделить трендовую составляющую, меняя длину отрезка усреднения.

Требования к отчету

Отчет должен содержать:

- графики исходных стандартных и сглаженных рядов и рекомендации по выбору порядка модели и постоянной сглаживания,

- графики исходного и сглаженного рядов для реальных данных с обоснованием длины отрезка усреднения.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА [9, 12]

Лабораторная работа 4. АНАЛИЗ ВРЕМЕННОГО РЯДА
ПО МЕТОДУ БОКСА-ДЖЕНКИНСА

(интегрированная модель авторегрессии – скользящего среднего)

Цель: привитие умения и навыков построения интегрированной модели авторегрессии – скользящего среднего временного ряда общего вида.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Основные положения метода Бокса-Дженкинса

Рассматривается временной ряд общего вида, содержащий в качестве компонент полиномиальную трендовую составляющую, сезонный эффект, авторегрессионный процесс, в котором допускается коррелированность остатков, и эти корреляции генерированы скользящим средним случайных возмущений.

В методе Бокса-Дженкинса проблема исключения тренда решается путем перехода к разностям ряда подходящего порядка, обеспечивающего их стационарность. Если ввести оператор сдвига назад В, определяемый соотношением By_t=y_t-1, то разность назад первого порядка запишется так:

y_t – y_t-1 = y_t – By_t = (1 –B)y_t,,

а разность порядка d – как (1 – B)^dy_t.

С учетом введенных обозначений модель ряда с мультипликативным сезонным эффектом записывают в следующем виде:

a(B)*a_c (B)*(1-B)^d*(1-B_c)D*y_t = b(B)*b_c(B)*u_t.

Здесь a(B) = (1 - a_1­B - a₂B² -…- a_pB^p) – авторегрессионный оператор порядка р (сокращенно AP(p)) для трендовой составляющей ряда;

a_c(B) = (1 - a₁B - a₂B² -…- a_PB^P) – авторегрессионный оператор порядка P (сокращенно AP(P)) для сезонной составляющей ряда;

(1-B)^d – разность (с лагом 1) порядка d;

1-B_c – первые разности членов с лагами, равными величине периода сезонности (12 – для месячных данных, 4 – для квартальных и т.п., то есть это разности данных за одноименные месяцы, кварталы и т.п.);

b(B) = 1 - b_1­B - b₂B² -…- b_qB^q - оператор процесса скользящего среднего порядка q (сокращенно CC(q)) для трендовой составляющей ряда;

b(B) = 1 - b_1­B - b₂B² -…- b_QB^Q – оператор процесса скользящего среднего порядка Q (сокращенно CC(q)) для сезонной составляющей ряда;

u_t – случайные возмущения с нулевым математическим ожиданием, постоянной дисперсией и некоррелированными значениями для любых t₁ и t₂ (t₁ ≠ t₂).

Работа с моделью проходит как итеративный трехстадийный процесс, включающий идентификацию, оценку параметров и диагностическую проверку модели.

Под идентификацией понимается использование наблюденных данных и любой другой информации для определения возможных значений параметров p,d,q.

Под оценкой понимается эффективное использование данных для получения численных значений параметров модели (5.1) при предположении ее адекватности процессу.

Диагностическая проверка имеет целью проверку адекватности подобранной модели и ее улучшение.

Процесс идентификации начинают с определения порядка разности d, добиваясь того, чтобы ряд разностей был стационарным. Идентификатором стационарности служит поведение корреляционной функции: для стационарного ряда корреляционная функция должна быстро спадать по экспоненте либо по синусоиде, наложенной на экспоненту. Наличие горизонтальных либо слабо падающих участков говорит о том, что ряд нестационарный, но возможно его разность стационарна. Заметим, что на практике d ≤ 2.

Определив экспериментально d, приступают к выбору p и q для процессов авторегрессии и скользящего среднего по автокорреляционной (АФ) и частной автокорреляционной функциям (ЧАФ) разностей порядка d . ЧАФ измеряет корреляцию членов ряда, разнесенных на k тактов, но при условии, что взаимозависимость между промежуточными членами ряда, отстоящими друг от друга меньше, чем на k, устранена, иначе элиминирована .

Для большинства практических задач p,d,q не превышает двух. Закономерности, имеющие место для моделей невысокого порядка, приведены в таблице.

Модель	Поведение АФ(k)	Поведение ЧАФ(k)
(1, d, 0)	Убывает экспоненциально	Не равна нулю только при k=1
(0, d, 1)	Не равна нулю только при k=1	Доминирует экспоненци- альное затухание
(2, d, 0)	Наложение затухающих экспонент и синусоид	Не равна нулю только при k=1 и k=2
(0, d, 2)	Не равна нулю только при k=1 и k=2	Доминирует наложение затухающих экспонент и синусоид
(1, d, 1)	Экспоненциально убывает, начиная с k=1	Начиная с k=1, доминирует затухающая экспонента

Заметим, что конечность выборки, по которой строится АФ и ЧАФ, вносят искажения в поведение функций, что приводит к затруднениям при выборе p,d,q. Поэтому для анализа берут несколько моделей.

Проверка адекватности модели основана на анализе автокорреляционной функции остатков. Если модель адекватна исследуемому процессу, то остатки, равные разности между наблюдаемыми значениями ряда и оценками, полученными по модели, будут некоррелированы, а значения автокорреляции распределены приблизительно нормально около нуля с дисперсией, равной 1/(N-d), где N – число наблюдений в выборке.

Помимо анализа отдельных коэффициентов автокорреляции остатков возможен общий совокупный тест автокорреляционной функции остатков. Пусть имеется K оценок автокорреляций r_u(k), k = 1,2,…,K. В случае адекватности построенной модели временному ряду, случайная величина

h = ( N-d )( r_u²(1) + r_u²(2) + … + r_u²(K))

распределена по закону xи-квадрат с (K-p-q) степенями свободы. При неадекватности модели автокорреляции остатков будут существенными, а величина h большой.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Какие компоненты входят в модель АРИСС?

2.Запишите в явном виде, без использования оператора сдвига, модель (5.1) в случае отсутствия сезонного эффекта:

а) для авторегрессионного процесса порядка два;

б)для процесса скользящего среднего первого порядка;

в)для смешанного процесса АРСС с p=1 и q=2.

3.Почему работа с моделью АРИСС носит итеративный характер?

4.Что понимают под идентификацией модели АРИСС?

5.Что такое частная автокорреляционная функция?

6.Как соотносятся поведение АФ и ЧАФ в моделях (1,d,0) и (0,d,1)?

7.Каковы признаки стационарности временного ряда?

8.Для какого процесса автокорреляционная функция представляет собой наложение затухающих экспонент и синусоид?

9.Каким предпосылкам удовлетворяют случайные возмущения в модели АРИСС?

10.Как вычисляются разности порядка выше первого?

11.Как воспользоваться статистикой h?

ЗАДАНИЕ

1.Получить от преподавателя вариант исходных данных.

2.Перейти в режим горизонтального графика временного ряда (Horisontal Time Sequence Plot) раздела Time Series Analysis.

3.Провести визуальный анализ ряда, получить ответы на вопросы:

а)стационарный ли ряд?

б)существует ли тренд?

в)какого порядка полином?

г)есть ли сезонный эффект?

д)какова длина сезонного эффекта?

4.Перейти в режим анализа временных рядов методом Бокса-Дженкинса (Box-Jenkis ARIMA Modeling) раздела Time Series Analysis.

5.Указать исследуемый ряд, отбросив 4 последние наблюдения (оператор DROP).

6.Подобрать параметры p,d,q для несезонной и P,D,Q для сезонной составляющих модели ARIMA, начав с нулевых значений и используя принцип максимальной простоты модели. При идентификации модели и для оценки результатов моделирования использовать функции автокорреляции (ACF) и частной корреляции (PACF).

7.После построения модели использовать ее для прогноза четырех точек. Построить график предсказанных значений. Результаты предсказаний сохранить в рабочей переменной Work Area-Forecasts и сравнить с реальными данными. В случае выхода за границы доверительных интервалов повторить построение модели.

8.Отчет должен содержать описание исходных данных, график временного ряда, результаты визуального анализа, график функций ACF и PACF для начальных и конечных значений параметров p,d,q,P,D,Q, аналитический вид полученной модели, результаты предсказаний, реальные данные и доверительные интервалы, результаты тестирования автокорреляционной функции остатков для окончательной модели.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА [6,9, 12, 13, 15цй]