Условное математическое ожидание
Определение 1. Условным математическим ожиданием непрерывной СВ X при условии, что непрерывная СВ Y приняла значение y, называется в случае абсолютной сходимости интеграла, функция y:
| M[X|y] | Δ = | +∞ ∫ -∞ | xfX(x|y) dx . |
Замечание 1. В случае дискретных СВ X и Y условное МО СВ X при условии, что Y = yj, j = 0,m, определяется формулой
| M[X|yj] | Δ = | n ∑ i=0 | xi | pij pj | , j = 0,m, |
где
| pij | Δ = | P{X = xi, Y = yj} , pj | Δ = | P{Y = yj}. |
Определение 2. Условное математическое ожидание M[X|y] СВ X как функция параметра y R1 называется регрессией X на y. График функции x = M[X|y] называется кривой регрессии X на y. Аналогично определяется условное МО СВ
при условии, что Y = y. Например, для непрерывных X и Y:
| M[φ(x)|y] | Δ = | +∞ ∫ -∞ | φ(x)fX(x|y) dx . |
| M[φ(Y)X|y] | = | +∞ ∫ -∞ | φ(y)xfX(x|y) dx = φ(y)M[X|y]. |
| Z | Δ = | φ(x) |
| M[X|y] | Δ = | +∞ ∫ -∞ | xfX(x|y) dx | 5)f(x|y) = | +∞ ∫ -∞ | xf(x) dx | Δ = | M[X]. |
С в о й с т в а M[X | y] : 1) M[φ(Y)|y] = φ(y), где φ(y) -- некоторая функция.2) M[φ(Y)X|y] = φ(y)M[X|y]. Действительно, например, в случае непрерывных СВ X и Y имеем 3) M[X + φ(Y)|y] = M[X|y] + φ(y). Это свойство доказывается аналогично свойству 2)M[X|y]. 4) M[X|y] = M[X], если X и Y -- независимы. Пусть, например, СВ X и Y -- непрерывны, тогда
5) M[X] = M[M[X|Y]], т.е. справедлива формула полного математического ожидания. Пусть СВ X и Y непрерывны, тогда
| M[X] | Δ = | +∞ ∫ -∞ | xfX(x) dx | 6)f(x,y) = | +∞ ∫ -∞ | x( | +∞ ∫ -∞ | f(x,y) dy) dx | Л8.Р2.З2 = |
| = | +∞ ∫ -∞ | x( | +∞ ∫ -∞ | fY(y)fX(x|y) dy) dx = | +∞ ∫ -∞ | fY(y)( | +∞ ∫ -∞ | xfX(x|y) dx) dy = |
Ковариация
| = | +∞ ∫ -∞ | fY(y)M[X|y] dy = M[M[X|Y]]. |
Если между случайными величинами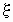 
и 
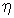существует стохастическая связь, то одним из параметров, характеризующих меру этой связи является ковариация 
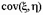. Ковариацию вычисляют по формулам
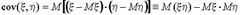
Если случайные величины 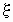и 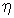независимы, то 
.
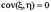Обратное, вообще говоря, неверно. Из равенства нулю ковариации не следует независимость случайных величин. Случайные величины могут быть зависимыми в то время как их ковариация — нулевая!
Но зато, если ковариация случайных величин отлична от нуля, то между ними существует стохастическая связь, мерой которой и является величина ковариации.
Интересно отметить, что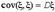 
и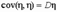 
.
Кроме того, важны следующие свойства ковариации:
;
;
.
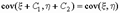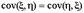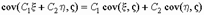Корреляция
Понятно, что значение ковариации зависит не только от “тесноты” связи случайных величин, но и от самих значений этих величин, например, от единиц измерения этих значений.
Для исключения этой зависимости вместо ковариации используется коэффициент корреляции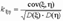 
.
Этот коэффициент обладает следующими свойствами:
он безразмерен;его модуль не превосходит единицы, т.е.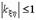 
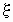;если и 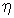независимы, то 
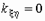(обратное, вообще говоря неверно!);
если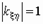 
, то случайные величины 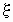и 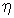связаны функциональной зависимостью вида 
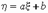, где 
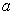и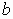 
— некоторые числовые коэффициенты;
;
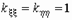Корреляционным моментом СВ x и h называется мат. ожидание произведения отклонений этих СВ. mxh=М((x—М(x))*(h—М(h)))
Для вычисления корреляционного момента может быть использована формула:
mxh=М(x*h)—М(x)*М(h) Доказательство: По определению mxh=М((x—М(x))*(h—М(h))) По свойству мат. ожидания
mxh=М(xh—М(h)—hМ(x)+М(x)*М(h))=М(xh)—М(h)*М(x)—М(x)*М(h)+М(x)*М(h)=М(xh)—М(x)*(h)
Предполагая, что x и h независимые СВ, тогда mxh=М(xh)—М(x)*М(h)=М(x)*М(h)—М(x)*М(h)=0; mxh=0. Можно доказать, что если корреляционный момент=0, то СВ могут быть как зависимыми, так и независимыми. Если mxh не равен 0, то СВ x и h зависимы. Если СВ x и h зависимы, то корреляционный момент может быть равным 0 и не равным 0. Можно показать, что корреляционный момент характеризует степень линейной зависимости между составляющими x и h. При этом корреляционный момент зависит от размерности самих СВ. Чтобы сделать характеристику линейной связи x и h независимой от размерностей СВ x и h, вводится коэффициент корреляции:
Кxh=mxh/s(x)*s(h) Коэффициент корреляции не зависит от разностей СВ x и h и только показывает степень линейной зависимости между x и h, обусловленную только вероятностными свойствами x и h. Коэффициент корреляции определяет наклон прямой на графике в системе координат (x,h) Свойства коэффициента корреляции.
1. -1<=Кxh<=1
Если Кxh =±1, то линейная зависимость между x и h и они не СВ.
2. Кxh>0, то с ростом одной составляющей, вторая также в среднем растет.
Кxh<0, то с убыванием одной составляющей, вторая в среднем убывает.
3. D(x±h)=D(x)+D(h)±2mxh
Доказательство.
D(x±h)=M((x±h)2)—M2(x±h)=M(x2±2xh+h2)—(M(x)±M(h))2=M(x2)±2M(xh)+M(h2)—+M2(x)+2M(x)*M(h)—M2(h)=D(x)+D(h)±2(M(xh))—M(x)*M(h)=D(x)+D(h)±2mxh