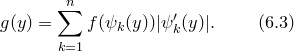Функции случайных величин. Вычисление математических ожиданий. Нахождение закона распределения для функции одной случайной величины в случае дискретной и непрерывной случайной величины.

Пусть случайная величинаY является функцией случайного аргумента X с заданным законом распределения

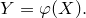
Требуется, не находя закона распределения величины Y, определить ее математическое ожидание

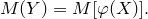
ПустьX — дискретная случайная величина, имеющая ряд распределения

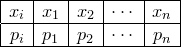
Составим таблицу значений величины Y и вероятностей этих значений:

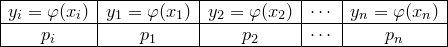
Эта таблица не является рядом распределения случайной величины Y, так как в общем случае некоторые из значений могут совпадать между собой и значения в верхней строке не обязательно идут в возрастающем порядке. Однако математическое ожидание случайной величины Y можно определить по формуле

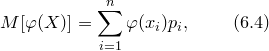
Для непрерывной случайной величины математическое ожидание вычисляется по формуле

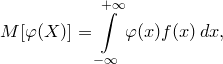
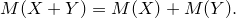где f(x) — плотность распределения вероятностей случайной величины X.

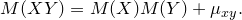1.

2.

µ_xy- корреляционный момент

Следствие.1. Математическое ожидание произведения двух некоррелированных случайных величин равно произведению их математических ожиданий.

Следствие 2. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

Дана система случайных величин 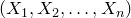, закон распределения которой известен. Рассматривается некоторая случайная величина Y как функция данных случайных величин:

Требуется определить закон распределения случайной величины Y, зная вид функций (6.1) и закон совместного распределения ее аргументов.

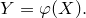
Пусть X — дискретная случайная величина, имеющая ряд распределения

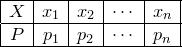
Тогда Y также дискретная случайная величина с возможными значениями 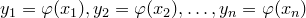. Если все значения 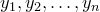различны, то для каждого 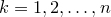события 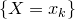и 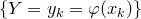тождественны. Следовательно,

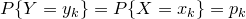
и искомый ряд распределения имеет вид

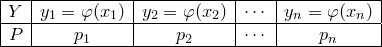
Если же среди чисел 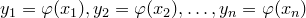есть одинаковые, то каждой группе одинаковых значений 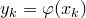нужно отвести в таблице один столбец и соответствующие вероятности сложить.

Для непрерывных случайных величин задача ставится так: зная плотность распределения 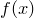случайной величины 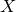, найти плотность распределения 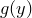случайной величины 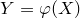. При решении поставленной задачи рассмотрим два случая.

Предположим сначала, что функция 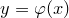является монотонно возрастающей, непрерывной и дифференцируемой на интервале 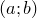, на котором лежат все возможные значения величины X. Тогда обратная функция 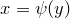существует, при этом являясь также монотонно возрастающей, непрерывной и дифференцируемой. В этом случае получаем

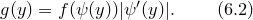
Рассмотрим случай немонотонной функции. Пусть функция 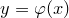такова, что обратная функция 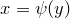неоднозначна, т. е. одному значению величины y соответствует несколько значений аргумента x , которые обозначим 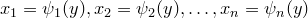, где n — число участков, на которых функция 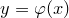изменяется монотонно. Тогда