Скорости и ускорения точек вращающегося твердого тела

Так как траектории точек вращающегося тела – окружности, при определении скорости и ускоренияудобно воспользоваться естественным способом задания движения (рисунок 1.5).

Дуговая координата, определяющая положение точки на траектории, связана с углом поворота равенством:

s = φR

Отсюда:

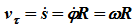
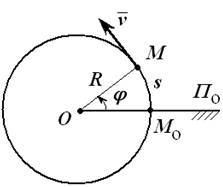
Рис. 1.5

Скорость ν = ν_ττ еще называют линейной или окружной скоростью. Она направлена по касательной к траектории движения точки.

Ускорение (рисунок 1.6) определяется как сумма касательного и нормального ускорений:

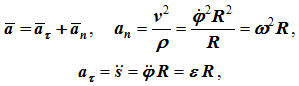
модуль ускорения

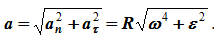
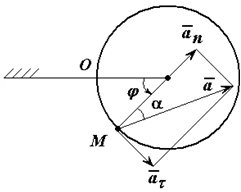
Рис. 1.6

Угол α, образованный вектором ускорения точки с радиусом окружности OM, для всех точек тела в любой момент времени одинаков,

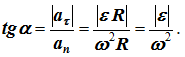
Касательное и нормальное ускорения при вращательном движении твердого тела также называют соответственно вращательным и центростремительным:

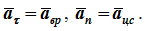
Векторные выражения скорости и ускорения точек вращающегося тела

Модуль скорости точки вращающегося тела (рис. 1.7)

ν = ωR = ωrsinβ

равен модулю векторного произведения ω × r.

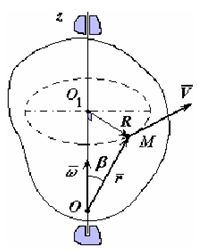
Рис. 1.7

Следовательно:

ν = ω × r (формула Эйлера).

Определим ускорение точки, продифференцировав формулу Эйлера:

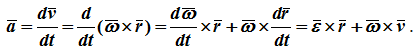
Первое слагаемое является касательным ускорением

a_τ= ε × r,

а второе – нормальным

a_n = ω × (ω × r) = ω × ν.

Плоскопараллельное (плоское) движение твердого гола. Уравнения движения плоской фигуры. Скорости точек плоской фигуру. Мгновенный центр скоростей. Ускорения точек плоской фигуры. Мгновенный центр ускорений. Формулы для нахождения угловой скорости и углового ускорения фигуры.

Плоское движение твердого тела

Определение

Плоским движением твердого тела называется такое его движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости (рис. 1.1).

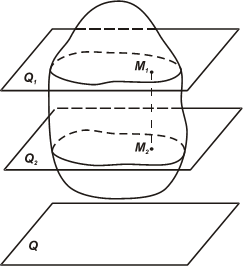
Рис. 1.1

То есть точки М₁ и М₂ тела А, например, двигаются в плоскостях Q₁ и Q₂, соответственно параллельных плоскости Q.

Закон движения

Если в первоначальной момент отрезок М₁М₂перпендикулярен плоскостям Q, Q₁, Q₂, то и при последующем движении тела он остается параллельным своему первоначальному положению и перпендикулярным к этим плоскостям, т.е. движется поступательно. Следовательно, скорости и ускорения всех точек тела, лежащих на отрезке М₁М₂, равны и одинаково направлены.

Это позволяет свести изучение движение отрезка М₁М₂к изучению движения точки М₁ или М₂ вместе с соответствующим сечением тела в плоскости (рис. 1.2).

Положение фигуры в плоскости вполне определяется положением в этой плоскости какого-нибудь отрезка, например АВ, скрепленного с фигурой. Положение отрезка будет вполне определено, если будет известно положение какой-либо точки, например А (полюс), и угла наклона (φ) отрезка к выбранной оси.

Тогда закон движения фигуры в плоскости может быть записан в виде

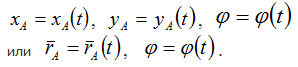
В учебной литературе показано, что закон вращательного движения не зависит от выбора полюса.

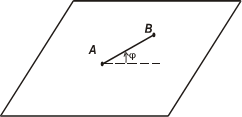
Рис. 1.2