Центр тяжести твердого тела. Способы нахождения центра тяжести.

Центр тяжести твердого тела

Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела (рисунок 1.6).

Радиус-вектор этой точки

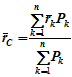
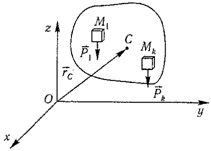
Рисунок 1.6

Для однородного тела положение центра тяжести тела не зависит от материала, а определяется геометрической формой тела.

Если удельный вес однородного тела γ, вес элементарной частицы тела

P_k= γΔV_k (P = γV)

подставить в формулу для определения r_C, имеем

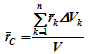
Откуда, проецируя на оси и переходя к пределу, получаем координаты центра тяжести однородного объема

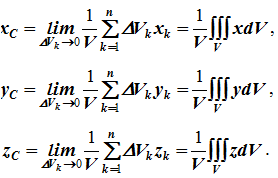
Аналогично для координат центра тяжести однородной поверхности площадью S (рисунок 1.7, а)

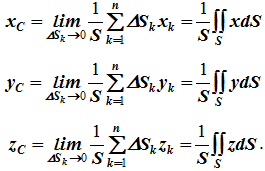
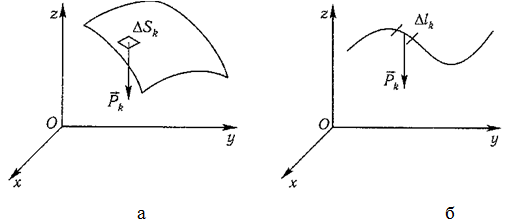
Рисунок 1.7

Для координат центра тяжести однородной линии длиной L (рисунок 1.7, б)

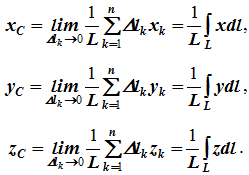
Способы определения координат центра тяжести

Исходя из полученных ранее общих формул, можно указать способы определения координат центров тяжести твердых тел:

• 1 Аналитический (путем интегрирования).
• 2 Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжестилежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
• 3 Экспериментальный. (метод подвешивания тела).
  Этот способ подходит в основном для плоских и линейных тел.
• 4 Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S₁ и S₂ (S = S₁+ S₂). Центры тяжести этих фигур находятся в точках C₁(x₁, y₁) и C₂(x₂, y₂). Тогда координаты центра тяжести тела равны:
  
  

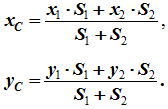
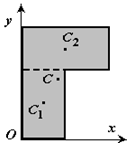
Рисунок 1.8

• 5 Дополнение (Метод отрицательных площадей или объемов).
  Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
  
  

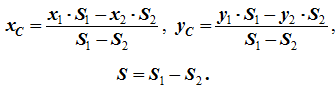
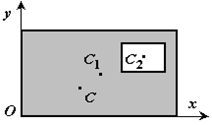
Рисунок 1.9

11. Основные понятия кинематики. Кинематика точки. Способы задания движения точки. Скорость и ускорение точки.

Основные понятия кинематики

Кинематика — раздел механики, изучающий движение тел без учета причин, вызвавших это движение.

Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.

Механическое движение — это изменение положения тел (или частей тела) относительно друг друга в пространстве с течением времени.

Для описания механического движения надо выбрать систему отсчета.

Тело отсчета — тело (или группа тел), принимаемое в данном случае за неподвижное, относительно которого рассматривается движение других тел.

Система отсчета — это система координат, связанная с телом отсчета, и выбранный способ измерения времени (рис. 1).

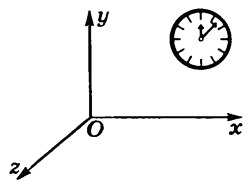
Рис. 1

Положение тела можно определить с помощью радиуса-вектора r⃗ r→ или с помощью координат.

Радиус-вектор r⃗ r→ точки Μ — направленный отрезок прямой, соединяющий начало отсчета О с точкой Μ (рис. 2).

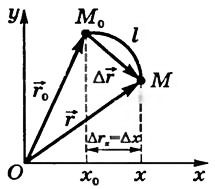
Рис. 2

Координата x точки Μ — это проекция конца радиуса-вектора точки Μ на ось Ох. Обычно пользуются прямоугольной системой ко ординат. В этом случае положение точки Μ на линии, плоскости и в пространстве определяют соответственно одним (x), двумя (х, у) и тремя (х, у, z) числами — координатами (рис. 3).

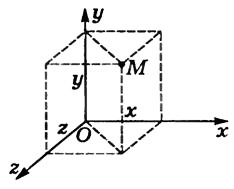
Рис. 3

В элементарном курсе физики изучают кинематику движения материальной точки.

Материальная точка — тело, размерами которого в данных условиях можно пренебречь.

Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно.

Поступательным называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движении все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.

В дальнейшем под словом "тело" будем понимать "материальная точка".

Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. На практике форму траектории задают с помощью математических формул (y = f(x) — уравнение траектории) или изображают на рисунке. Вид траектории зависит от выбора системы отсчета. Например, траекторией тела, свободно падающего в вагоне, который движется равномерно и прямолинейно, является прямая вертикальная линия в системе отсчета, связанной с вагоном, и парабола в системе отсчета, связанной с Землей.

В зависимости от вида траектории различают прямолинейное и криволинейное движение.

Путь s — скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен: s > 0.

Перемещение Δr⃗ Δr→ тела за определенный промежуток времени — направленный отрезок прямой, соединяющий начальное (точка M₀) и конечное (точка М) положение тела (см. рис. 2):

Δr⃗ =r⃗ −r⃗ 0, Δr→=r→−r→0,

где r⃗ r→ и r⃗ 0 r→0 — радиусы-векторы тела в эти моменты времени.

Проекция перемещения на ось Ox

Δrx=Δx=x−x0 Δrx=Δx=x−x0

, где x₀ и x — координаты тела в начальный и конечный моменты времени.

Модуль перемещения не может быть больше пути

|Δr⃗ |≤s |Δr→|≤s

.

Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.

Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:

r⃗ =r⃗ 0+Δr⃗ ; r→=r→0+Δr→;

{x=x0+Δrx;y=y0+Δry. {x=x0+Δrx;y=y0+Δry.

Скорость — мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.

Средняя скорость hυ⃗ i hυ→i — векторная физическая величина, численно равная отношению перемещения к промежутку времени, за который оно произошло, и направленная вдоль перемещения (рис. 4):

hυ⃗ i=Δr⃗ Δt;hυ⃗ i⇈Δr⃗ . hυ→i=Δr→Δt;hυ→i⇈Δr→.

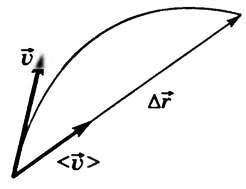
Рис. 4

В СИ единицей скорости является метр в секунду (м/с).

Средняя скорость, найденная по этой формуле, характеризует движение только на том участке траектории, для которого она определена. На другом участке траектории она может быть другой.

Иногда пользуются средней скоростью пути

hυi=sΔt hυi=sΔt

, где s — путь, пройденный за промежуток времени Δt. Средняя скорость пути — это скалярная величина.

Мгновенная скорость υ⃗ υ→ тела — скорость тела в данный момент времени (или в данной точке траектории). Она равна пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени υ⃗ =limΔt→0Δr⃗ Δt=r⃗ ′ υ→=limΔt→0Δr→Δt=r→ ′. Здесь r⃗ ′ r→ ′ — производная от радиуса-вектора по времени.

В проекции на ось Ох:

υx=limΔt→0ΔxΔt=x′. υx=limΔt→0ΔxΔt=x′.

Мгновенная скорость тела направлена по касательной к траектории в каждой ее точке в сторону движения (см. рис. 4).

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени.

Среднее ускорение — физическая величина, численно равная отношению изменения скорости ко времени, за которое оно произошло:

ha⃗ i=Δυ⃗ Δt=υ⃗ −υ⃗ 0Δt. ha→i=Δυ→Δt=υ→−υ→0Δt.

Вектор ha⃗ i ha→i направлен параллельно вектору изменения скорости Δυ⃗ Δυ→ ( ha⃗ i⇈Δυ⃗ ha→i⇈Δυ→) в сторону вогнутости траектории (рис. 5).

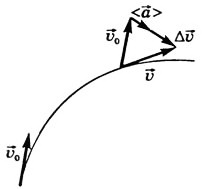
Рис. 5

Мгновенное ускорение:

a⃗ =limΔt→0Δυ⃗ Δt=υ⃗ ′. a→=limΔt→0Δυ→Δt=υ→ ′.

В СИ единицей ускорения является метр на секунду в квадрате (м/с²).

В общем случае мгновенное ускорение направлено под углом к скорости. Зная траекторию, можно определить направление скорости, но не ускорения. Направление ускорения определяется направлением равнодействующей сил, действующих на тело.

При прямолинейном движении с возрастающей по модулю скоростью (рис. 6, а) векторы a⃗ a→ и υ⃗ 0 υ→0 сонаправлены ( a⃗ ⇈υ⃗ 0 a→⇈υ→0) и проекция ускорения на направление движения положительна.

При прямолинейном движении с убывающей по модулю скоростью (рис. 6, б) направления векторов a⃗ a→ и υ⃗ 0 υ→0 противоположны ( a⃗ ↑↓υ⃗ 0 a→↑↓υ→0) и проекция ускорения на направление движения отрицательна.

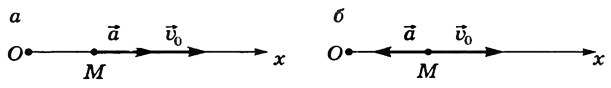
Рис. 6

Вектор a⃗ a→ при криволинейном движении можно разложить на две составляющие, направленные вдоль скорости a⃗ τ a→τ и перпендикулярно скорости a⃗ n a→n (рис. 1.7), a⃗ τ a→τ — тангенциальное ускорение, характеризующее быстроту изменения модуля скорости при криволинейном движении, a⃗ n a→n — нормальное ускорение, характеризующее быстроту изменения направления вектора скорости при криволинейном движении Модуль ускорения a=a2τ+a2n−−−−−−√ a=aτ2+an2.

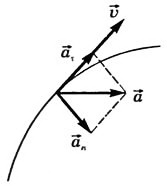
Рис. 7

Способы задания движения точки

Для задания движения точки можно применять один из следую­щих трех способов:

1) векторный, 2) координатный, 3) естественный.

1. Векторный способ задания движения точки.

Пусть точка М движется по отношению к некоторой си­стеме отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор 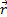, проведенный из на­чала координат О в точку М (рис. 3).

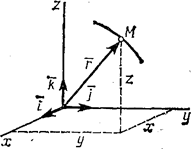
Рис.3

При движении точки М вектор 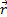будет с течением времени изме­няться и по модулю, и по направлению. Следовательно, 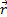является переменным вектором (вектором-функцией), зависящим от аргу­мента t:

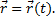
Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор 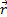и найти положение движущейся точки.

Геометрическое место концов вектора 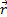, т.е. годографэтого вектора, определяет траекторию движущейся точки.

2. Координатный способ задания движе­ния точки.

Положение точки можно непосредственно опре­делять ее декартовыми координатами х, у, z (рис.3), которые при движении точки будут с течением времени изменяться. Чтобы знать закон дви­жения точки, т.е. ее положение в пространстве в любой момент вре­мени, надо знать значения координат точки для каждого момента времени, т.е. знать зависимости

x=f₁(t), y=f₂(t), z=f₃(t).

Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.

Чтобы получить уравнение траектории надо из уравнений движения исключить параметр t.

Нетрудно установить зависимость между векторным и координатным способами задания движения.

Разложим вектор 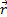на составляющие по осям координат:

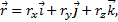
где r_x, r_y, r_z - проекции вектора на оси; 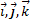– единичные векторы направленные по осям, орты осей.

Так как начало 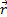вектора находится в начале координат, то проекции вектора будут равны координатам точки M. Поэтому

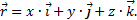
Если движение точки задано в полярных координатах

r=r(t), φ = φ(t),

где r — полярный радиус, φ — угол между полярной осью и по­лярным радиусом, то данные уравнения выражают уравнение траекто­рии точки. Исключив параметр t, получим

r = r(φ).

Пример 1.Движение точки задано уравнениями

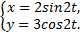
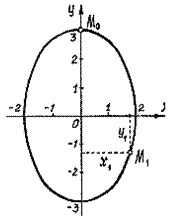
Рис.4

Чтобы исключить время, параметр t, найдём из первого уравнения sin2t=x/2, из второго cos2t=y/3. Затем возведём в квадрат и сложим. Так как sin²2t+cos²2t=1, получим 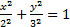. Это уравнение эллипса с полуосями 2 см и 3 см (рис.4).

Начальное положение точки M₀ (при t=0) определяется координатами x₀=0, y₀=3 см.

Через 1 сек. точка будет в положении M₁ с координатами

x₁=2sin2=2∙0,91=1,82 см, y₁=2cos2=3∙(-0,42)= -1,25 см.

Примечание.

Движение точки может быть задано с помощью и других координат. Например, цилиндрических или сферических. Среди них будут не только линейные размеры, но и углы. При необходимости, с заданием движения цилиндрическими и сферическими координатами можно познакомиться по учебникам.

3. Естественный способ задания движе­ния точки.

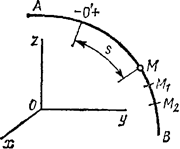
Рис.5

Естественным способом задания движения удобно пользоваться в тех слу­чаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ явля­ется траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.5) Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и отрицатель­ное направления отсчета (как на координат­ной оси).

Тогда положение точки М на тра­ектории будет однозначно определяться криволинейной коорди­натой s, которая равна расстоянию от точки О’ до точки М, изме­ренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения M₁, М₂,... . следовательно, расстояние s будет с течением времени изменяться.

Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость

s=f(t).

Уравнение выражает закон движения точки М вдоль тра­ектории. Функция s= f(t) должна быть однозначной, непрерывной и дифференцируемой.

За положительное направление отсчета дуговой координаты s принимают направление движения точки в момент, когда она занимает положение О. Cледует помнить, что уравнение s=f(t) не определяет закон движения точки в пространстве, так как для определения положения точки в пространстве нужно знать еще траекторию точки с начальным положением точки на ней и фиксированное положительное направление. Таким образом, движение точки считается заданным естественным способом, если известна траектория и уравнение (или закон) движения точки по траектории.

Важно заметить, что дуговая координата точки s отлична от пройденного точкой по траектории пути σ. При своем движении точка проходит некоторый путь σ, которой является функцией времени t. Однако пройденный путь σ совпадает с расстоянием s лишь тогда, когда функция s = f(t) монотонно изменяется со временем, т.е. при движении точки в одном направлении. Допустим, что точка М переходит из М₁ в М₂. Положению точки в М₁ соответствует время t₁, а положению точки в М₂ - время t₂. Разложим промежуток времени t₂- t₁ на весьма малые промежутки времени ∆t₁ (i = 1,2, …n) так, чтобы в каждый из них точка совершала движение в одном направлении. Соответствующее приращение дуговой координаты обозначим ∆s_i. Пройденной точкой путь σ будет положительной величиной:

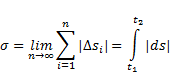
Если движение точки задано координатным способом, то пройденный путь определяется по формуле

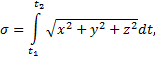
так как

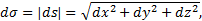
где dx=xdt, dy= ydt, dz=zdt.

Следовательно,

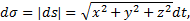
Пример 2. Точка движется по прямой линии, по закону s=2t+3 (см) (рис. 6).

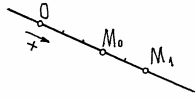
Рис.6

В начале движения, при t=0 s=OM₀=s₀=3 см. Положение точки M₀ назы­вается начальным положением. При t=1 с, s=OM₁=5 см.

Конечно, за 1 сек. точка прошла расстоя­ние M₀M₁=2см.Так что s – это не путь пройденный точ­кой, а расстояние от начала отсчёта до точки.

Вектор скорости точки

Одной из основных кинематических характеристик движе­ния точки является векторная величина, называемая скоростью точки. Понятие скорости точки в равномерном прямолинейном движении относится к числу элементарных понятий.

Скорость - мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.

Единица измерения скорости – м/с. Часто используют и другие единицы, например, км/ч: 1 км/час=1/3,6 м/с.

Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным.

Для равномерно-прямолинейного движения

∆r=v∆t, (1)

где v– постоянный вектор.

Вектор vназывается скоростью прямолинейного и равномерного движения полностью его определяет.

Из соотношения (1) видно, что скорость прямолинейного и равномерного движения является физической величиной, определяющей перемещение точки за единицу времени. Из (1) имеем

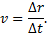
Направление вектора v указано на рис. 6.1.

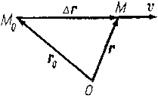
Рис.6.1

При неравномерном движении эта формула не годится. Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени.

Пусть движущаяся точка находится в момент времени t в положении М, определяемом радиусом-векто­ром 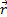, а в момент t₁ приходит в положение M₁ определяемое векто­ром 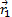(рис.7). Тогда перемещение точки за промежуток времени ∆t=t₁-t определяется вектором 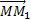который будем называть вектором перемещения точки. Из треугольника ОММ₁ видно, что 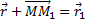; следовательно,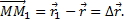

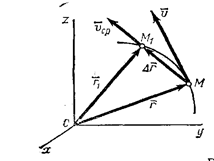
Рис. 7

Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую сред­ней по модулю и направлению скоростью точки за промежуток времени ∆t:

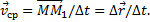
Скоростью точки в данный момент времени t называется векторная величина v, к которой стремится средняя скорость v_ср при стремлении промежутка времени ∆t к нулю:

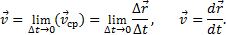
Итак, вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени.

Так как предельным направлением секущей ММ₁ является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.

Определение скорости точки при координатном способе задания движения

Вектор скорости точки 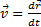, учитывая, что r_x=x, r_y=y, r_z=z, найдем:

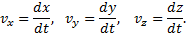
Таким образом, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.

Зная проекции скорости, найдем ее модуль и направление (т.е. углы α, β, γ, которые вектор v образует с координатными осями) по формулам

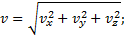
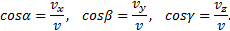
Итак, численная величина скорости точки в данный момент времени равна первой производной от расстояния (криволинейной координаты) s точки по времени.

Направлен вектор скорости по касательной к траектории, кото­рая нам наперед известна.

Определение скорости точки при естественном способе задания движения

Величину скорости можно определить как предел (∆r – длина хорды ММ₁):

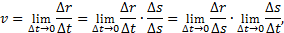
где ∆s – длина дуги ММ₁. Первый предел равен единице, второй предел – производная ds/dt.

Следовательно, скорость точки есть первая производная по времени от закона движения:

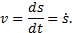
Направлен вектор скорости, как было установлено ранее, по касательной к траектории. Если величина скорости в данный момент будет больше нуля, то вектор скорости направляется в положительном направлении

Вектор ускорения точки

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени.

В СИ единицей ускорения является метр на секунду в квадрате .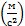

Пусть в некоторый момент времени t движущаяся точка находится в положении М и имеет скорость v, а в момент t₁ приходит в положение M₁ и имеет скорость v₁ (рис. 8).

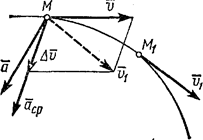
Рис.8

Тогда за промежуток времени ∆t=t₁-t скорость точки получает приращение 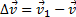. Для построения вектора 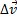отложим от точки М вектор, равный v₁, и построим параллелограмм, в котором диагональю будет 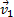, a одной из сторон 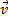. Тогда, очевидно, вторая сторона и будет изображать вектор 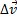. Заметим, что вектор 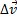всегда направлен в сторону вог­нутости траектории.

Отношение приращения вектора скорости 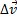к соответствующему про­межутку времени ∆t определяет век­тор среднего ускорения точки за этот промежуток времени:

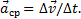
Вектор среднего ускорения имеет то же направление, что и век­тор 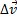, т.е. направлен в сторону вогнутости траектории.

Ускорением точки в данный момент времени t называется век­торная величина 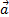, к которой стремится среднее ускорение 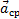при стремлении промежутка времени ∆t к нулю: Вектор ускорения точки в данный момент време­ни равен первой производной от вектора скорости или второй произ­водной от радиуса-вектора точки по времени.

Ускорение точки равно нулю лишь тогда, когда скорость точки v посто­янна как по величине, так и по направлению: это соответствует только прямолинейному и равно­мерному движению.

Найдем, как располагается вектор 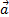по отношению к траекто­рии точки. При прямолинейном движении вектор 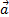направлен вдоль прямой, по которой движется точка.

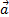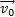При прямолинейном движении с возрастающей по модулю скоростью (рис. 9, а) векторы и сонаправлены ( 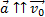) и проекция ускорения на направление движения положительна.

При прямолинейном движении с убывающей по модулю скоростью (рис. 9, б) направления векторов 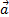и 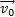противоположны ( 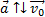) и проекция ускорения на направление движения отрицательна.

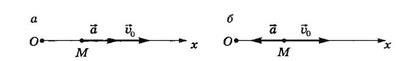
Рис.9

Если траекторией точки явля­ется плоская кривая, то вектор ускорения 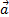, так же как и вектор 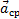, лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория не является плоской кривой, то вектор 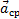на­правлен в сторону вогнутости траектории и лежит в плоскости, про­ходящей через касательную к траектории в точке М и прямую, па­раллельную касательной в соседней точке M₁ (рис. 8). В пределе, когда точка М стремится к М, эта плоскость занимает положение так называемой соприкасающейся плоскости, т.е. плоскости, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении движущейся точки. Следовательно, в общем случае вектор ускорения 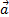лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.

Определение ускорения при координатном способе задания движения

Вектор ускорения точки 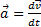в проекции на оси получаем:

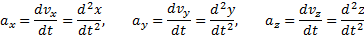
Или

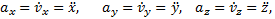
т.е. проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул

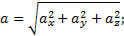
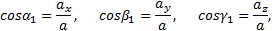
где α₁, β₁, γ₁ - углы, образуемые вектором ускорения с координатными осями.

Пример 3. Движение точки задано уравнениями x=2t, y=3-4t².

Из первого уравнения t=x/2. Подставив во второе, получим уравнение траектории: y=3-x²

Это уравнение параболы. В на­чале движения, при t=0, точка находи­лась на самом верху, в положении M₀ (x₀=0, y₀=3 см).

А, например, при t =0,5 c она будет в положении M с координатами x₁=1 см; y₁=2 см.

Проекции скорости на оси v_x= 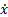=2см∙с^-1, v_y= 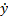=-8t см∙с^-1.

При t =0,5 c, v_x=2см∙с^-1, v_y=-4 см∙с^-1.

И модуль скорости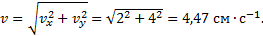

Составляющие скорости по осям и вектор её показаны в масштабе на рис. 10.

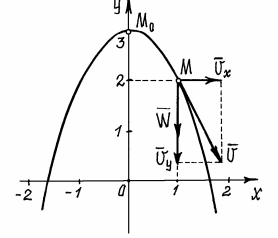
Рис.10

Проекции ускорения a_x= 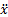=0, a_y= 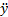=-8 см∙с^-2. Так как проекция вектора ускорения на ось x равна нулю, а на ось y – отрица­тельна, то вектор ускорения на­правлен верти­кально вниз, и величина его постоянна, не за­висит от времени.