Пара сил. Момент пары сил. Теоремы о пары.

Пара сил. Момент пары сил

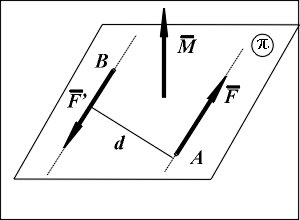Парой сил называется приложенная к твердому телу система двух сил (F,F') , равных по модулю, параллельных и направленных в противоположные стороны:

F = -F'; F=F'.

Расстояние d между линиями действия сил пары называется плечом пары; плоскость 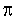, в которой действуют силы пары, называется плоскостью действия пары. Совокупность нескольких пар, действующих на тело, называется системой пар.

Пара сил не имеет равнодействующей. Она стремится сообщить телу некоторое вращение. Вращательный эффект пары характеризуется векторной величиной, называемой моментом пары. Момент пары сил относительно точки O

M_O(F,F') = M_O(F) + M_O(F')

не зависит от выбора точки O и равен моменту одной из сил пары относительно точки приложения другой силы

M(F,F') = M_A(F') = M_B(F) .

Момент пары сил M перпендикулярен плоскости действия пары, направлен по правилу правого винта и равен по модулю произведению модуля любой из сил на плечо пары: M = F · d.

Векторный момент пары сил может быть приложен в любой точке пространства, т.е. является свободным вектором.

Две пары сил, имеющие одинаковые векторные моменты, эквивалентны, т.е. оказывают на тело одинаковое механическое действие.

Эквивалентность пар: действие пары сил на твердое тело не изменится, если

• переместить пару в другое положение в плоскости ее действия;
• плоскость ее действия переместить параллельно самой себе;
• любым образом изменить модули сил и плечо пары, сохранив неизменным их произведение, т.е. момент пары M=F · d.

Сложение пар сил: система n пар сил с моментами M₁,M₂,...,M_n эквивалентна одной паре с моментом M, равным векторной сумме моментов этих пар: M = 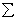M_k.

Условие равновесия системы пар, приложенных к твердому телу: M = 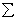M_k=0.

Теорема 1.Действие пары сил на твердое тело не изменится, если пару перенести в любое место плоскости ее действия и изменить модули сил и величину плеча так, чтобы момент пары не изменился.

Доказательство

Рассмотрим пару сил 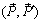и точки C, D, произвольно выбранные

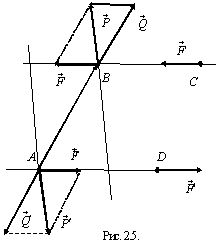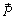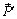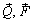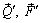в плоскости ее действия (рис. 2.5). Проведем через точки C и D две параллельные прямые до пересечения с линиями действия сил пары в точкахA и B, где приложим силы и . Разложим их на составляющие и . На основании аксиомы 1 система 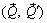~ 0 и в соответствии с аксиомой 2 может быть отброшена, т.е.

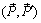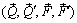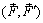~ ~ . Силы 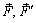, образующие пару сил, перенесем вдоль их линий действия в точки C и D. Покажем, что моменты эквивалентных пар 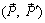и 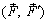одинаковы:

.

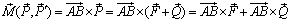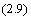
Так как векторы 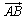и 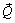коллинеарны, векторное произведение 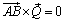и на основании (2.9) получим

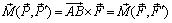
Теорема доказана.

Теорема 2. Действие пары на твердое тело не изменится, если ее перенести в любую плоскость, параллельную плоскости ее действия.

Доказательство

Рассмотрим пару сил 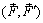, действующую в плоскости I (рис. 2.6). В плоскости II, параллельной плоскости I, отложим отрезок CD (CD || AB, CD = АВ). Приложим в точках Cи D уравновешенные системы сил:

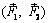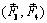~ 0, ~ 0, , .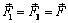

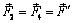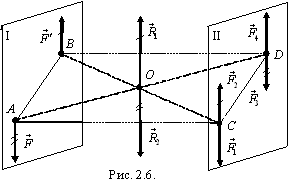
Заменим равные параллельные силы 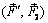их равнодействующей 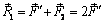, приложенной в середине отрезка BC, а силы 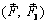– равнодействующей 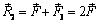, приложенной в середине отрезка AD. Так как ABСD – параллелограмм, точки приложения сил 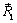и 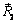, равных по модулю и противоположно направленных, совпадают с точкой пересечения O диагоналей параллелограмма, а сами силы образуют уравновешенную систему сил, которую можно отбросить.

Оставшиеся силы 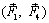образуют пару сил, действующую в плоскости II, геометрически равную исходной паре сил 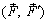и эквивалентную ей. Действительно, описанные преобразования можно записать так:

~ ~ ~ ,

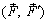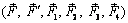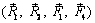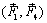что и доказывает утверждение теоремы.

Во всех ситуациях, описанных в теоремах 1 и 2, исходная и преобразованная пары сил эквивалентны и имеют равные моменты. Таким образом, момент пары является свободным вектором, полностью и однозначно характеризующим ее действие на твердое тело, поэтому справедлива следующая теорема.

Теорема 3. Две пары сил, имеющие равные моменты, эквивалентны.

Теорема 4. Система пар сил, действующих на твердое тело, эквивалентна одной паре, момент которой равен сумме моментов всех пар системы.

Доказательство

Рассмотрим две пары сил 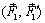и 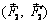, лежащих в пересекающихся плоскостях I и II (рис. 2.7). Выберем на линии пересечения плоскостей точки A, B и, пользуясь теоремой 1, перенесем рассматриваемые пары сил, приводя их к плечу AB. Преобразованные пары сил 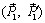и 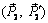должны иметь такие же моменты, как и исходные:

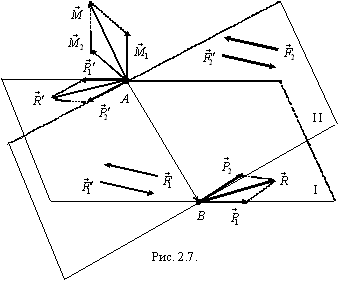
Используя аксиому 3, сложим силы, приложенные в точках B и A:

.

Так как 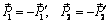, получим 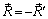, т.е. силы 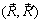образуют пару сил. Ее момент

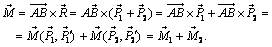
Таким образом, для двух пар сил, лежащих в пересекающихся плоскостях, теорема доказана. Очевидно, что доказательство справедливо и для совпадающих плоскостей I и II, т.е. если пары сил лежат в одной плоскости. Пары, лежащие в параллельных плоскостях, на основании теоремы 2 могут быть перенесены в одну плоскость.

Если на тело действует система пар с моментами 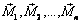то, последовательно применяя результат теоремы, доказанной для двух пар, приходим к выводу, что данная система пар эквивалентна одной паре, момент которой

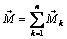. (2.10)

Теорема доказана.