Нелинейная эмпирическая регрессия

Многие экономические зависимости не являются линейными по своей сути, и поэтому их моделирование линейными уравне­ниями регрессии не дает положительного резуль­тата. Нелинейность может проявляться как относительно переменных, так и относительно входящих в функцию коэффициентов.

Оценка параметров нелинейной регрессии по переменным, включенным в анализ, но линейным по оцениваемым параметрам, проводится с помощью МНК путем решения системы линейных алгебраических уравнений.

1. Степенные модели вида , где – параметры модели.

Рис. 2. Зависимость ,

Прологарифмируем выражение : и выполняем замену , , , . Тогда получим . Полученная модель является линейной. Коэффициент определяет эластичность пе­ременной Y по переменной X и является константой.

Данная модель легко обобщается на большее число переменных. Например, . Здесь коэффициенты и являются эластичноcтями переменной Y по переменным X₁ и X₂ соответственно.

2. Показательная модель , .

Рис. 3. Зависимость ,

Прологарифмируем выражение : .

Выполним замену , , , , получим линейную модель .

3. Логарифмические модели – это модели вида . Они сводится к линейной модели заменой .

a > 0

Рис. 4. Зависимость

4. Обратная модель. Модель вида заменой , приводится к линейной модели . Модель вида заменой ; приводится к линейной модели .

Рис. 5. Зависимость Рис. 6. Зависимость

Пример 4.По десяти районам за год известны доля расходов на покупку продовольственных товаров в общих расходах K(%)и средненедельная зарплата t одного работающего (ден. ед.). Получены следующие экспериментальные данные зависимости между и , представленные в табл. 4.

Таблица 4

t		5,6		6,4	6,8	7,2	7,6		8,4	8,8
K	10,4	14,4	17,1	22,5	25,9	33,1	40,4		59,2	74,1

Найти эмпирическую функциональную зависимость .

Решение.

На плоскости переменных 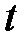и 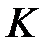построим точки 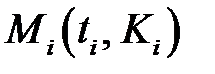и соединим их плавной кривой (рис. 15).

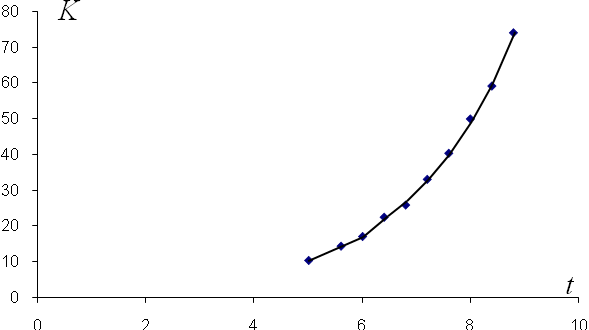
Рис. 15. Диаграмма исходных данных

По виду полученной диаграммы предполагаем, что для данного случая можно использовать зависимост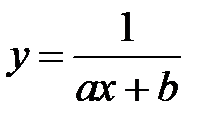и или .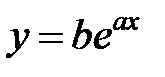

Рассмотрим зависимость

.

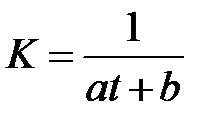Используя преобразование

,

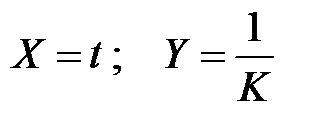зависимость 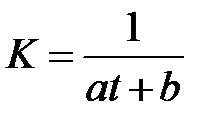преобразуем в линейную 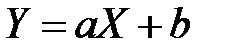. Найдем значения новых переменных X и Y и результаты расчетов занесем в табл. 5.

Таблица 5

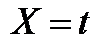	5,0	5,6	6,0	6,4	6,8	7,2	7,6	8,0	8,4	8,8
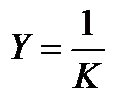	0,096	0,069	0,058	0,044	0,039	0,030	0,024	0,020	0,016	0,013

Построив на плоскости OXY точки 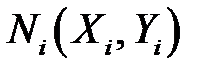, 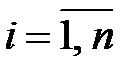(рис. 16), мы видим, что они расположены вдоль некоторой кривой, а не прямой линии.

Рис. 16.

Предположим теперь, что зависимость описывается формулой 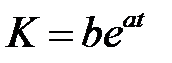. Используя преобразование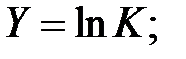 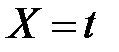, получим

.

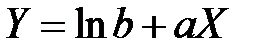Найдем значения новых переменных X и Y по формулам 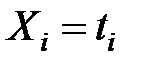; 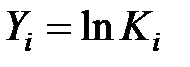и запишем в табл. 6

Таблица 6

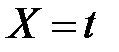	5,0	5,6	6,0	6,4	6,8	7,2	7,6	8,0	8,4	8,8
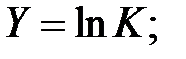	2,34	2,67	2,84	3,11	3,25	3,50	3,70	3,91	4,08	4,31

На плоскости XOY построим точки 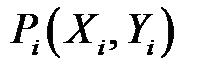, 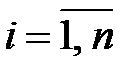. Как видно на (рис. 17), они расположены вдоль некоторой прямой линии, следовательно, выбранная зависимость лучше соответствует исходным данным.

Рис. 17.

Параметры 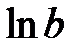и 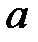найдем МНК. Для вычисления коэффициентов системы составим табл. 7.

Таблица 7

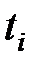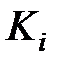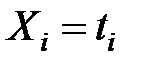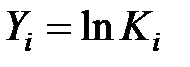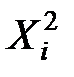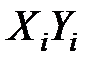	10,4		2,3418		11,709
5,6	14,4	5,6	2,6672	31,36	14,936
	17,1		2,8391		17,034
6,4	22,5	6,4	3,1135	40,96	19,926
6,8	25,9	6,8	3,2542	46,24	22,129
7,2	33,1	7,2	3,4995	51,84	25,197
7,6	40,4	7,6	3,6988	57,76	28,111
			3,912		31,296
8,4	59,2	8,4	4,0809	70,56	34,28
8,8	74,1	8,8	4,3054	77,44	37,888
	∑	69,8	33,713	501,16	242,51

Составим нормальную систему уравнений

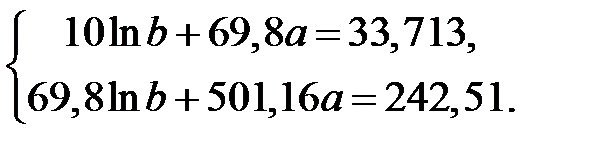
Решая ее, находим 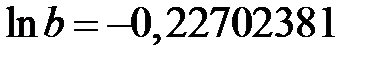и 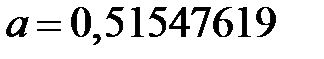. Отсюда получаем значение параметра 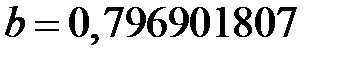. Таким образом, исходную зависимость можно описать функцией .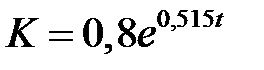