Понятие о регрессионной модели
Уравнением (теоретическим) регрессии Y на X называется уравнение 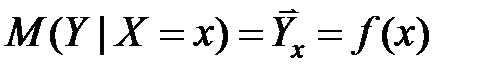 . Функция ¦(x) называется (теоретической) регрессией Y на X а ее график – линией регрессии СВ Y на СВ X. При этом X является независимой (объясняющей) переменной, Y — зависимой (объясняемой) переменной. При рассмотрении зависимости двух СВ говорят о парной регрессии.
. Функция ¦(x) называется (теоретической) регрессией Y на X а ее график – линией регрессии СВ Y на СВ X. При этом X является независимой (объясняющей) переменной, Y — зависимой (объясняемой) переменной. При рассмотрении зависимости двух СВ говорят о парной регрессии.
Зависимость нескольких переменных, выражаемая функцией
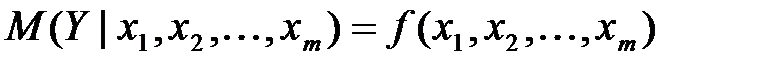 ,
,
где 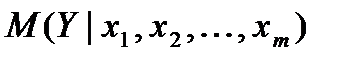 – условное математическое ожидание (математическое ожидание СВ Y при условии, что СВ X в i-м наблюдении приняла значения
– условное математическое ожидание (математическое ожидание СВ Y при условии, что СВ X в i-м наблюдении приняла значения 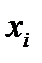 ), называют множественной регрессией.
), называют множественной регрессией.
Поскольку реальные значения зависимой переменной не всегда совпадают с ее условными математическими ожиданиями и могут быть различными при одном и том же значении объясняющей переменной (наборе объясняющих переменных), фактическая зависимость должна учитывать ошибку (погрешность) ε, которая также является СВ. Таким образом, связи между зависимой и объясняющей(ими) переменными можно описать соотношениями
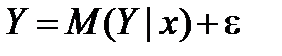
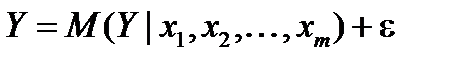
Задачи корреляционно-регрессионного анализа
Основные задачи корреляционно-регрессионного анализа:
1. Установление формы корреляционной связи, т. е. установление вида функции регрессии (линейная, квадратичная, показательная и т. д.).
2. Оценка тесноты корреляционной связи Y и X, которая оценивается величиной рассеяния значений СВ Y около 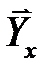 . Большое рассеяние означает слабую зависимость Y от X либо вообще ее отсутствие. Малое рассеяние указывает на существование достаточно сильной зависимости Y от X.
. Большое рассеяние означает слабую зависимость Y от X либо вообще ее отсутствие. Малое рассеяние указывает на существование достаточно сильной зависимости Y от X.
3. Оценивание неизвестных параметров регрессионной модели, проверка гипотез об их значимости и адекватности модели рассматриваемому экономическому объекту.
Выбор формулы связи переменных называется спецификацией уравнения регрессии. В случае парной регрессии выбор формулы обычно осуществляется по графическому изображению реальных статистических данных.
Пример 1.Для анализа зависимости инвестиций (y) предприятия от объемов (x) производства исследуются данные 12 однотипных предприятий. Данные приведены в табл 2.
Таблица 2
| Предприятие | ||||||||||||
Инвестиции ( 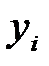 ), тыс. у.е. ), тыс. у.е. | ||||||||||||
Объем пр-ва ( 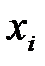 ), млрд. шт. ), млрд. шт. |
Необходимо построить корреляционное поле.
Решение. Построим корреляционное поле (рис. 14).
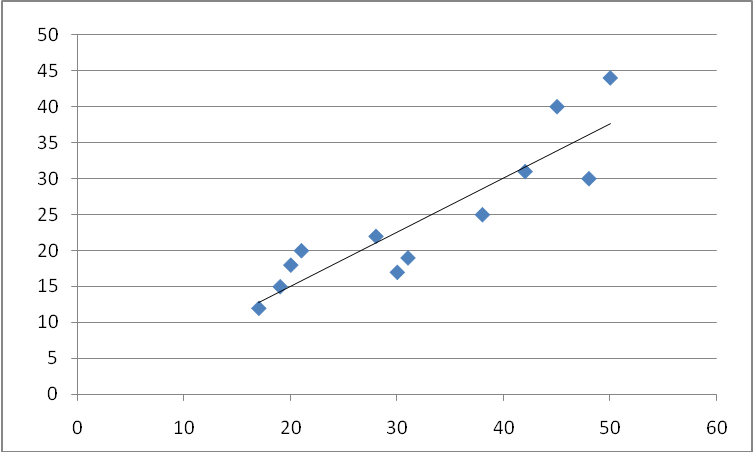
Рис. 14. Корреляционное поле
По расположению точек на корреляционном поле полагаем, что зависимость между X и Y близка к линейной.
Линейная парная регрессия
По выборке ограниченного объема можно искать регрессионную зависимость в определенном виде, например, в виде линейной зависимости:
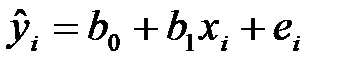 (эмпирическое линейное уравнение регрессии), (эмпирическое линейное уравнение регрессии), | (1) |
где 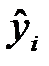 – оценка условного математического ожидания
– оценка условного математического ожидания 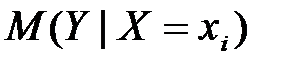 ;
; 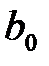 и
и 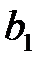 – оценки неизвестных параметров, называемые эмпирическими коэффициентами линейной регрессии, отклонение
– оценки неизвестных параметров, называемые эмпирическими коэффициентами линейной регрессии, отклонение 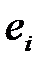 – оценка теоретического случайного отклонения
– оценка теоретического случайного отклонения 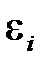 .
.
Модель линейной регрессии (линейное уравнение) является наиболее распространенным (и простым) видом зависимости между экономическими переменными. Кроме того, построенное линейное уравнение может служить начальным этапом эконометрического анализа.
Задачи линейного регрессионного анализа (см. Пример 2):
1. По имеющимся статистическим данным 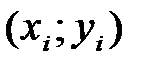 ,
, 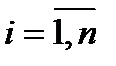 получить наилучшие оценки неизвестных параметров;
получить наилучшие оценки неизвестных параметров;
2. Проверить статистические гипотезы о параметрах модели;
3. Проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений).
Метод наименьших квадратов
Различные выборки из одной и той же генеральной совокупности обычно приводят к определению отличающихся друг от друга оценок. Требуется по конкретной выборке 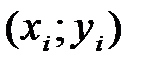 ,
, 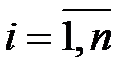 , найти оценки
, найти оценки 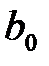 и
и 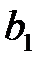 неизвестных параметров уравнения (1) так, чтобы соответствующая линия регрессии (прямая) являлась бы наилучшей в определенном смысле среди всех других прямых. Другими словами, построенная прямая должна быть «ближайшей» к точкам наблюдений по их совокупности. Мерами качества найденных оценок могут служить определенные функции отклонений (невязок)
неизвестных параметров уравнения (1) так, чтобы соответствующая линия регрессии (прямая) являлась бы наилучшей в определенном смысле среди всех других прямых. Другими словами, построенная прямая должна быть «ближайшей» к точкам наблюдений по их совокупности. Мерами качества найденных оценок могут служить определенные функции отклонений (невязок) 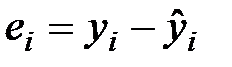 ,
, 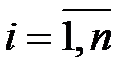 .
.
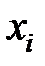 |
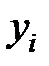 |
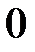 |
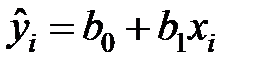 |
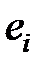 |
Рис. 1
Самым распространенным является метод наименьших квадратов (МНК)нахождения коэффициентов (оценок) 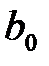 и
и 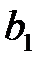 уравнения эмпирической линейной регрессии. Согласно МНК эти коэффициенты выбираются таким образом, чтобы минимизировать функцию (сумму квадратов отклонений):
уравнения эмпирической линейной регрессии. Согласно МНК эти коэффициенты выбираются таким образом, чтобы минимизировать функцию (сумму квадратов отклонений):
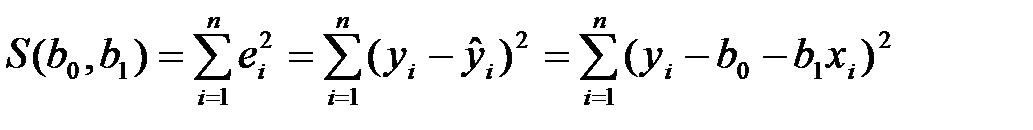 .
.
Необходимым условием минимума данной функции является равенство нулю ее частных производных по параметрам 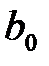 и
и 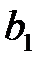 , откуда для определения параметров линейной регрессии получаем линейную систему алгебраических уравнений:
, откуда для определения параметров линейной регрессии получаем линейную систему алгебраических уравнений:
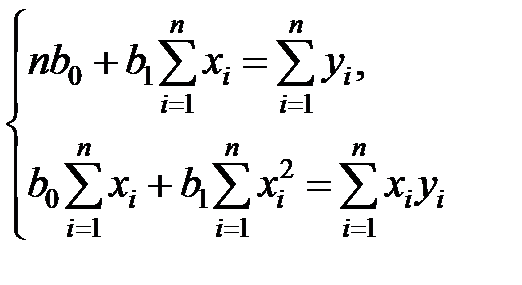
Коэффициент 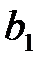 называется выборочным коэффициентом регрессии Y на X. Он показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной X на одну единицу.
называется выборочным коэффициентом регрессии Y на X. Он показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной X на одну единицу.
Коэффициент 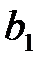 нельзя непосредственно использовать для оценки влияния факторного признака x на результативный признак y из-за различия единиц измерения исследуемых показателей. Для этих целей применяется коэффициент эластичности
нельзя непосредственно использовать для оценки влияния факторного признака x на результативный признак y из-за различия единиц измерения исследуемых показателей. Для этих целей применяется коэффициент эластичности
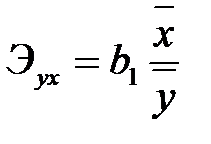 ,
,
где 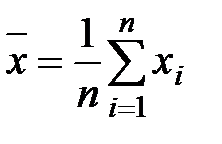 ,
, 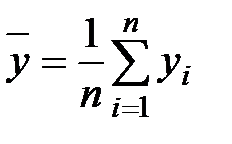 – средние значения независимой и зависимой переменной.
– средние значения независимой и зависимой переменной.
Коэффициент эластичности показывает, на сколько процентов изменяется результативный признак y при изменении факторного признака x на один процент.
Основные положения регрессионного анализа. Теорема Гаусса-Маркова. Оценки параметров регрессионной модели и их свойства
МНК обеспечивает оптимальные свойства оценкам лишь при выполнении следующих основных предпосылок регрессионного анализа:
1. Математическое ожидание случайного отклонения 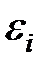 равно 0:
равно 0: 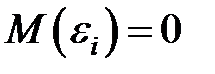 для всех наблюдений, т.е. случайное отклонение в среднем не оказывает влияния на зависимую переменную.
для всех наблюдений, т.е. случайное отклонение в среднем не оказывает влияния на зависимую переменную.
2. Дисперсия случайного отклонения 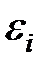 постоянна для любого
постоянна для любого 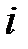 :
: 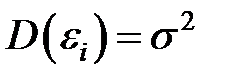 (условие гомоскедастичности — постоянства дисперсий).
(условие гомоскедастичности — постоянства дисперсий).
3. Случайные отклонения 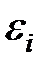 и
и 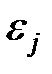 являются независимыми друг от друга, если
являются независимыми друг от друга, если 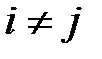 . Если это условие выполняется, то говорят об отсутствии автокорреляции. С учетом выполнения условия 1
. Если это условие выполняется, то говорят об отсутствии автокорреляции. С учетом выполнения условия 1 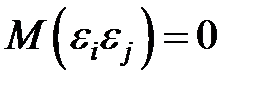 , если
, если 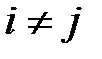 .
.
4. Случайное отклонение независимо от объясняющих переменных. Обычно это условие выполняется автоматически, если объясняющая переменная 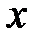 не является случайной в данной модели.
не является случайной в данной модели.
5. Случайное отклонение 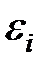 есть нормально распределенная случайная величина.
есть нормально распределенная случайная величина.
Теорема Гаусса-Маркова. Если регрессионная модель удовлетворяет предпосылкам 1—4, то оценки 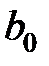 и
и 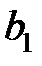 имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.
имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.
Таким образом, оценки 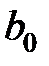 и
и 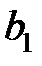 полученные по методу МНК являются:
полученные по методу МНК являются:
Ø несмещенными, так как 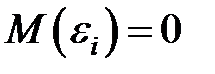 , что говорит об отсутствии систематической ошибки в определении положения линии регрессии,
, что говорит об отсутствии систематической ошибки в определении положения линии регрессии,
Ø состоятельными, так как дисперсия оценок параметров при возрастании числа 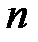 наблюдений стремится к нулю (при увеличении объема выборки надежность оценок увеличивается),
наблюдений стремится к нулю (при увеличении объема выборки надежность оценок увеличивается),
Ø эффективными, т.е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров, линейными относительно величин 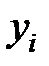 .
.
Требование выполнения предпосылки 5 необходимо для оценки точности уравнения регрессии и его параметров.
Для проверки гипотезы о статистической значимости коэффициента регрессии, т.е. гипотезы 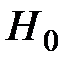 :
: 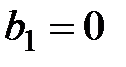 , при конкурирующей (альтернативной) гипотезе
, при конкурирующей (альтернативной) гипотезе 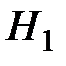 :
: 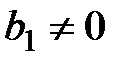 , используется t-статистика:
, используется t-статистика:
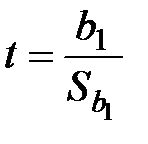 , , |
которая при выполнении исходных предпосылок модели, имеет распределение Стьюдента с числом степеней свободы 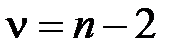 , где
, где 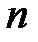 – число наблюдений.
– число наблюдений.
Гипотеза 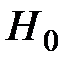 отклоняется, если
отклоняется, если 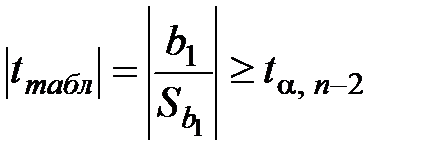 , где
, где 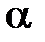 – требуемый уровень значимости, в противном случае – принимается.
– требуемый уровень значимости, в противном случае – принимается.
Если гипотеза 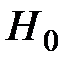 принимается, что дает (эмпирическое) основание полагать, что величина Y не зависит от X. В этом случае говорят, что коэффициент
принимается, что дает (эмпирическое) основание полагать, что величина Y не зависит от X. В этом случае говорят, что коэффициент 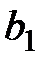 статистически незначим. При отклонении
статистически незначим. При отклонении 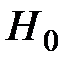 коэффициент
коэффициент 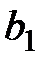 считается статистически значимым, что дает (эмпирическое) основание наличия определенной линейной зависимости между Y и X.
считается статистически значимым, что дает (эмпирическое) основание наличия определенной линейной зависимости между Y и X.
По аналогичной схеме на основе t-статистики проверяется гипотеза о статистической значимости коэффициента 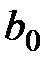 :
:
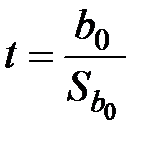 .
.
Для парной регрессии более важным является анализ статистической значимости коэффициента 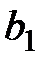 , так как именно он позволяет оценить влияние объясняющей переменной X на зависимую переменную Y.
, так как именно он позволяет оценить влияние объясняющей переменной X на зависимую переменную Y.
Пример 2.Для данных их примера 1: оценить тесноту и направление связи между переменными с помощью коэффициента корреляции; оценить значимость полученного коэффициента корреляции по критерию Стьюдента (уровень значимости 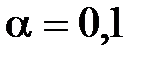 ); найти уравнение регрессии У по X. Сделать выводы.
); найти уравнение регрессии У по X. Сделать выводы.
Решение. Будем искать уравнение регрессии в виде 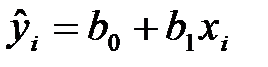 ,
, 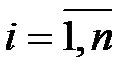 . Оценим тесноту и направление связи между переменными с помощью коэффициента корреляции
. Оценим тесноту и направление связи между переменными с помощью коэффициента корреляции 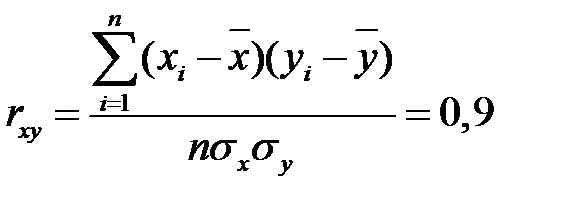 . Поскольку коэффициент корреляции положительный, связь прямая. Коэффициент корреляции близок к единице, связь сильная.
. Поскольку коэффициент корреляции положительный, связь прямая. Коэффициент корреляции близок к единице, связь сильная.
Для проверки значимости коэффициента корреляции используется t-критерий Стьюдента
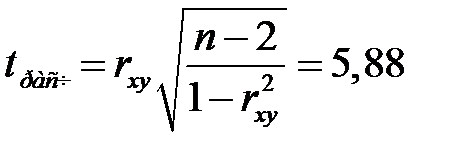 .
.
При уровне значимости 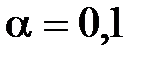 и, учитывая, что в нашем примере количество степеней свободы равно
и, учитывая, что в нашем примере количество степеней свободы равно 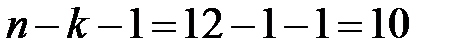 ,
, 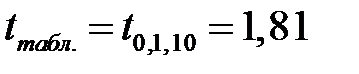 . Так как
. Так как 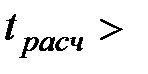
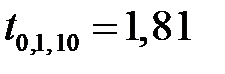 , то значение коэффициента корреляции признается значимым. Парный коэффициент детерминации:
, то значение коэффициента корреляции признается значимым. Парный коэффициент детерминации: 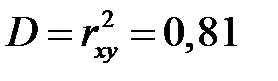 . Это значит, что изменение y на 81% зависит от изменения исследуемых факторов, а на долю других факторов приходится 19% изменения результативного показателя.
. Это значит, что изменение y на 81% зависит от изменения исследуемых факторов, а на долю других факторов приходится 19% изменения результативного показателя.
Найдем уравнение регрессии Y по X. Вычисления по МНК удобно выполнять, используя следующую табл. 3.
Таблица 3
| i | xi | yi | xixi | xiyi |
| сумма | ||||
| среднее | 32,42 | 24,42 |
Согласно МНК, имеем
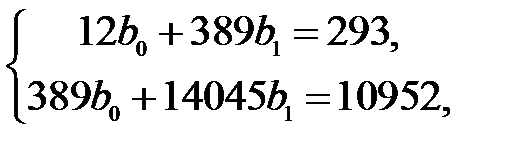
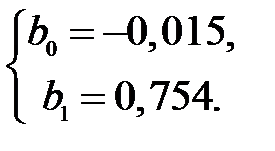
Таким образом, эмпирическое уравнение парной линейной регрессии имеет вид
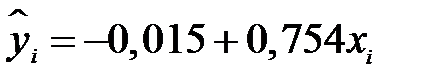 .
.
Изобразим данную прямую на корреляционном поле. Построим эту прямую, например, по следующим двум точкам 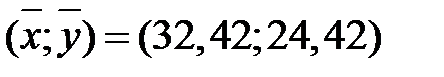 и
и 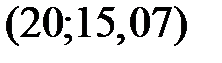 .
.
Коэффициент 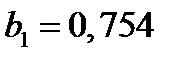 показывает, на какую величину изменятся инвестиции в данное предприятие, если объем производства этого предприятия возрастает на одну единицу.
показывает, на какую величину изменятся инвестиции в данное предприятие, если объем производства этого предприятия возрастает на одну единицу.
Воздействие неучтенных факторов и ошибок наблюдений определяется с помощью дисперсии случайных отклонений 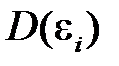 . Несмещенной оценкой этой дисперсии является выборочная остаточная дисперсия.
. Несмещенной оценкой этой дисперсии является выборочная остаточная дисперсия.
Прогнозируемое значении переменнойy вычисляется по формуле
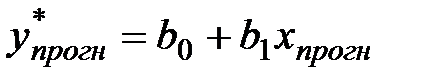 .
.
Данный прогноз является точечным.
