Элементы корреляционно-регрессионного анализа

Теоретический минимум

Основные понятия эконометрики

Эконометрика – наука, объединяющая совокупность математико-статистических методов моделирования и количественного анализа экономических явлений и процессов.

Эконометрика позволяет найти количественное подтверждение (либо не подтверждение) того или иного экономического закона или гипотезы. Одним из важнейших направлений эконометрики является построение прогнозов по различным экономическим показателям.

Задачи эконометрики:

1. Спецификация модели – построение эконометри­ческих моде­лей для эмпирического анализа.

2. Параметризация модели – оценка пара­метров модели.

3. Верификация модели – проверка качества па­раметров модели и самой модели в целом.

4. Прогнозирование модели – составление прогноза и рекомендаций для конкретных экономи­ческих явле­ний по результатам моделирования.

Эконометрическая модель – математическое описание соотношений между входными (объясняющими, независимыми, экзогенными) и выходными (объясняемыми, зависимыми, эндогенными) переменными изучаемого экономического явления или процесса, основанное на реальных статистических данных.

Эконометрические модели условно делят на три класса.

1.Регрессионные модели с одним уравнением. Результативный признак представлен в виде функции факторных признаков 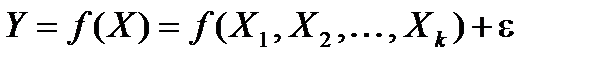, где Y – наблюдаемое значение зависимой эндогенной пе­ременной, которая зависит от значений объясняющих (экзогенных) переменных (факторов); 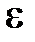– случайная ошибка (возмущение).

Объясняемая переменная Y – случайная величина (СВ) при заданных значениях объясняющих переменных 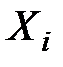, 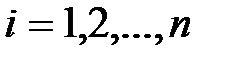. Объясняющие переменные в модели могут также случайный характер. Например, зависимость цены от объема поставки, модель спроса от цены на отдельный товар, от реальных доходов потребителей, модель зависимости объема производства от производственных факторов.

2.Системы одновременных уравнений. Они состоят из уравнений, в которых наряду с факторными признаками включены и результативные признаки, т.е. одни и те же переменные могут одновременно рассматриваются как зависимые переменные в одних уравнениях и как независимые – в других.

3.Модели временных рядов. Результативный признак является функцией времени или переменных, относящихся к другим моментам времени.

В эконометрическом моделировании рассматриваются следующие типы данных:

1. Пространственные данные – набор сведений по разным объектам, взятым за один и тот же период времени (объем производства предприятий региона, численность сотрудников институтов и т.д.).

2. Временные данные – набор сведений, характеризующий один и тот же объект за разные периоды времени (индекс потребительских цен и др.).

Элементы корреляционно-регрессионного анализа

Основные понятия корреляционного анализа

Корреляционный анализ – раздел математической статистики, изучает силу (тесноту) связи между признаками (двумя признаками при парной связи и между результа­тивным и множеством факторных признаков при многофакторной связи).

Регрессионный анализ – раздел математической статистики, изучает форму связи между признаками.

Различают следующие типы зависимостей между явлениями и их при­знаками:

1. Функциональная зависимость – связь, при которой каждому значению независимой переменной X соответствует точно определенное значениезависимой переменной Y (зависимость выработки продукции на одного рабочего от объема выпущенной продукции и численности рабочих).

2. Статистическая зависимость – связь, при которой каждому значению независимой переменной X соответствует множество значений зависимой перемен­ной Y и изменение которой происходит в условиях неопределенности, имеющей, как правило, случайный характер (зависимость всхожести семян некоторых культур от количества микроэлементов при их обработке, зависимость производительности труда на предприятии от его энерговооруженности и т. д.).

3. Корреляционная зависимость – частный случай статистический зависимости – связь, при которой каждому значению не­зависимой переменной X соответствует определенное математическое ожидание (среднее значение) зависимой переменной Y.

Условным математическим ожиданием M_x(Y)= 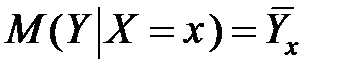(условной средней) называется математическое ожидание СВ Y, вычисленное в предположении, что СВ X приняла значение x.

Корреляционная зависимость бывает

1. Парная – связь между двумя признака­ми (результатив­ным Y и фактор­ным X или двумя факторными).

2. Частная – зависимость между ре­зультативным и одним факторным признаком или двумя фактор­ными признаками при фиксированных значе­ниях других факторных признаков.

3. Множественная – зависимость меж­ду результатив­ным признаком и двумя и более факторными при­знаками, вклю­ченными в иссле­дование.

Теснота связи количественно выражается величиной коэффициента корреляции.

Связи, в зависимости от количества признаков, включенных в модель подразделяются на

1.Однофакторные – связь между одним приз­наком-фактором и результативным признаком (при абстрагировании от влияния других).

2.Многофакторные – связь между несколькими факторными признаками и результативным признаком (факторы действуют комплек­сно, т.е. одновременно и во взаимосвязи).

Корреляционная зависимость исследуется с помощью мето­дов корреляционного и регрессионного анализа.

Линейная парная регрессия

По выборке ограниченного объема можно искать регрессионную зависимость в определенном виде, например, в виде линейной зависимости:

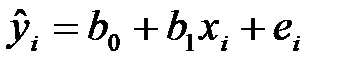(эмпирическое линейное уравнение регрессии),

(1)

где 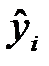– оценка условного математического ожидания 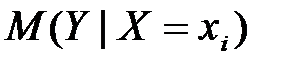; 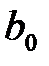и 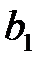– оценки неизвестных параметров, называемые эмпирическими коэффициентами линейной регрессии, отклонение 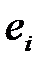– оценка теоретического случайного откло­нения .

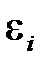Модель линейной регрессии (линейное уравнение) является наиболее распространенным (и простым) видом зави­симости между экономическими переменными. Кроме того, по­строенное линейное уравнение может служить начальным этапом эконометрического анализа.

Задачи линейного регрессионного анализа (см. Пример 2):

1. По имеющимся статистическим данным 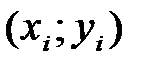, 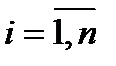получить наилучшие оценки неизвестных параметров;

2. Проверить статистические гипотезы о параметрах модели;

3. Проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным на­блюдений).

Метод наименьших квадратов

Различные выборки из одной и той же генеральной совокупности обычно приводят к определению отличающихся друг от друга оценок. Требуется по конкретной выборке 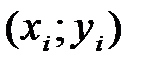, , 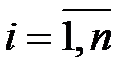найти оценк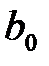и и 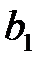неизвестных параметров уравнения (1) так, чтобы соответствующая линия регрессии (прямая) являлась бы наилучшей в определенном смысле среди всех других прямых. Другими словами, построенная прямая должна быть «ближайшей» к точкам наблюдений по их совокупности. Мерами качества найденных оценок могут служить опреде­ленные функции отклонений (невязок) , .

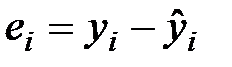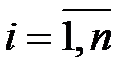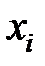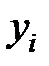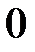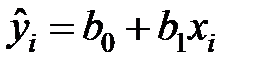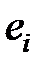Рис. 1

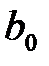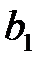Самым распространенным является метод наименьших квадратов (МНК)нахождения коэффициентов (оценок) и уравнения эмпирической линейной регрессии. Согласно МНК эти коэффициенты выбираются таким образом, чтобы минимизировать функцию (сумму квадратов отклонений):

.

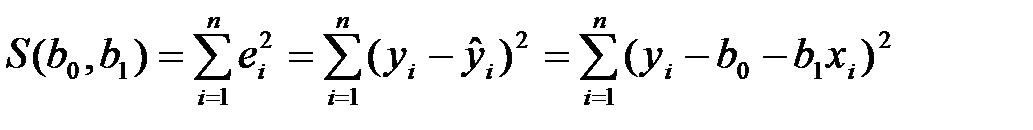Необходимым условием минимума данной функции является равенство нулю ее частных производных по параметрам 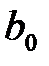и 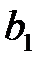, откуда для определения параметров линейной регрессии получаем линейную систему алгебраических уравнений:

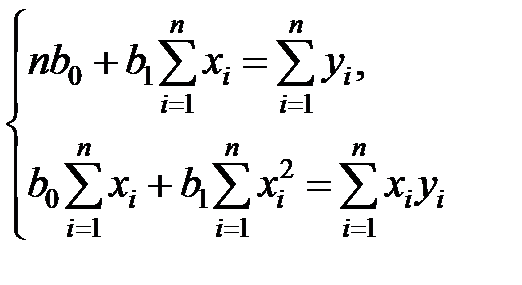
Коэффициент 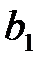называется выборочным коэффициентом регрессии Y на X. Он показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной X на одну единицу.

Коэффициент 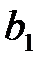нельзя непосредственно использовать для оценки влияния факторного признака x на результативный признак y из-за различия единиц измерения исследуемых показателей. Для этих целей применяется коэффициент эластичности

,

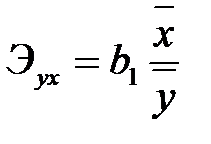где 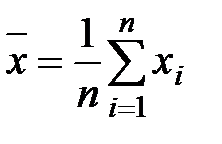, 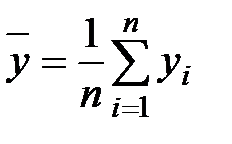– средние значения независимой и зависимой переменной.

Коэффициент эластичности показывает, на сколько процентов изменяется результативный признак y при изменении факторного признака x на один процент.

Основные положения регрессионного анализа. Теорема Гаусса-Маркова. Оценки параметров регрессионной модели и их свойства

МНК обеспечивает оптимальные свойства оценкам лишь при выполнении следующих основных предпосылок регрессионного анализа:

1. Математическое ожидание случайного отклонения 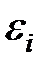равно 0: 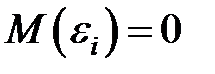для всех наблюдений, т.е. случайное отклонение в среднем не оказывает влияния на зависимую переменную.

2. Дисперсия случайного отклонения постоянна для любого : 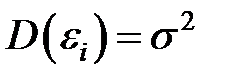(условие гомоскедастичности — постоянства дисперсий).

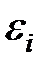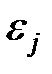3. Случайные отклонения и являются независимыми друг от друга, если 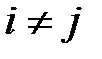. Если это условие выполняется, то говорят об отсутствии автокорреляции. С учетом выполнения условия 1 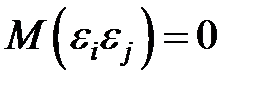, если .

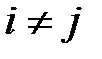4. Случайное отклонение независимо от объясняющих переменных. Обычно это условие выполняется автоматически, если объясняющая переменная 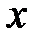не является случайной в данной модели.

5. Случайное отклонение 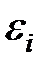есть нормально распределенная случайная величина.

Теорема Гаусса-Маркова. Если регрессионная модель удовлетворяет предпосылкам 1—4, то оценк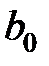и и 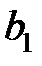имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.

Таким образом, оценк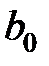и и 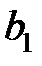полученные по методу МНК являются:

Ø несмещенными, так как 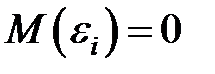, что говорит об отсутствии систематической ошибки в определении положения линии регрессии,

Ø состоятельными, так как дисперсия оценок параметров при возрастании числа 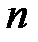наблюдений стремится к нулю (при увеличении объема выборки надежность оценок увеличивается),

Ø эффективными, т.е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров, линейными относительно величин .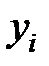

Требование выполнения предпосылки 5 необходимо для оценки точности уравнения регрессии и его параметров.

Для проверки гипотезы о статистической значимости коэффициента регрессии, т.е. гипотезы 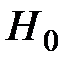: 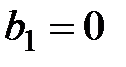, при конкурирующей (альтернативной) гипотезе 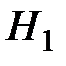: 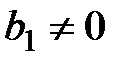, используется t-статистика:

,

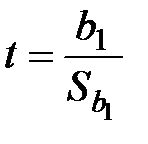которая при выполнении исходных предпосылок модели, имеет распределение Стьюдента с числом степеней свободы 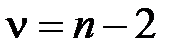, где 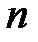– число наблюдений.

Гипотеза 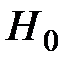отклоняется, если 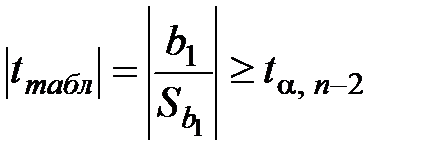, где 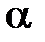– требуемый уровень значимости, в противном случае – принимается.

Если гипотеза 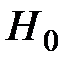принимается, что дает (эмпирическое) основание полагать, что ве­личина Y не зависит от X. В этом случае говорят, что коэффи­циент 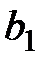статистически незначим. При отклонении 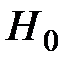коэффициент 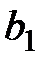считается статистически значимым, что дает (эмпирическое) основание наличия определенной линейной зависимости между Y и X.

По аналогичной схеме на основе t-статистики проверяется гипотеза о статистической значимости коэффициента :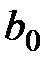

.

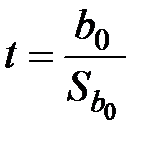Для парной регрессии более важным является анализ статистической значимости коэффициента 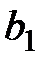, так как именно он позволяет оценить влияние объясняющей переменной X на зависимую переменную Y.

Пример 2.Для данных их примера 1: оценить тесноту и направление связи между переменными с помощью коэффициента корреляции; оценить значимость полученного коэффициента корреляции по критерию Стьюдента (уровень значимости 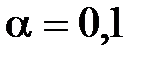); найти уравнение регрессии У по X. Сделать выводы.

Решение. Будем искать уравнение регрессии в виде 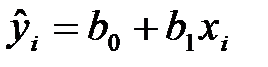, 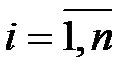. Оценим тесноту и направление связи между переменными с помощью коэффициента корреляции 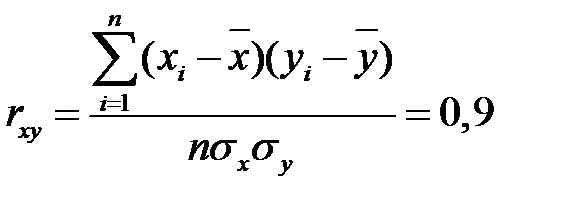. Поскольку коэффициент корреляции положительный, связь прямая. Коэффициент корреляции близок к единице, связь сильная.

Для проверки значимости коэффициента корреляции используется t-критерий Стьюдента

.

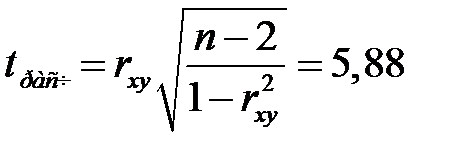При уровне значимости 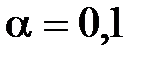и, учитывая, что в нашем примере количество степеней свободы равно 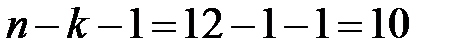, 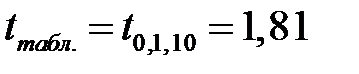. Так как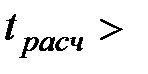 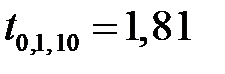, то значение коэффициента корреляции признается значимым. Парный коэффициент детерминации: 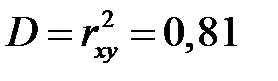. Это значит, что изменение y на 81% зависит от изменения исследуемых факторов, а на долю других факторов приходится 19% изменения результативного показателя.

Найдем уравнение регрессии Y по X. Вычисления по МНК удобно выполнять, используя следующую табл. 3.

Таблица 3

i	xi	yi	xixi	xiyi
сумма
среднее	32,42	24,42

Согласно МНК, имеем

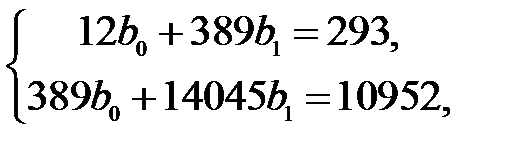
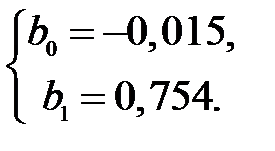
Таким образом, эмпирическое уравнение парной линейной регрессии имеет вид

.

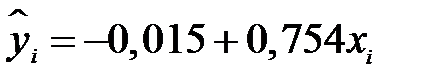Изобразим данную прямую на корреля­ционном поле. Построим эту прямую, например, по следующим двум точкам 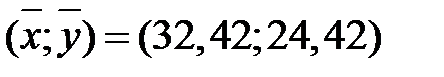и .

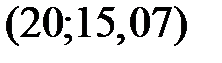Коэффициент 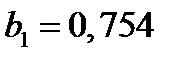показывает, на какую величину изменятся инвестиции в данное предприятие, если объем производства этого предприятия возрастает на одну единицу.

Воздействие неучтенных факторов и ошибок наблюдений определяется с помощью дисперсии случайных отклонений 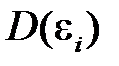. Несмещенной оценкой этой дисперсии является выборочная остаточная дисперсия.

Прогнозируемое значении переменнойy вычисляется по формуле

.

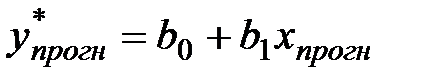Данный прогноз является точечным.

Решение.

На плоскости переменных и 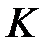построим точки 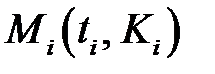и соединим их плавной кривой (рис. 15).

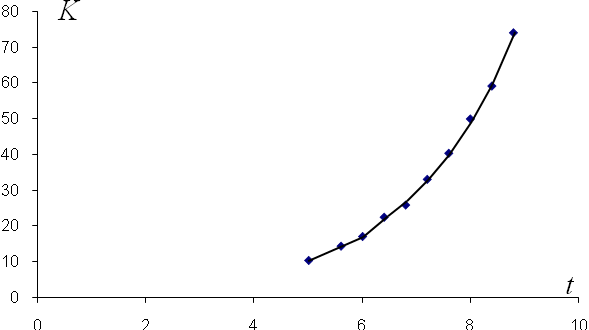
Рис. 15. Диаграмма исходных данных

По виду полученной диаграммы предполагаем, что для данного случая можно использовать зависимост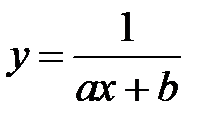и или .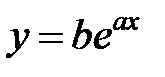

Рассмотрим зависимость

.

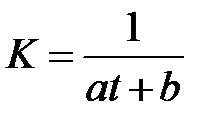Используя преобразование

,

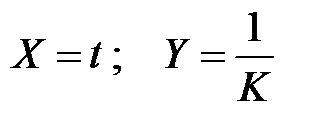зависимость 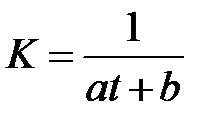преобразуем в линейную 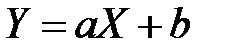. Найдем значения новых переменных X и Y и результаты расчетов занесем в табл. 5.

Таблица 5

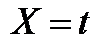	5,0	5,6	6,0	6,4	6,8	7,2	7,6	8,0	8,4	8,8
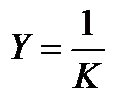	0,096	0,069	0,058	0,044	0,039	0,030	0,024	0,020	0,016	0,013

Построив на плоскости OXY точки 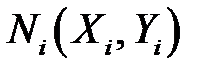, 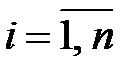(рис. 16), мы видим, что они расположены вдоль некоторой кривой, а не прямой линии.

Рис. 16.

Предположим теперь, что зависимость описывается формулой 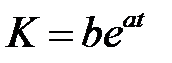. Используя преобразование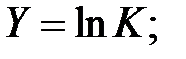 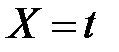, получим

.

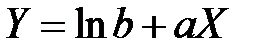Найдем значения новых переменных X и Y по формулам 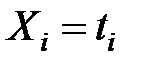; 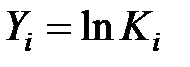и запишем в табл. 6

Таблица 6

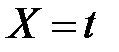	5,0	5,6	6,0	6,4	6,8	7,2	7,6	8,0	8,4	8,8
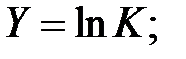	2,34	2,67	2,84	3,11	3,25	3,50	3,70	3,91	4,08	4,31

На плоскости XOY построим точки 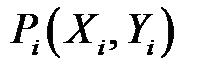, 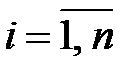. Как видно на (рис. 17), они расположены вдоль некоторой прямой линии, следовательно, выбранная зависимость лучше соответствует исходным данным.

Рис. 17.

Параметры 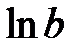и 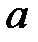найдем МНК. Для вычисления коэффициентов системы составим табл. 7.

Таблица 7

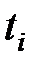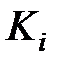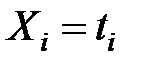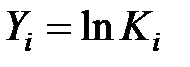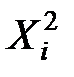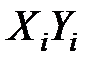	10,4		2,3418		11,709
5,6	14,4	5,6	2,6672	31,36	14,936
	17,1		2,8391		17,034
6,4	22,5	6,4	3,1135	40,96	19,926
6,8	25,9	6,8	3,2542	46,24	22,129
7,2	33,1	7,2	3,4995	51,84	25,197
7,6	40,4	7,6	3,6988	57,76	28,111
			3,912		31,296
8,4	59,2	8,4	4,0809	70,56	34,28
8,8	74,1	8,8	4,3054	77,44	37,888
	∑	69,8	33,713	501,16	242,51

Составим нормальную систему уравнений

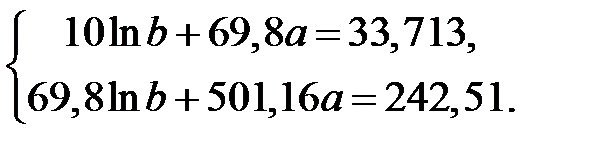
Решая ее, находим 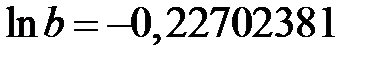и 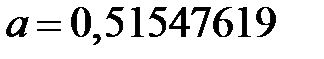. Отсюда получаем значение параметра 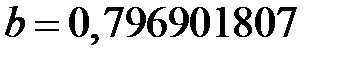. Таким образом, исходную зависимость можно описать функцией .

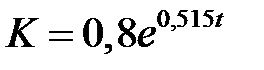Мультиколлинеарность

Если в модель включаются два или более тесно взаимосвязанных фактора, то наряду с уравнением регрессии появляется и другая зависимость. Мультиколлинеарность — тесная зависимость между факторными признаками, включенными в модель. Онаискажает величину коэффициентов регрессии и затрудняет их экономическую интерпретацию. Мультиколлинеарность возникает лишь в слу­чае множественной регрессии.

В решении проблемы мультиколлинеарности можно выде­лить несколько этапов.

1. Установление наличия мульти­коллинеарности.

2. Определение причин возник­новения мульти­коллинеарности.

3. Разработка мер по устранению мультиколлинеар­ности.

Способы определения наличия мультиколлинеарности:

1. Анализ матрицы коэффициентов парной корреляции.Факторы х_i и х_j могут быть признаны коллинеарными, если r_xixj > 0,8.

2. Исследование матрицы X’X. Если определитель матрицы X’X близок к нулю, то это свидетельствует о наличии мультиколлинеарности.

3. Коэффициент детерминации R² достаточно высок, но не­которые из коэффициентов регрессии статистически незначи­мы, т.е. они имеют низкие t-статистики.

Выделяют следующие методы устранения или уменьшения мультиколлинеарности:

1. Сравнение значений линейных коэффициентов корреляции; при отборе факторов предпочтение отдается тому фактору, который более тесно, чем другие факто­ры, связан с результативным признаком, причем желательно, чтобы связь данного факторного при­знака с у была выше, чем его связь с другим фак­торным признаком.

2. Метод включения факторов; в модель включают­ся факторы по одному в определенной последова­тельности, после включения каждого фактора в модель рас­считывают ее характеристики и модель проверяют на достоверность.

3. Метод исключения факторов; в модель включаются все факторы, после построения уравнения ре­грессии из модели исключают фактор, коэффици­ент при котором незначим и имеет наименьшее значение t-критерия. Процесс исключения факторов продолжается до тех пор, пока все коэффициенты ре­грессии не будут значимы.

4. Получение дополнительных данных или новой выборки.

5. Изменение спецификации модели.

6. Использование предварительной информации о некоторых параметрах.

Автокорреляция

Автокорреляция (последовательная корреляция) опреде­ляется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные данные).

Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов.

Методы определения автокорреляции:

1. Графический метод. По оси абсцисс отклады­ваются либо время (момент) получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения (либо оценки отклонений). По графику предполагают, имеются ли определенные связи между отклонениями, т.е. автокорреляция. Отсутствие зависимости, скорее всего, свидетельствует об отсутствии автокорреляции. Можно также график дополнить графиком зависимости e_t от e_t-1.

2. Тест Дарбина-Уотсона.

Гетероскедастичность

Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений. Выполнимость данной предпосылки называется гомоскедастичностъю. Невыполнимость данной предпосылки называется гетероскедастичностъю(непостоянством дисперсий отклонений). Проблема гетероскедастичности характерна для перекрестных данных и довольно редко встречается при рассмотрении временных рядов. Не существует однозначного метода определения гетероскедастичности. Однако для проверки разработано много тестов и критериев. Наиболее популярные и наглядные: графический анализ отклонений, тест ранговой корреляции Спирмена, тест Парка, тест Глейзера, тест Голдфелда—Квандта.

Использование графического представления отклонений по­зволяет определиться с наличием гетероскедастичности. В этом случае по оси абсцисс откладываются значения объясняю­щей переменной X (либо линейной комбинации объясняющих переменных), а по оси ординат либо отклонения, либо их квадраты.

Если все отклонения находятся внутри полосы постоянной ширины, параллельной оси абсцисс, то это говорит о независимости дисперсий от значений переменной X и их постоянстве, т.е. в этом случае выполняются условия гомоскедастичности.

Если наблюдаются некоторые систематические изменения в соотношениях между значениями переменной X и квадратами отклонений (линейная, квадратичная, гиперболическая и др. зависимости), то такие ситуации отражают большую вероятность наличия гетероскедастичности для рассматриваемых статистических данных.

Временные ряды

Для характеристики и анализа различных социально-экономи­ческих явлений за определенный период применяют показатели и методы, характеризующие эти процессы во времени (динамике). Под временным рядомв экономике понимается последовательность наблю­дений некоторого признака (случайной величины) Y в последовательные моменты времени. Отдельные наблюдения называются уровнями ряда, которые будем обозначать у_t (t= 1,2,..., n), где п – число уровней. Последовательно расположенные во времени числовые показатели характеризуют уровень состояния и изменения явления или процесса.

Классификация временных рядов:

1. В зависимости от показателя времени, временные ряды бывают моментные (на определенную дату) и интервальные (за определенный период).

2. По форме представления уровни во временном ряду могут быть представлены абсолютными, средними и от­носительными величинами.

3. По расстоянию между уровнями временные ряды подразде­ляются на ряды с равноотстоящими и неравноотстоящими уровнями по времени. В равноотстоящих ря­дах даты регистрации периода следуют друг за другом с равными интервалами, в неравноотстоящихравные интервалы не соблю­даются.

4. По содержанию показатели временных рядов подразделяют на состоящие из частных показателей и агре­гированных показателей. Частные показатели характеризуют явления изолированно, односторонне (например, динамика показателей среднесуточного объема потребленной воды); агрегированные показатели являются производными от частных показателей и характеризуют изучаемое явление комплексно (например, динамика пока­зателей экономической конъюнктуры).

В общем виде при исследовании экономического временного ряда у_t выделяются несколько составляющих

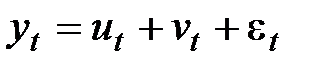
где 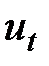— тренд, плавно меняющаяся компонента, описывающая чистое влияние долговременных факторов, т. е. длительную тенденцию изменения признака (например, рост населения, экономическое развитие, изменение структуры по­требления и т. п.);

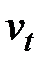, — сезонная компонента, отражающая повторяемость эконо­мических процессов в течение не очень длительного периода (года, иногда месяца, недели и т. д., например, объем продаж това­ров или перевозок пассажиров в различные времена года);

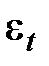— случайная компонента, отражающая влияние не поддаю­щихся учету и регистрации случайных факторов.

Следует обратить внимание на то, что в отличие от 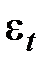первые составляющие 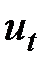, 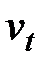являются закономерными, неслучайными.

Модели, в которых временной ряд представлен как сумма перечисленных компонент называются аддитивными; как произведение – мультипликативными моделями временного ряда.

1. Аддитивная модель имеет вид .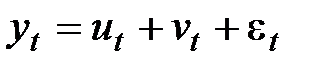

2. Мультипликативная модель 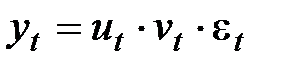. Такую модель применяют в случае, если про­исходят существенные сезонные изменения

Среди наиболее распространенных методов анализа времен­ных рядов выделим корреляционный анализ, модели авторегрессии и скользящей средней.

Важное значение в анализе временных рядов имеют стационарные временные ряды, вероятностные свойства которых не изменяются во времени. Стационарные временные ряды применяются, в частности, при описании случайных составляющих анализируемых рядов. Временной ряд 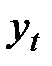(t= 1,2,..., n) называется стационарным, если совместное распределение вероятностей п наблюдений 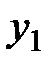, ,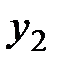..., 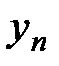такое же, как и п наблюдений 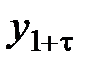, ,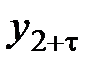..., 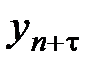при любых 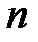, 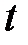и 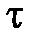. Иначе говоря, свойства стационарных рядов 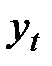не зави­сят от момента 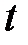, т. е. закон распределения и его числовые ха­рактеристики не зависят от 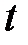. Поэтому математическое ожидание и среднее квадратическое отклонение могут быть оценены по наблюдениям 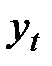(t= 1,2,..., n) по формулам

, .

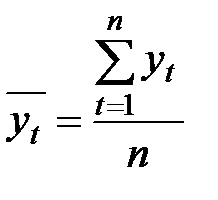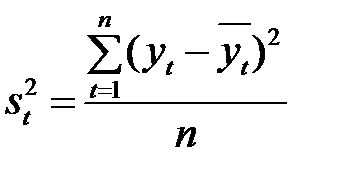Степень тесноты связи между последовательностями наблю­дений временного ряда 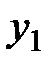, ,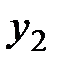..., 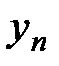и 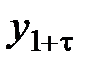, ,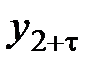..., 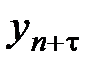(сдвинутых относительно друг друга на 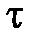единиц, или, как говорят, с лагом 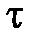) может быть определена с помощью коэффициента корреляции

,

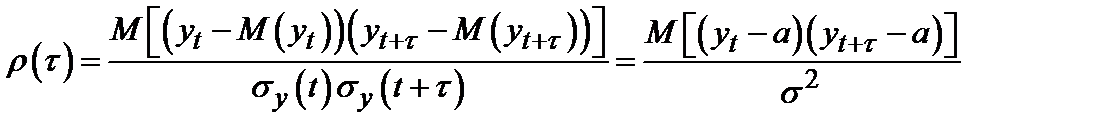ибо , .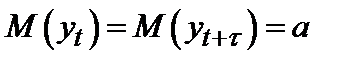

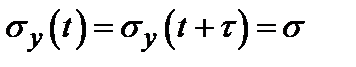Так как коэффициент 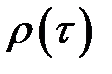измеряет корреляцию между членами одного и того же ряда, его называют коэффициентом автокорреляции, а зависимость 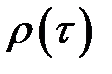– автокорреляционной функцией. В силу стационарности временного ряда 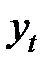, ( 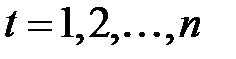) автокорреляционная функция 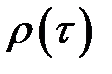зависит только от лага 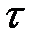, причем .

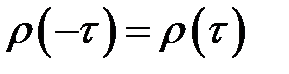Статистической оценкой 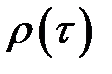является выборочный коэффициент автокорреляции 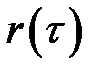, определяемый по формуле коэффициента корреляции:

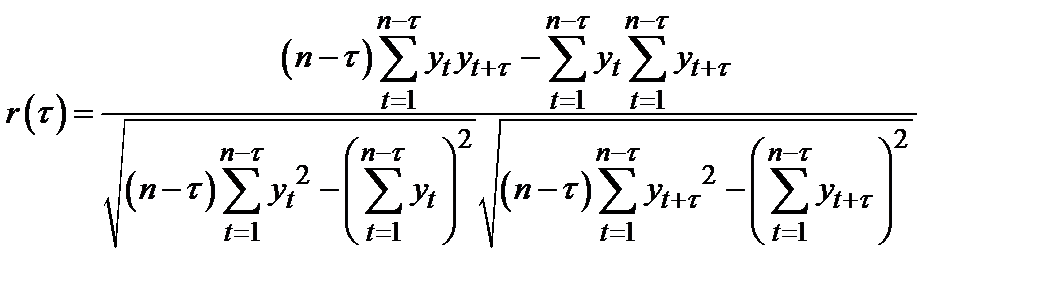
Функцию 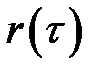называют выборочной автокорреляционной функцией, а ее график – коррелограммой. При расчете 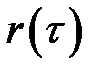следует помнить, что с увеличением 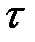число 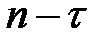пар наблюдений 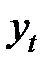, 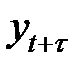уменьшается, поэтому лаг 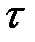должен быть таким, чтобы число 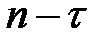было достаточным для определения 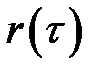. Обычно ориентируются на соотношение .

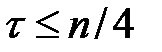Теоретический минимум

Основные понятия эконометрики

Эконометрика – наука, объединяющая совокупность математико-статистических методов моделирования и количественного анализа экономических явлений и процессов.

Эконометрика позволяет найти количественное подтверждение (либо не подтверждение) того или иного экономического закона или гипотезы. Одним из важнейших направлени