Основное уравнение динамики для вращательного движения.

Гипотезы и допущения

Расчет реальных конструкций и их элементов является либо теоретически невозможным, либо практически неприемлемым по своей сложности. Поэтому в сопротивлении материалов применяется модель идеализированного деформируемого тела, включающая следующие допущения и упрощения:

1. Гипотеза сплошности и однородности: материал представляет собой однородную сплошную среду; свойства материала во всех точках тела одинаковы и не зависят от размеров тела.

2. Гипотеза об изотропности

материала: физико-механические свойства материала одинаковы по всем направлениям.

3. Гипотеза об идеальной упругости материала: тело способно восстанавливать свою первоначальную форму и размеры после устранения причин, вызвавших его деформацию.

4. Гипотеза (допущение) о малости деформаций: деформации в точках тела считаются настолько малыми, что не оказывают существенного влияния на взаимное расположение нагрузок, приложенных к телу.

5. Допущение о справедливости закона Гука: перемещения точек конструкции в упругой стадии работы материала прямо пропорциональны силам, вызывающим эти перемещения.

6. Принцип независимости действия сил (принцип суперпозиции): результат воздействия нескольких внешних факторов равен сумме результатов воздействия каждого из них, прикладываемого в отдельности, и не зависит от последовательности их приложения.

7. Гипотеза Бернулли о плоских сечениях: поперечные сечения, плоские и нормальные к оси стержня до приложения к нему нагрузки, остаются плоскими и нормальными к его оси после деформации.

8. Принцип Сен-Венана: в сечениях, достаточно удалённых от мест приложения нагрузки, деформация тела не зависит от конкретного способа нагружения и определяется только статическим эквивалентом нагрузки.

Эти положения ограниченно применимы к решению конкретных задач. Например, для решения задач устойчивости утверждения 4-6 не справедливы, утверждение 3 справедливо не всегда.

32. Метод сечений

Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки. Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить.

33. Напряжение полное,нормальное,касательное

Метод сечений позволяет выявить внутренние силовые факторы. Но для оценки прочности необходимо уметь определять внутренние силы в любой точке сечения рассматриваемого бруса. Поэтому введем числовую меру интенсивности внутренних сил - напряжение.

Рассмотрим брус, к которому приложена некоторая нагрузка. Брус под действием нагрузки находится в равновесии. Применяя метод сечений, рассечем брус поперечной плоскостью, отбросим левую часть бруса, заменим действие отброшенной части на рассматриваемую системой внутренних сил. Выделим вокруг произвольной точки малую площадку 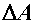(рис. а). Равнодействующую внутренних сил в пределах этой площадки обозначим .

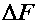Отношение 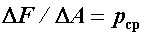называется средним напряжением. Вектор среднего напряжения совпадает по направлению с вектором равнодействующей .

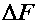При постепенном уменьшении площадки 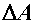изменяются как модуль, так и направление равнодействующей внутренних сил 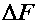, а следовательно, вектор 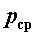постепенно приближается к истинному значению напряжения 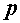в заданной точке (рис. б). Числовое значение этого напряжения выражается равенством .

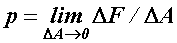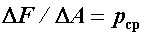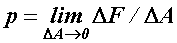Согласно формулам и , единицей напряжения служит единица силы, деленная на единицу площади. В Международной системе единиц (СИ) единица силы - Н, единица площади - 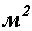, значит единица напряжения в этой системе - 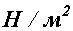названная паскалем, т.е. 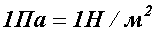. Паскаль - очень мелкая единица напряжения, поэтому более употребительной единицей является мегапаскаль: .

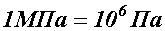Вектор 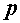полного напряжения в точке сечения можно разложить на два составляющих вектора: 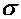и 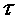(рис. а). Вектор 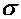, направленный перпендикулярно сечению, называется нормальным напряжением. Вектор 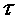, лежащий в плоскости сечения, называется касательным напряжением. Поскольку векторы 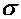и 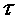взаимно перпендикулярны, зависимость между числовыми значениями напряжени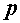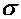й , и 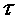выражается формулой .

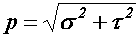Чаще оказывается целесообразным, сообразуясь с выбранными осями координат 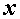, , 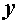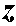(рис. б), разложить вектор 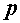не на две, а на три составляющие вектора: 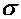(нормальное напряжение), параллельную ос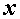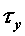и , и 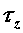(касательные напряжения), параллельные соответственно осям 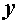и 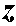. В этом случае .

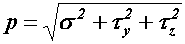Между внутренними силовыми факторами и напряжениям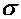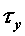и , и 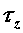существуют определенные зависимости, к установлению которых мы перейдем в следующих главах. Здесь жа заметим следующее.

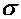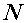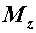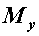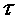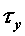Наличие нормального напряжения в любой точке поперечного сечения обусловлено возникновением в этом сечении нормальной силы или изгибающих моментов и . Наличие касательных напряжений или и 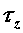обусловлено внутренними силовыми факторами, возникающими в плоскости сечения, т. е. поперечными силами 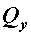, 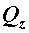или крутящим моментом .

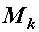34.Эпюра продольных сил

Если продольные силы, возникающие в различных поперечных сечениях стержня, неодинаковы, закон их изменения по длине стержня представляется в виде графика N(z), называемого эпюрой продольных сил. Эпюра продольных сил необходима для оценки прочности стержня и строится для того, чтобы найти опасное сечение (поперечное сечение, в котором продольная сила принимает наибольшее значение ).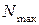

Из гипотезы плоских сечений следует: все продольные волокна стержня деформируются одинаково. Поэтому можно считать, что при растяжении (сжатии)напряжения во всех точках поперечного сечения стержня одинаковы и направлены по нормали к сечению. Такие напряжения, как уже отмечалось, называются нормальными напряжениями.

Из вышеизложенного вытекает формула нормальных напряжений при растяжении (сжатии):

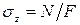
где N – продольное усилие, возникающее в данном поперечном сечении стержня, а F – площадь этого поперечного сечения.

Правило знаков для нормального напряжения ( 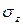), как и для продольной силы (N): при растяжении нормальное напряжение считается положительным, а при сжатии – отрицательным.

По определению относительная деформация стержня равна

,

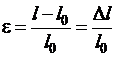где 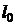, 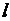– первоначальная и текущая длина стержня соответственно.

Если удлинение стержня 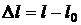вызвано действием растягивающих нормальных напряжений 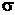, то относительная деформация

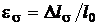
называется силовой деформацией (рис. 1.10, а). Если удлинение стержня вызвано изменением температуры 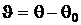, то деформация

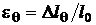
называется температурной деформацией (рис. 1.10, б).

Рис. 1.10. Силовая (а) и температурная (б) деформации

В общем случае удлинение стержня происходит за счёт действия приложенных нагрузок и изменения температуры. Поэтому

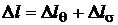
и

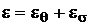. (1.16)

Как показывает опыт, силовая деформация стержня (рис. 1.10, а) пропорциональна действующим напряжениям 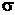, а температурная деформация стержня (рис. 1.10, б) пропорциональна приращению температуры :

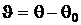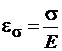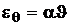, . (1.17)

Постоянная 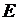называется модулем Юнга (модулем растяжения или модулем упругости первого рода), постоянная 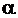– температурным коэффициентом линейного расширения. Для углеродистых сталей при комнатной температуре модуль Юнга и коэффициент линейного расширения имеют следующий порядок величины: 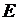» 2×1011 Па, 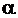» 12×10–6 К–1.

Подставляя (1.17) в (1.16), имеем

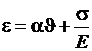(1.18)

или

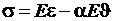. (1.19)

Равенство (1.19), как и эквивалентное ему равенство (1.18), носит название закона Гука при растяжении.

К примеру, если оба конца стержня закреплены, то его длина неизменна, а деформация 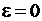. Тогда по формуле (1.16) при нагревании (охлаждении) стержня силовая деформация равна и противоположна по знаку тепловой деформации:

.

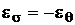Согласно (1.19) возникающие при этом напряжения равны

.

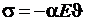Следовательно, когда приращение температуры 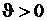, в стержне действуют сжимающие напряжения: 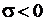. Напротив, в случае 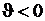в стержне возникают растягивающие напряжения: .

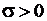Дополнение

35. ГУКА ЗАКОН - основной закон теории упругости, выражающий линейную зависимость между напряжениями и малыми деформациями в упругой среде. Установлен P. Гуком (R. Hooke) в 1660.

При растяжении стержня длиной l его удлинение 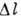пропорц. растягивающей силе F; в этом случае Г. з. имеет вид 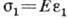, где 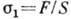- нормальное напряжение в поперечном сечении стержня, 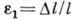- относит. удлинение, S - площадь поперечного сечения. Константа материала E наз. модулем Юнга. При этом относит. изменение поперечных размеров стержня 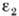пропорц. относительному удлинению: 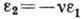. Константа 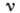наз. коэф. Пуассона