Графическое представление выборки. Полигон частот, гистограмма, эмпирическая функция распределения
Рисунки и графики представляют собой удобный и наглядный способ представления выборки. Выборку, извлеченную из дискретной генеральной совокупности, можно представить в виде полигона частот или полигона относительных частот. На плоскости в прямоугольной системе координат строят точки с координатами 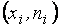 или
или 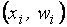 соответственно и соединяют эти точки отрезками прямых. Полученная ломаная и называется полигоном частот (если по оси ординат отложены частоты вариант) или полигоном относительных частот (если по оси ординат отложены относительные частоты вариант). Полигон можно построить и для сгруппированной выборки. Но чаще для отображения таких выборок используют гистограммы. Гистограмма – это столбчатая диаграмма, изображенная на координатной плоскости. Если отложить по оси абсцисс границы интервалов одинаковой ширины, на которые разбита сгруппированная выборка, а по оси ординат – частоты или относительные частоты соответствующих интервалов, то можно построить график в виде прямоугольников, ширина которых равна длине интервала, а высота – соответствующей частоте или относительной частоте. Полученная диаграмма называется гистограммой частот или гистограммой относительных частот соответственно. На гистограмме частот сумма всех высот равна
соответственно и соединяют эти точки отрезками прямых. Полученная ломаная и называется полигоном частот (если по оси ординат отложены частоты вариант) или полигоном относительных частот (если по оси ординат отложены относительные частоты вариант). Полигон можно построить и для сгруппированной выборки. Но чаще для отображения таких выборок используют гистограммы. Гистограмма – это столбчатая диаграмма, изображенная на координатной плоскости. Если отложить по оси абсцисс границы интервалов одинаковой ширины, на которые разбита сгруппированная выборка, а по оси ординат – частоты или относительные частоты соответствующих интервалов, то можно построить график в виде прямоугольников, ширина которых равна длине интервала, а высота – соответствующей частоте или относительной частоте. Полученная диаграмма называется гистограммой частот или гистограммой относительных частот соответственно. На гистограмме частот сумма всех высот равна 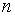 , а на гистограмме относительных частот – единице. Необходимо подчеркнуть, что гистограммы частот и относительных частот имеют смысл только в том случае, если все интервалы одинаковой ширины.
, а на гистограмме относительных частот – единице. Необходимо подчеркнуть, что гистограммы частот и относительных частот имеют смысл только в том случае, если все интервалы одинаковой ширины.
Существует также гистограмма статистического распределения. Для ее построения на оси ординат откладываются величины 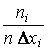 , где
, где 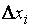 – ширина i-го интервала. Таким образом, высоты прямоугольников гистограммы статистического распределения пропорциональны частотам интервалов, а сумма их площадей
– ширина i-го интервала. Таким образом, высоты прямоугольников гистограммы статистического распределения пропорциональны частотам интервалов, а сумма их площадей
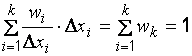 .
.
Гистограмму статистического распределения можно считать аналогом графика функции плотности вероятности 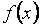 непрерывной случайной величины, площадь под графиком
непрерывной случайной величины, площадь под графиком 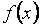 равна 1.
равна 1.
Эмпирическая функция распределения (функция распределения выборки) – это функция 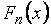 , определяющая для каждого значения
, определяющая для каждого значения 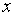 относительную частоту события
относительную частоту события 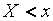 ,
,
 ,
,
где 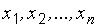 – члены вариационного ряда выборки.
– члены вариационного ряда выборки.
Функция распределения выборки – это статистический аналог графика функции распределения 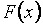 непрерывной случайной величины. Ее график представляет собой ступенчатую фигуру со скачками, кратными величине
непрерывной случайной величины. Ее график представляет собой ступенчатую фигуру со скачками, кратными величине 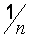 в точках, определяемых членами вариационного ряда. Как оценка
в точках, определяемых членами вариационного ряда. Как оценка 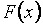 функция
функция 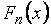 случайна. Согласно теореме Гливенко, при стремлении числа испытаний к бесконечности вероятность того, что эмпирическая функция распределения выборки отклонится от теоретической функции распределения генеральной совокупности на малую положительную величину
случайна. Согласно теореме Гливенко, при стремлении числа испытаний к бесконечности вероятность того, что эмпирическая функция распределения выборки отклонится от теоретической функции распределения генеральной совокупности на малую положительную величину 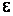 , равна 1:
, равна 1:
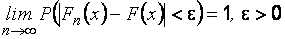 .
.
Иными словами, с увеличением числа опытов эмпирическая функция распределения все лучше описывает закон распределения генеральной совокупности, из которой взята выборка.
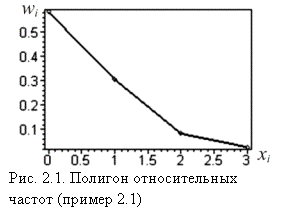 | Основные свойства функции распределения выборки. 1. Эмпирическая функция распределения принимает значения из интервала 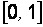 ( ( 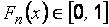 ). 2. Функция распределения выборки является неубывающей, непрерывной слева функцией. 3. Если ). 2. Функция распределения выборки является неубывающей, непрерывной слева функцией. 3. Если 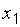 – наименьшее опытное значение, то для – наименьшее опытное значение, то для  . Если . Если 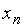 – наибольшая варианта, то для – наибольшая варианта, то для 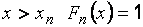 . На рис. 2.1–2.3 показаны полигон относительных частот для выборки примера 2.1, гистограмма и эмпирическая функция распределения для выборки примера 2.2 соответственно. . На рис. 2.1–2.3 показаны полигон относительных частот для выборки примера 2.1, гистограмма и эмпирическая функция распределения для выборки примера 2.2 соответственно. |
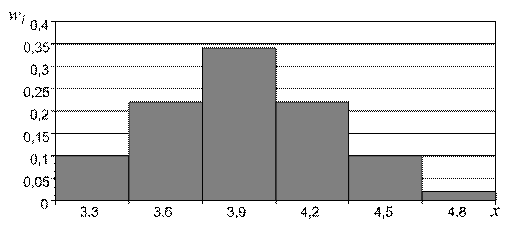
Рис. 2.2. Гистограмма относительных частот (пример 2.2)
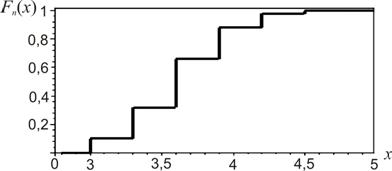
Рис. 2.3. Эмпирическая функция распределения (пример 2.2)
Оценка параметров генеральной совокупности. Ошибка репрезентативности. Требования к статистической оценке. Доверительная вероятность, предельная и средняя квадратическая ошибка выборки при оценке генеральной средней и генеральной доли. Необходимый объем выборки для обеспечения доверительной вероятности.
Основными параметрами генеральной совокупности являются математическое ожидание (генеральная средняя) М(Х) и среднее квадратическое отклонение s. Это постоянные величины, которые можно оценить по выборочным данным. Оценка генерального параметра, выражаемая одним числом, называется точечной.
Точечной оценкой генеральной средней является выборочное среднее 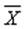 .
.
Выборочным средним называется среднее арифметическое значение признака выборочной совокупности.
Если все значения x1, x2,..., xn признака выборки различны (или если данные не сгруппированы), то:
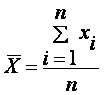
Если же все значения признака x1, x2,..., xn имеют соответственно частоты n1, n2,..., nk, причем n1 + n2 +...+ nk = n (или если выборочное среднее вычисляется по вариационному ряду), то
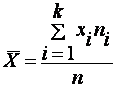
В том случае, когда статистические данные представлены в виде интервального вариационного ряда, при вычислении выборочного среднего 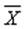 значениями вариант считают середины интервалов.
значениями вариант считают середины интервалов.
Выборочное среднее является основной характеристикой положения, показывает центр распределения совокупности, позволяет охарактеризовать исследуемую совокупность одним числом, проследить тенденцию развития, сравнить различные совокупности (выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0).
Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и стандартного отклонения.
Дисперсия выборки или выборочная дисперсия (от английского variance) – это мера изменчивости переменной. Термин впервые введен Фишером в 1918 году.
Выборочной дисперсией Dв называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения 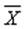 .
.
Если все значения x1, x2,..., xn признака выборки объема n различны, то:
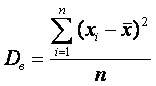
Если же все значения признака x1, x2,..., xn имеют соответственно частоты n1, n2,..., nk, причем n1 + n2 +...+ nk = n, то
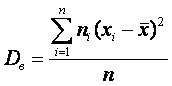
Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны.
Среднее квадратическое отклонение (стандартное отклонение), (от английского standarddeviation) вычисляется как корень квадратный из дисперсии.

Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего.
Непараметрическими характеристиками положения являются мода и медиана.
Модой Mo называется варианта, имеющая наибольшую частоту или относительную частоту.
Медианой Me называется варианта, которая делит вариационный ряд на две части, равные по числу вариант.
При нечетном числе вариант (n=2k+1)
Me = xk+1,
а при четном числе вариант (n=2k)
Me = (xk + xk+1)/2.
Ошибки репрезентативности характерны только для выборочного наблюдения и возникают в результате того, что выборочная совокупность не полностью воспроизводит генеральную. Они определяются как расхождение между значениями показателей, полученных по выборке, и значениями показателей этих же величин, которые были бы получены при проведенном сплошном наблюдении с одинаковой степенью точности
Расчет ошибки репрезентативности (mм) средней арифметической величины (М):

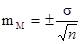 , где σ - среднее квадратическое отклонение; n - численность выборки (>30).
, где σ - среднее квадратическое отклонение; n - численность выборки (>30).
Расчет ошибки репрезентативности (mР) относительной величины (Р):
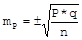 , где Р - соответствующая относительная величина (рассчитанная, например, в %);
, где Р - соответствующая относительная величина (рассчитанная, например, в %);
Q =100 - Ρ% - величина, обратная Р; n - численность выборки (n>30)
В клинических и экспериментальных работах довольно часто приходится использовать Малую выборку, Когда число наблюдений меньше или равно 30. При малой выборке для расчета ошибок репрезентативности, как средних, так и относительных величин, Число наблюдений уменьшается на единицу, т. е.
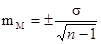 ;
; 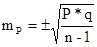 .
.
Величина ошибки репрезентативности зависит от объема выборки: чем больше число наблюдений, тем меньше ошибка. Для оценки достоверности выборочного показателя принят следующий подход: показатель (или средняя величина) должен в 3 раза превышать свою ошибку, в этом случае он считается достоверным.
Знание величины ошибки недостаточно для того, чтобы быть уверенным в результатах выборочного исследования, так как конкретная ошибка выборочного исследования может быть значительно больше (или меньше) величины средней ошибки репрезентативности. Для определения точности, с которой исследователь желает получить результат, в статистике используется такое понятие, как вероятность безошибочного прогноза, которая является характеристикой надежности результатов выборочных медико-биологических статистических исследований. Обычно, при проведении медико-биологических статистических исследований используют вероятность безошибочного прогноза 95% или 99%. В наиболее ответственных случаях, когда необходимо сделать особенно важные выводы в теоретическом или практическом отношении, используют вероятность безошибочного прогноза 99,7%
