Операции над событиями. Сложение и умножение событий и их вероятностей.

Определения:

· Под суммой нескольких событий понимается событие, состоящее в том, что хотя бы одно из суммируемых событий произойдет.

· Под произведением нескольких событий понимается событие, состоящее в совместном наступлении всех событий.

Теорема сложения вероятностей несовместных событий:

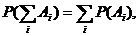
Следствия:

· Для полной системы событий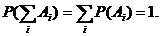

· Вероятность противоположного события: P( 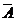)= 1-Р(А).

Теорема сложения вероятностей двух совместных событий:

P(A+B)=P(A)+P(B)-P(AB).

Теорема умножения вероятностей:

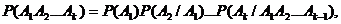
где события Аi( 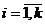) - могут быть, в общем случае, зависимыми; 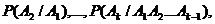- условные вероятности событий.

Теорема умножения вероятностей независимых событий:

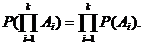
Пример 2.1. Два стрелка по очереди стреляют в мишень. Если не попадет один, то начинает стрелять другой. Найти вероятность того, что после трех выстрелов в мишени будет две пробоины; если вероятность попадания в мишень для первого стрелка, начинающего стрельбу - 0.7, для второго - 0.8.

Решение.Аi- событие, состоящее в том, что первый стрелок при i-ом выстреле попадет, а 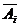- не попадет в цель. Вi - событие состоящее в том, что . второй стрелок при i-том выстреле попадет, а 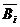- не попадет в цель.

P(Аi)=0,7; P(Вi)=0,8; P( 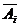)= 1-0,7 = 0,3; Р( 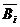) = 1-0,8 = 0,2.

Все события Аi , 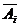, Вi , 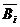- независимы друг от друга. С- событие, состоящее в том, что после трех выстрелов в мишени будет две пробоины. 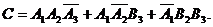С помощью теоремы сложения вероятностей несовместных событий и теоремы умножения вероятностей для независимых событий можно найти вероятность данного события.

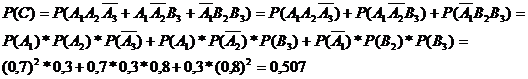
Пример 2.2. На рынке ценных бумаг предлагались к продаже пакеты акций пяти различных предприятий. Господин «N» приобрел три пакета акций различных предприятий. Два предприятия отказались выплачивать дивиденды по итогам текущего года. Найти вероятность того, что не менее двух пакетов акций принесли дивиденды данному господину.

Решение. Предположим, что господин выбирал пакеты акций случайным образом. Для каждого i-того выбранного пакета может наступить одно из событий: не будут выплачены дивиденды 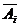или будут - Аi. События Аi, 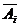- зависимы друг от друга.

Рассмотрим событиеВ, состоящее в том, что не менее двух пакетов акций из трех (т.е. или два или три) принесут дивиденды данному господину.

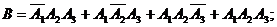
По теореме сложения вероятностей несовместных событий:

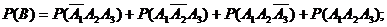
По теореме умножения вероятностей для зависимых событий и классической.формулы вероятности события можно найти вероятность данного события.

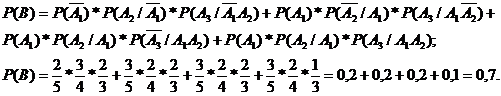
Пример 2.3. В магазин поступили соответственно 20, 15, и 10 пальто трех различных фирм, Известно, что доля высококачественных изделий среди продукции первой фирмы в среднем составляет 70%, второй -80%, третьей - 60%. Наудачу выбранное пальто оказалось плохим. Найти вероятность того, что оно поставлено второй фирмой.

Решение. Для выбранного пальто могут наступить события: Hi - оно поставлено i-той фирмой, A - оно оказалось плохим. Группа событий: 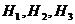- является полной, причем событие Aможет появиться только вместе с одним из них. По условию задачи:

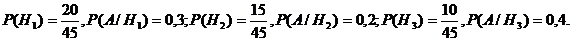
Полная вероятность событияА:

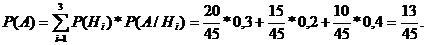
Выбранное пальто оказалось плохим, наступило событие А. Определим вероятность «гипотезы, состоящей в том, что пальто поставлено в магазин второй фирмой» по формуле Байеса:

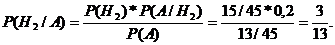
Пример 2.4. Имеются две урны. В первой – семь красных шаров и три черных, во второй – три красных и четыре черных. Из первой урны переложили во вторую один шар, затем, перемешав шары, из второй урны переложили в первую один шар. Найти вероятность того, что шар, извлеченный после этого из первой урны, окажется красным. Из первой урны после перекладывания шаров достали наугад красный шар. Какова вероятность того, что количество красных шаров в урне после перекладывания не изменилось?

Решение.Поскольку после перекладывания шаров мы достоверно не знаем сколько в урне находится красных, а сколько черных шаров, то можно выдвинуть гипотезы Hiотносительно количества красных и черных шаров в первой урне. Всего шаров как было, так и осталось 10, из них число красных могло уменьшиться на один (H1), остаться прежним (H2) или увеличиться на один шар (H3). СобытиеА – достать из первой урны красный шар. Группа событий: 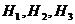- является полной, причем событие Aможет появиться только вместе с одним из них. Расчеты в данной задаче можно оформить в виде следующей таблицы:

i	Hi	P(Hi)	P(A/ Hi)	P(Hi)*P(A/ Hi)	P(Hi /A)
	6 кр, 4 ч.		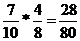0,6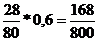
	7 кр, 3 ч.		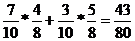0,7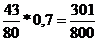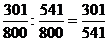
	8 кр, 2 ч.		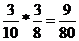0,8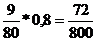
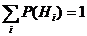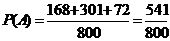