Методика проверки статистических гипотез

Статистические гипотезы

• Нулевая гипотеза (null hypothesis) – гипотеза об отсутствии различий (утверждение об

отсутствии различий в значениях или об отсутствии связи в генеральной совокупности)

• Согласно нулевой гипотезе (Н0), различие между значениями недостаточно значительно, а

независимая переменная не оказывает никакого влияния

Альтернативная гипотеза (alternative hypothesis) – гипотеза о значимости различий

(утверждает наличие различий или существование связи)

• Альтернативная гипотеза (HА) является «рабочей» гипотезой исследования. В

соответствии с этой гипотезой, различия достаточно значимы и обусловлены влиянием

независимой переменной

• Ненаправленная и направленная альтернативы

Н0: μ=50

НА: μ≠50

НА: μ>50

НА: μ<50

• Нулевая и альтернативная гипотезы представляют полную группу несовместных событий:

отклонение одной влечет принятие другой

• Основной принцип метода проверки гипотез состоит в том, что выдвигается нулевая

гипотеза Н0, с тем чтобы попытаться опровергнуть ее и тем самым подтвердить

альтернативную гипотезу HА. Если результаты статистического теста, используемого для

анализа разницы между средними, окажутся таковы, что позволят отклонить Н0, это будет

означать, что верна НА, т.е. выдвинутая рабочая гипотеза подтверждается

• Не можем отклонить нулевую гипотезу - не значит «принять» альтернативную

(нулевая гипотеза никогда не может быть абсолютно подтверждена!)

Пусть задана случайная выборка 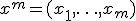— последовательность 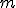объектов из множества 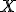. Предполагается, что на множестве 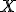существует некоторая неизвестная вероятностная мера .

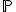Методика состоит в следующем.

1. Формулируется нулевая гипотеза 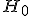о распределении вероятностей на множестве 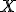. Гипотеза формулируется исходя из требований прикладной задачи. Чаще всего рассматриваются две гипотезы —основная или нулевая 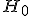и альтернативная 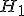. Иногда альтернатива не формулируется в явном виде; тогда предполагается, что 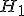означает «не 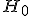». Иногда рассматривается сразу несколько альтернатив. В математической статистике хорошо изучено несколько десятков «наиболее часто встречающихся» типов гипотез, и известны ещё сотни специальных вариантов и разновидностей. Примеры приводятся ниже.

2. Задаётся некоторая статистика (функция выборки) 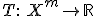, для которой в условиях справедливости гипотезы 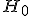выводится функция распределения 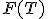и/или плотность распределения 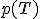. Вопрос о том, какую статистику надо взять для проверки той или иной гипотезы, часто не имеет однозначного ответа. Есть целый ряд требований, которым должна удовлетворять «хорошая» статистика 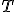. Вывод функции распределения 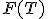при заданных 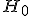и 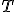является строгой математической задачей, которая решается методами теории вероятностей; в справочниках приводятся готовые формулы для 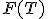; в статистических пакетах имеются готовые вычислительные процедуры.

3. Фиксируется уровень значимости — допустимая для данной задачи вероятность ошибки первого рода, то есть того, что гипотеза на самом деле верна, но будет отвергнута процедурой проверки. Это должно быть достаточно малое число 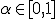. На практике часто полагают .

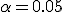4. На множестве допустимых значений статистики 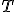выделяется критическое множество 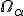наименее вероятных значений статистики 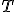, такое, что 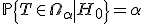. Вычисление границ критического множества как функции от уровня значимости 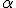является строгой математической задачей, которая в большинстве практических случаев имеет готовое простое решение.

5. Собственно статистический тест (статистический критерий) заключается в проверке условия:

§ если 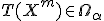, то делается вывод «данные противоречат нулевой гипотезе при уровне значимости 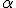». Гипотеза отвергается.

§ если 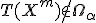, то делается вывод «данные не противоречат нулевой гипотезе при уровне значимости 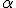». Гипотеза принимается.

Итак, статистический критерий определяется статистикой 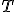и критическим множеством 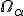, которое зависит от уровня значимости .

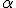Процедура проверки статистической гипотезы

• Сформулировать нулевую и альтернативной гипотезы

• Выбрать соответствующий статистический тест

• Выбрать требуемый уровень значимости (α=0.05, 0.01, 0.025, …)

• Вычислить эмпирическое значение критерия по тесту

• Сравнить с критическим значением критерия по тесту

• Принять решение (для большинства тестов приемлемо

правило: если вычисленное значение больше, чем критическое,

нулевая гипотеза отклоняется)

Критерий согласия Пирсона

Критерий согласия Пирсона (χ²) применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению F(x) при большом объеме выборки (n ≥ 100). Критерий применим для любых видов функции F(x), даже при неизвестных значениях их параметров, что обычно имеет место при анализе результатов механических испытаний. В этом заключается его универсальность.

Использование критерия χ² предусматривает разбиение размаха варьирования выборки на интервалы и определения числа наблюдений (частоты) n_j для каждого из e интервалов. Для удобства оценок параметров распределения интервалы выбирают одинаковой длины.

Число интервалов зависит от объема выборки. Обычно принимают: при n = 100 e = 10 ÷ 15, при n = 200 e = 15 ÷ 20, при n = 400 e = 25 ÷ 30, при n = 1000 e = 35 ÷ 40.

Интервалы, содержащие менее пяти наблюдений, объединяют с соседними. Однако, если число таких интервалов составляет менее 20 % от их общего количества, допускаются интервалы с частотой n_j ≥ 2.

Статистикой критерия Пирсона служит величина
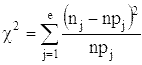, (3.91)
где p_j - вероятность попадания изучаемой случайной величины в j-и интервал, вычисляемая в соответствии с гипотетическим законом распределением F(x). При вычислении вероятности p_j нужно иметь в виду, что левая граница первого интервала и правая последнего должны совпадать с границами области возможных значений случайной величины. Например, при нормальном распределении первый интервал простирается до -∞, а последний - до +∞.

Нулевую гипотезу о соответствии выборочного распределения теоретическому закону F(x) проверяют путем сравнения вычисленной по формуле (3.91) величины с критическим значением χ²_α, найденным по табл. VI приложения для уровня значимости α и числа степеней свободы k = e₁ - m - 1. Здесь e₁ - число интервалов после объединения; m - число параметров, оцениваемых по рассматриваемой выборке. Если выполняется неравенство
χ² ≤ χ²_α (3.92)
то нулевую гипотезу не отвергают. При несоблюдении указанного неравенства принимают альтернативную гипотезу о принадлежности выборки неизвестному распределению.

Недостатком критерия согласия Пирсона является потеря части первоначальной информации, связанная с необходимостью группировки результатов наблюдений в интервалы и объединения отдельных интервалов с малым числом наблюдений. В связи с этим рекомендуется дополнять проверку соответствия распределений по критерию χ² другими критериями. Особенно это необходимо при сравнительно малом объеме выборки (n ≈ 100).

Критерий согласия Пирсона 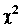– один из основных:

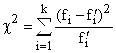
где k – число групп, на которые разбито эмпирическое распределение,
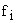– наблюдаемая частота признака в i-й группе,
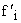– теоретическая частота.