Вероятность появления хотя бы одного события.
Тогда получим
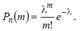 (3.5)
(3.5)
15,16 .Локальная и интегральная теоремы Лапласа.В схеме Бернулли распределение вероятностей - биномиальное. При большом количестве проводимых испытаний биномиальное распределение приближается к нормальному с параметрами a = np, σ = √(npq). На этом факте и основано применение приближённых формул Лапласа. Условия применения формул - схема Бернулли (проводимые испытания независимы, вероятность наступления события в каждом испытании постоянна). Тогда вероятность того, что при n испытаниях интересующее нас событие наступит ровно k раз (безразлично, в какой последовательности), приближённо равна

17. понятие случайной величины. дискретные и непрерывные случайные величины
Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Выпадение некоторого значения случайной величины Х это случайное событие: Х = хi. Среди случайных величин выделяют дискретные и непрерывные случайные величины.
| x1 | x2 | … | xn |
| p1 | p2 | … | pn |
Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.
Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.Любая случайная величина имеет свой закон распределения вероятностей и свою функцию распределения вероятностей. Прежде, чем дать определение функции распределения, рассмотрим переменные, которые её определяют.
Случайная величина (непрерывная или дискретная) имеет численные характеристики:
Математическое ожидание М (Х). Эту характеристику можно сравнивать со средним арифметическим наблюдаемых значений случайной величины Х.
Дисперсия D(X). Это характеристика отклонения случайной величины Х от математического ожидания.
Среднее квадратическое отклонение s(Х) для дискретной и непрерывной случайной величины Х – это корень квадратный из ее дисперсии:
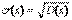 . . |
19. Законы распределения дискретных случайных величин. Так как дискретная случайная величина имеет конечное или счётное множество значений, то их можно просто перечислить и указать соответствующие вероятности. Это можно сделать, например, в форме таблицы
| X | x1 | x2 | ... | xn | ... |
| P | p1 | p2 | pn |
где,  - вероятностьтого, что X примет значение x
- вероятностьтого, что X примет значение x  . Такую таблицу называют рядом распределения.
. Такую таблицу называют рядом распределения.
События  … несовместимы и в результате опыта одно из них обязательно происходит. Из этого следует
… несовместимы и в результате опыта одно из них обязательно происходит. Из этого следует 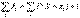
2). Биномиальный закон распределения. Случайная величина может принимать значения 0,1,2,…,n и каждому значению X=m соответствует вероятность 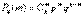 , где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону можно назвать числом появлении события в n независимых опытах.
, где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону можно назвать числом появлении события в n независимых опытах.
З). Пуассоновский закон распределения. Случайная велbчина имеет возможные значения 0,1,2,3,…… и каждому значению Х=m соответствует вероятность 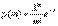 ,где
,где 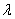 - некоторый параметр, вероятностный смысл которого будет указан несколько страниц спустя.
- некоторый параметр, вероятностный смысл которого будет указан несколько страниц спустя.
4). Гипергеометрический закон распределения. Возможные значения X: 0,1,…,n. И каждому значению X=m соответствует вероятность P(X=m)=P  =
=  .
.  Эта случайная величина, например, равна числу m бракованных изделий среди n взятых наугад из партии объёма N,содержащей M бракованных изделий.
Эта случайная величина, например, равна числу m бракованных изделий среди n взятых наугад из партии объёма N,содержащей M бракованных изделий.
18. Дискретная случайная величина и закон ее распределения
Реальное содержание понятия «случайная величина» может быть выражено с помощью такого определения: случайной величиной, связанной с данным опытом, называетсявеличина, которая при каждом осуществлении этого опыта принимает то или иное числовое значение, причем заранее неизвестно, какое именно. Случайные величиныбудем обозначать буквами  Определение. Говорят, что задана дискретная случайная величина
Определение. Говорят, что задана дискретная случайная величина 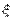 , если указано конечное или счетное множество чисел
, если указано конечное или счетное множество чисел
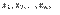 и каждому из этих чисел
и каждому из этих чисел  поставлено в соответствие некоторое положительное число
поставлено в соответствие некоторое положительное число 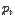 , причем
, причем

Числа 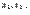 называются возможными значениями случайной величины
называются возможными значениями случайной величины  , а числа
, а числа 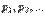 - вероятностями этих значений (
- вероятностями этих значений (  ).Таблица
).Таблица
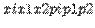 называется законом распределения дискретной случайной величины
называется законом распределения дискретной случайной величины  .
.
Если возможными значениями дискретной случайной величины  являются 0, 1, 2, …, n, а соответствующие им вероятности вычисляются по формуле Бернулли:
являются 0, 1, 2, …, n, а соответствующие им вероятности вычисляются по формуле Бернулли:

то говорят, что случайная величина  имеет биномиальный закон распределения:
имеет биномиальный закон распределения:
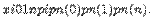
Пусть заданы натуральные числа m, n, s, причем 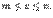 Если возможными значениями дискретной случайной величины
Если возможными значениями дискретной случайной величины  являются 0,1,2,…, m, а соответствующие им вероятности выражаются по формуле
являются 0,1,2,…, m, а соответствующие им вероятности выражаются по формуле

то говорят, что случайная величина  имеет гипергеометрический закон распределения.
имеет гипергеометрический закон распределения.
Другими часто встречающимися примерами законов распределения дискретной случайной величины являются:
геометрический
 где
где  ;
;
Закон распределения Пуассона:
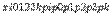
где 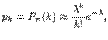
 - положительное постоянное.
- положительное постоянное.
Закон распределения Пуассона является предельным для биномиального при  ,
, 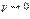 ,
,  . Виду этого обстоятельства при больших n и малых p биномиальные вероятности вычисляются приближенно по формуле Пуассона:
. Виду этого обстоятельства при больших n и малых p биномиальные вероятности вычисляются приближенно по формуле Пуассона:
 где
где 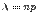 .
.
20. Характеристикой среднего значения случайной величины является математическое ожидание.
Математическим ожиданием M(x) дискретной случайной величины X называется сумма произведений всех ее значений на их вероятности.
M(X) = a = x1p1 + x2p2 + … + xnpn = 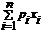
Математическое ожидание обладает следующими свойствами.1. Математическое ожидание постоянной величины равно самой постоянной:M(c) = c.
2. Постоянный множитель можно выносить за знак математического ожидания:M(kX) = kM(X).
3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий:M(X ± Y) = M(X) ± M(Y).
4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:M(XY) = M(X) 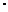 M(Y).
M(Y).
5. Математическое ожидание отклонения случайной величины от ее математического ожидания (X – M(X)) равно нулю:M(X – M(X)) = 0.
21/ Дисперсией D(X) случайной величины X называется математическое ожидание квадрата ее отклонения от математического ожидани D(X) = M[X – M(X)]2
Дисперсию удобно вычислять по формуле D(X) = M(X2) – [M(X)]2
Дисперсия обладает следующими свойствами.1. Дисперсия постоянной величины равна нулю:D(c) = 0.
2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат:D(kX) = k2D(X).
3. Дисперсия суммы независимых случайных величин равна сумме их дисперсий:D(X ± Y) = D(X) + D(Y).
Наряду с дисперсией в качестве показателя рассеяния случайной величины используют среднее квадратическое отклонение  , определяемое по формуле
, определяемое по формуле 
22.Функция распределения случайной величины.
Для описания закона распределения случайной величины X можно рассматривать не вероятность события X=x, а вероятность события X < x, где x – переменная..Функцией распределения случайной величины X называется функция F(x), определяющая для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x: F(X) = P(X < x)
Функция распределения обладает следующими свойствами.
1. Значения F(x) принадлежат отрезку [0;1]: 0 ≤ F(x) ≤ 1.
2. Функция F(x) является неубывающей функцией: F(x2) ≥ F(x1), если x2 > x1.
3. Вероятность попадания случайной величины X в интервал [x1,x2) равна приращению F(x) на этом интервале: P(x1 ≤ X < x2) = F(x2) – F(x1).
4. Если все возможные значения случайной величины X принадлежат интервалу (a,b), то F(x) = 0 при x ≤ a и F(x) = 1 при x ≥ b.
Рис. 1.5. Доверительный интервал
Замечание. Если число g = 0,95, это означает, что в среднем в 95 случаях из 100 интервал Ig накроет параметр θ и в 5 случаях из 100 не накроет его.
Оценка 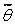 , будучи функцией случайной выборки, является случайной величиной, ε также случайна: ее значение зависит от вероятности γ и, как правило, от выборки. Поэтому доверительный интервал случаен и выражение (1.11) следует читать так: «Интервал (
, будучи функцией случайной выборки, является случайной величиной, ε также случайна: ее значение зависит от вероятности γ и, как правило, от выборки. Поэтому доверительный интервал случаен и выражение (1.11) следует читать так: «Интервал ( 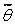 –ε,
–ε, 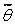 +ε) накроет параметр θ с вероятностью γ»,а не «Параметр θ попадет в интервал (
+ε) накроет параметр θ с вероятностью γ»,а не «Параметр θ попадет в интервал ( 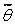 –ε,
–ε, 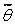 +ε) с вероятностью γ».
+ε) с вероятностью γ».
Дана выборка (x1, x2, …, xn) объема n из генеральной совокупности с генеральным средним mx (неизвестный параметр) и генеральной дисперсией s2 (известна). Ищется интервал [Θ1, Θ2], в котором mx может находиться с доверительной вероятностью γ. Задача может быть решена двумя путями.
I. Предполагая, что предварительно определена точечная оценка mx – выборочное среднее 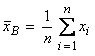 , в качестве статистики для получения Θ1 = = Θ1(x1, x2, …, xn) и Θ2 = Θ2 (x1, x2, …,xn) традиционно рассматривается нормированное выборочное среднее
, в качестве статистики для получения Θ1 = = Θ1(x1, x2, …, xn) и Θ2 = Θ2 (x1, x2, …,xn) традиционно рассматривается нормированное выборочное среднее
z = 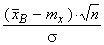 .
.
Случайная величина z имеет распределение:
1. нормальное, с нулевым математическим ожиданием и единичной дисперсией (z 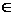 N(0, 1)), если выборка берется из нормальной генеральной совокупности;
N(0, 1)), если выборка берется из нормальной генеральной совокупности;
2. асимптотически нормальное (z 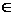 ~N(0, 1)), если генеральная совокупность имеет распределение, отличное от нормального.
~N(0, 1)), если генеральная совокупность имеет распределение, отличное от нормального.
55-???
Критерий согласия Пирсона
Критерий согласия Пирсона (χ2) применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению F(x) при большом объеме выборки (n ≥ 100). Критерий применим для любых видов функции F(x), даже при неизвестных значениях их параметров, что обычно имеет место при анализе результатов механических испытаний. В этом заключается его универсальность.
Использование критерия χ2 предусматривает разбиение размаха варьирования выборки на интервалы и определения числа наблюдений (частоты) nj для каждого из e интервалов. Для удобства оценок параметров распределения интервалы выбирают одинаковой длины.
Число интервалов зависит от объема выборки. Обычно принимают: при n = 100 e = 10 ÷ 15, при n = 200 e = 15 ÷ 20, при n = 400 e = 25 ÷ 30, при n = 1000 e = 35 ÷ 40.
Интервалы, содержащие менее пяти наблюдений, объединяют с соседними. Однако, если число таких интервалов составляет менее 20 % от их общего количества, допускаются интервалы с частотой nj ≥ 2.
Статистикой критерия Пирсона служит величина
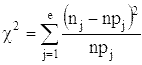 , (3.91)
, (3.91)
где pj - вероятность попадания изучаемой случайной величины в j-и интервал, вычисляемая в соответствии с гипотетическим законом распределением F(x). При вычислении вероятности pj нужно иметь в виду, что левая граница первого интервала и правая последнего должны совпадать с границами области возможных значений случайной величины. Например, при нормальном распределении первый интервал простирается до -∞, а последний - до +∞.
Нулевую гипотезу о соответствии выборочного распределения теоретическому закону F(x) проверяют путем сравнения вычисленной по формуле (3.91) величины с критическим значением χ2α, найденным по табл. VI приложения для уровня значимости α и числа степеней свободы k = e1 - m - 1. Здесь e1 - число интервалов после объединения; m - число параметров, оцениваемых по рассматриваемой выборке. Если выполняется неравенство
χ2 ≤ χ2α (3.92)
то нулевую гипотезу не отвергают. При несоблюдении указанного неравенства принимают альтернативную гипотезу о принадлежности выборки неизвестному распределению.
Недостатком критерия согласия Пирсона является потеря части первоначальной информации, связанная с необходимостью группировки результатов наблюдений в интервалы и объединения отдельных интервалов с малым числом наблюдений. В связи с этим рекомендуется дополнять проверку соответствия распределений по критерию χ2 другими критериями. Особенно это необходимо при сравнительно малом объеме выборки (n ≈ 100).
Критерий согласия Пирсона 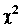 – один из основных:
– один из основных:
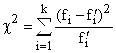
где k – число групп, на которые разбито эмпирическое распределение,
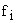 – наблюдаемая частота признака в i-й группе,
– наблюдаемая частота признака в i-й группе,
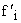 – теоретическая частота.
– теоретическая частота.
Основные понятия теории графов.
|
вероятность появления хотя бы одного события.
Вероятность наступления события А, состоящего в появлении хотя бы одного из событий А1, А2,..., Аn,независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий

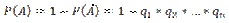
Ч а с т н ы й с л у ч а й. Если события А1 , А2 , ..., Аn имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий
P (A) = l — qn.
12. Формула полной вероятности и формула Байеса
Если событие А может произойти только при выполнении одного из событий 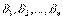 , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
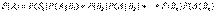 .Эта формула называется формулой полной вероятности.
.Эта формула называется формулой полной вероятности.
Вновь рассмотрим полную группу несовместных событий  , вероятности появления которых
, вероятности появления которых  . Событие А может произойти только вместе с каким-либо из событий
. Событие А может произойти только вместе с каким-либо из событий  , которые будем называть гипотезами. Тогда по формуле полной вероятности
, которые будем называть гипотезами. Тогда по формуле полной вероятности
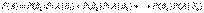
Если событие А произошло, то это может изменить вероятности гипотез  .
.
По теореме умножения вероятностей
 ,
,
откуда 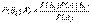 .
.
Аналогично, для остальных гипотез
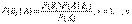
Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез  называются апостериорными вероятностями, тогда как
называются апостериорными вероятностями, тогда как  - априорными вероятностями
- априорными вероятностями
13. независимые испытания. Формула Бернулли
При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний илисхемой Бернулли.
Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А в единичном испытании буквой р, т.е. p=P(A), а вероятность противоположного события (событие А не наступило) - буквой q=P(A¯¯¯)=1−p.
Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражаетсяформулой Бернулли
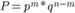
где 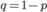 .
.
Так как рассматривалась только одна из возможных комбинаций, когда событие 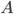 произошло только в первых
произошло только в первых 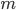 испытаниях, то для определения искомой вероятности нужно перебрать все возможные комбинации. Их число будет равно числу сочетаний из
испытаниях, то для определения искомой вероятности нужно перебрать все возможные комбинации. Их число будет равно числу сочетаний из 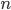 элементов по
элементов по 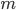 , т.е.
, т.е.  .
.
Таким образом, вероятность того, что событие 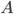 наступит ровно в
наступит ровно в 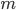 испытаниях определяется по формуле
испытаниях определяется по формуле
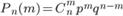 , (3.3)
, (3.3)
где 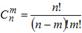 .
.
14. Пуассон
Теорема. Если вероятность  наступления события
наступления события 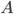 в каждом испытании постоянна и мала, а число независимых испытаний
в каждом испытании постоянна и мала, а число независимых испытаний 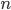 достаточно велико, то вероятность наступления события
достаточно велико, то вероятность наступления события 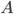 ровно
ровно 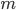 раз приближенно равна
раз приближенно равна
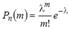 ,(3.4)
,(3.4)
где  .
.
Доказательство. Пусть даны вероятность наступления события 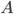 в одном испытании
в одном испытании  и число независимых испытаний
и число независимых испытаний 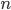 . Обозначим
. Обозначим 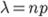 . Откуда
. Откуда 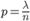 . Подставим это выражение в формулу Бернулли:
. Подставим это выражение в формулу Бернулли:
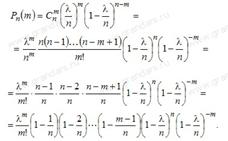
При достаточно большом !!n,, и сравнительно небольшом !!m,, все скобки, за исключением предпоследней, можно принять равными единице, т.е.

Учитывая то, что 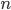 достаточно велико, правую часть этого выражения можно рассмотреть при
достаточно велико, правую часть этого выражения можно рассмотреть при  , т.е. найти предел
, т.е. найти предел

Тогда получим
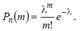 (3.5)
(3.5)
15,16 .Локальная и интегральная теоремы Лапласа.В схеме Бернулли распределение вероятностей - биномиальное. При большом количестве проводимых испытаний биномиальное распределение приближается к нормальному с параметрами a = np, σ = √(npq). На этом факте и основано применение приближённых формул Лапласа. Условия применения формул - схема Бернулли (проводимые испытания независимы, вероятность наступления события в каждом испытании постоянна). Тогда вероятность того, что при n испытаниях интересующее нас событие наступит ровно k раз (безразлично, в какой последовательности), приближённо равна

17. понятие случайной величины. дискретные и непрерывные случайные величины
Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Выпадение некоторого значения случайной величины Х это случайное событие: Х = хi. Среди случайных величин выделяют дискретные и непрерывные случайные величины.
| x1 | x2 | … | xn |
| p1 | p2 | … | pn |
Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.
Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.Любая случайная величина имеет свой закон распределения вероятностей и свою функцию распределения вероятностей. Прежде, чем дать определение функции распределения, рассмотрим переменные, которые её определяют.
Случайная величина (непрерывная или дискретная) имеет численные характеристики:
Математическое ожидание М (Х). Эту характеристику можно сравнивать со средним арифметическим наблюдаемых значений случайной величины Х.
Дисперсия D(X). Это характеристика отклонения случайной величины Х от математического ожидания.
Среднее квадратическое отклонение s(Х) для дискретной и непрерывной случайной величины Х – это корень квадратный из ее дисперсии:
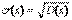 . . |
19. Законы распределения дискретных случайных величин. Так как дискретная случайная величина имеет конечное или счётное множество значений, то их можно просто перечислить и указать соответствующие вероятности. Это можно сделать, например, в форме таблицы
| X | x1 | x2 | ... | xn | ... |
| P | p1 | p2 | pn |
где,  - вероятностьтого, что X примет значение x
- вероятностьтого, что X примет значение x  . Такую таблицу называют рядом распределения.
. Такую таблицу называют рядом распределения.
События  … несовместимы и в результате опыта одно из них обязательно происходит. Из этого следует
… несовместимы и в результате опыта одно из них обязательно происходит. Из этого следует 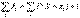
2). Биномиальный закон распределения. Случайная величина может принимать значения 0,1,2,…,n и каждому значению X=m соответствует вероятность 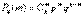 , где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону можно назвать числом появлении события в n независимых опытах.
, где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону можно назвать числом появлении события в n независимых опытах.
З). Пуассоновский закон распределения. Случайная велbчина имеет возможные значения 0,1,2,3,…… и каждому значению Х=m соответствует вероятность 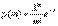 ,где
,где 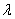 - некоторый параметр, вероятностный смысл которого будет указан несколько страниц спустя.
- некоторый параметр, вероятностный смысл которого будет указан несколько страниц спустя.
4). Гипергеометрический закон распределения. Возможные значения X: 0,1,…,n. И каждому значению X=m соответствует вероятность P(X=m)=P  =
=  .
.  Эта случайная величина, например, равна числу m бракованных изделий среди n взятых наугад из партии объёма N,содержащей M бракованных изделий.
Эта случайная величина, например, равна числу m бракованных изделий среди n взятых наугад из партии объёма N,содержащей M бракованных изделий.
18. Дискретная случайная величина и закон ее распределения
Реальное содержание понятия «случайная величина» может быть выражено с помощью такого определения: случайной величиной, связанной с данным опытом, называетсявеличина, которая при каждом осуществлении этого опыта принимает то или иное числовое значение, причем заранее неизвестно, какое именно. Случайные величиныбудем обозначать буквами  Определение. Говорят, что задана дискретная случайная величина
Определение. Говорят, что задана дискретная случайная величина 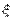 , если указано конечное или счетное множество чисел
, если указано конечное или счетное множество чисел
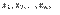 и каждому из этих чисел
и каждому из этих чисел  поставлено в соответствие некоторое положительное число
поставлено в соответствие некоторое положительное число 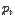 , причем
, причем

Числа 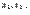 называются возможными значениями случайной величины
называются возможными значениями случайной величины  , а числа
, а числа 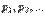 - вероятностями этих значений (
- вероятностями этих значений (  ).Таблица
).Таблица
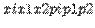 называется законом распределения дискретной случайной величины
называется законом распределения дискретной случайной величины  .
.
Если возможными значениями дискретной случайной величины  являются 0, 1, 2, …, n, а соответствующие им вероятности вычисляются по формуле Бернулли:
являются 0, 1, 2, …, n, а соответствующие им вероятности вычисляются по формуле Бернулли:

то говорят, что случайная величина  имеет биномиальный закон распределения:
имеет биномиальный закон распределения:
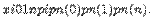
Пусть заданы натуральные числа m, n, s, причем 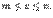 Если возможными значениями дискретной случайной величины
Если возможными значениями дискретной случайной величины  являются 0,1,2,…, m, а соответствующие им вероятности выражаются по формуле
являются 0,1,2,…, m, а соответствующие им вероятности выражаются по формуле

то говорят, что случайная величина  имеет гипергеометрический закон распределения.
имеет гипергеометрический закон распределения.
Другими часто встречающимися примерами законов распределения дискретной случайной величины являются:
геометрический
 где
где  ;
;
Закон распределения Пуассона:
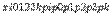
где 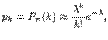
 - положительное постоянное.
- положительное постоянное.
Закон распределения Пуассона является предельным для биномиального при  ,
, 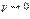 ,
,  . Виду этого обстоятельства при больших n и малых p биномиальные вероятности вычисляются приближенно по формуле Пуассона:
. Виду этого обстоятельства при больших n и малых p биномиальные вероятности вычисляются приближенно по формуле Пуассона:
 где
где 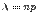 .
.
20. Характеристикой среднего значения случайной величины является математическое ожидание.
Математическим ожиданием M(x) дискретной случайной величины X называется сумма произведений всех ее значений на их вероятности.
M(X) = a = x1p1 + x2p2 + … + xnpn = 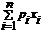
Математическое ожидание обладает следующими свойствами.1. Математическое ожидание постоянной величины равно самой постоянной:M(c) = c.
2. Постоянный множитель можно выносить за знак математического ожидания:M(kX) = kM(X).
3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий:M(X ± Y) = M(X) ± M(Y).
4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:M(XY) = M(X) 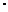 M(Y).
M(Y).
5. Математическое ожидание отклонения случайной величины от ее математического ожидания (X – M(X)) равно нулю:M(X – M(X)) = 0.
21/ Дисперсией D(X) случайной величины X называется математическое ожидание квадрата ее отклонения от математического ожидани D(X) = M[X – M(X)]2
Дисперсию удобно вычислять по формуле D(X) = M(X2) – [M(X)]2
Дисперсия обладает следующими свойствами.1. Дисперсия постоянной величины равна нулю:D(c) = 0.
2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат:D(kX) = k2D(X).
3. Дисперсия суммы независимых случайных величин равна сумме их дисперсий:D(X ± Y) = D(X) + D(Y).
Наряду с дисперсией в качестве показателя рассеяния случайной величины используют среднее квадратическое отклонение  , определяемое по формуле
, определяемое по формуле 
22.Функция распределения случайной величины.
Для описания закон

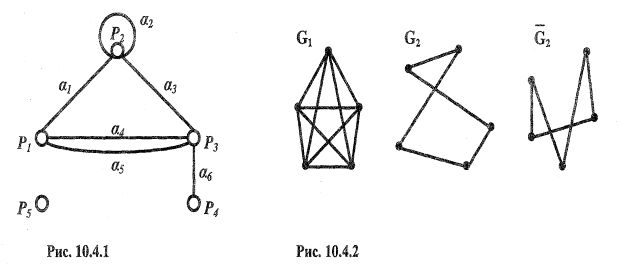 Ребра, имеющие одинаковые концевые вершины, называются параллельными. Ребро, концевые вершины которого совпадают, называется петлей. На рис. 10.4.1 а4 и а5 — параллельные ребра, a а6 — петля. Вершина и ребро называются инцидентными друг другу, если вершина является для этого ребра концевой точкой. На рис. 10.4.1 вершина Р3 и ребро а3инцидентны друг другу. Две вершины, являющиеся концевыми для некоторого ребра, называются смежными вершинами. Два ребра, инцидентные одной и той же вершине, называются смежными ребрами. На рис. 10.4.1 Р1 , Р2 — смежные вершины, а а1, а4 — смежные ребра. Степенью вершины называется число ребер, инцидентных ей. Вершина степени 1 называется висячей. Вершина степени 0 называется изолированной. На рис. 10.4.1 степень вершины Р1 равна трем, Р4 —висячая вершина, Р5 —изолированная. Теорема 1. В графе G сумма степеней всех его вершин — число четное, равное удвоенному числу ребер графа:
Ребра, имеющие одинаковые концевые вершины, называются параллельными. Ребро, концевые вершины которого совпадают, называется петлей. На рис. 10.4.1 а4 и а5 — параллельные ребра, a а6 — петля. Вершина и ребро называются инцидентными друг другу, если вершина является для этого ребра концевой точкой. На рис. 10.4.1 вершина Р3 и ребро а3инцидентны друг другу. Две вершины, являющиеся концевыми для некоторого ребра, называются смежными вершинами. Два ребра, инцидентные одной и той же вершине, называются смежными ребрами. На рис. 10.4.1 Р1 , Р2 — смежные вершины, а а1, а4 — смежные ребра. Степенью вершины называется число ребер, инцидентных ей. Вершина степени 1 называется висячей. Вершина степени 0 называется изолированной. На рис. 10.4.1 степень вершины Р1 равна трем, Р4 —висячая вершина, Р5 —изолированная. Теорема 1. В графе G сумма степеней всех его вершин — число четное, равное удвоенному числу ребер графа: 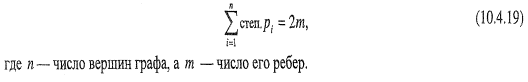 Теорема 2. Число нечетных вершин любого графа, т.е. вершин, имеющих нечетную степень, четно. Граф G называется полным, если любые две его различные вершины соединены ребром и'он не содержит параллельных ребер. Дополнением графа G называется граф
Теорема 2. Число нечетных вершин любого графа, т.е. вершин, имеющих нечетную степень, четно. Граф G называется полным, если любые две его различные вершины соединены ребром и'он не содержит параллельных ребер. Дополнением графа G называется граф 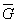 с теми же вершинами, что и граф G, и содержащий, только те ребра, которые нужно добавить к графу G, чтобы получился полный граф. На рис. 10.4.2 изображены следующие графы: G1 — полный граф с пятью вершинами, G2 — некоторый граф, имеющий пять вершин,
с теми же вершинами, что и граф G, и содержащий, только те ребра, которые нужно добавить к графу G, чтобы получился полный граф. На рис. 10.4.2 изображены следующие графы: G1 — полный граф с пятью вершинами, G2 — некоторый граф, имеющий пять вершин,