Случайные события. Алгебра событий.

Аксиоматическое определение вероятности

Отправным пунктом аксиоматики А.Н. Колмогорова является множество элементарных событий ω, в специальной литературе называемое фазовым пространством и традиционно обозна-чаемое через Ω. Любое наблюдаемое событие, вероятность которого необходимо определить, представимо в виде некоторого подмножества фазового пространства. Поэтому наряду с множеством Ω рассматривается множество Θ подмножеств элементарных событий, символическое обозначение которого может быть произвольным. Достоверное событие представимо всем фазовым пространством. Множество Θ называется алгеброй множеств, если выполнены следующие требования:

1) Ω ∈ Θ, ∅∈ Θ;

2) из того, что A ∈ Ω, следует, что так же ∈ Θ;

3) из того, что A ∈ Θ и B ∈ Θ, следует, что A ∪ B ∈ Θ и A ∩ B∈ Θ.

Если дополнительно к перечисленным выполняется еще следующее требование:

4) из того, что An∈ Θ (при n = 1,2...), вытекает, что

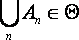
то множество Θ называется σ-алгеброй. Элементы Θ называются случайными событиями.

Под операциями над случайными событиями в аксиоматической теории вероятностей понимаются операции над соответствующими множествами. В результате можно установить взаимное соответствие между терминами языка теории множеств и языка теории вероятностей [23].

В качестве аксиом, определяющих вероятность, А.Н. Колмогоровым приняты следующие утверждения:

Аксиома 1. Каждому случайному событию А поставлено в соответствие неотрицательное число P (A) , называемое его вероятностью.

Аксиома 2. P(Ω)= 1.

Аксиома 3 (аксиома сложения). Если события A1, A2,...,An попарно несовместимы, то

P(A1 + A2 +...+ An) = P(A1) + P(A2) +...+ P(An).

Следствиями сформулированных аксиом являются следующие утверждения.

1. Вероятность невозможного события равна нулю: P(∅) = 0.

2. Для любого события АP(А)) = 1 - P(A).

3. Каково бы ни было случайное событие А, 0 ≤ P(A) ≤ 1.

4. Если событие А влечет за собой событие В, то P(A) ≤ P(B).

Вероятностным пространством принято называть тройку символов {Ω, Θ, P}, где Ω – множество элементарных событий ω, Θ – σ – алгебра подмножеств Ω, называемых случайными событиями, и P(A) - вероятность, определенная на σ – алгебре Θ.

Таким образом, согласно аксиоматике А.Н. Колмогорова каждому наблюдаемому событию приписывается некоторое неотрицательное число, называемое вероятностью этого события, так, чтобы вероятность всего фазового пространства была равна 1, и выполнялось свойство сигма-аддитивности. Последнее свойство означает, что в случае попарно исключающих друг друга событий вероятность наступления по крайней мере одного (и в силу попарной несовместимости, ровно одного) наблюдаемого события совпадает с суммой вероятностей наблюдаемых событий из данной конечной или счетной совокупности наблюдаемых событий.

Теорема Пуассона.

Свойства случайной величины

Свойства плотности вероятности

Числовые характеристика случайных величин.

Случайные события. Алгебра событий.

Алгебра событий (в теории вероятностей) — алгебра подмножеств пространства элементарных событий 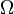, элементами которого служат элементарные события.

Как и положено алгебре множеств алгебра событий содержит невозможное событие (пустое множество) и замкнута относительно теоретико-множественных операций, производимых в конечном числе. Достаточно потребовать, чтобы алгебра событий была замкнута относительно двух операций, например, пересечения и дополнения, из чего сразу последует её замкнутость относительно любых других теоретико-множественных операций. Алгебра событий, замкнутая относительно счётного числа теоретико-множественных операций, называется сигма-алгеброй событий.

В теории вероятностей встречаются следующие алгебры и сигма-алгебры событий:

1) алгебра конечных подмножеств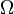

2) сигма-алгебра счётных подмножеств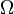

3) алгебра подмножеств 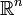, образованная конечными объединениями интервалов;

4) сигма-алгебра борелевских подмножеств топологического пространства 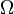, то есть наименьшая сигма-алгебра, содержащая все открытые подмножества .

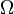5) алгебра цилиндров в пространстве функций и сигма-алгебра, ими порожденная.

Алгебры и сигма-алгебры событий — это области определения вероятности 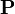. Если 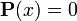, то событие 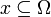называется невозможным событием; если 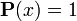, то событие 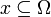называется достоверным событием;

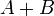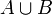Событие или ,заключается в том, что из двух событи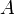й и 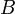происходит по крайней мере одно, называется суммой событи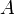й и .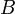

Любая сигма-аддитивная вероятность на алгебре событий однозначно продолжается до сигма-аддитивной вероятности, определенной на сигма-алгебре событий, порожденной данной алгеброй событий.

Случа́йноесобы́тие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.

Случайное событие, которое никогда не реализуется в результате случайного эксперимента, называется невозможным и обозначается символом 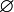. Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом .

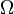2. Классическое и статистическое определения вероятности. Геометрические вероятности.

Классическое определение.

Событие – это факт, который в результате опыта может произойти или не произойти.

Вероятность - это одно из основных понятий теории вероятности.

Вероятностью события называется численная мера степени объективной возможности этого события. Вероятность события А обозначается Р (А).

Достоверным называется событие В, которое в результате опыта непременно должно произойти:

Р (В) = 1

Невозможным называется событие С, которое в результате опыта не может произойти:

Р (С) = 0

Вероятность любого события А заключена между нулем и единицей:

0 ≤ Р(А) ≤ 1

Полной группой событий называется несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно из них. Сумма вероятностей событий, образующих полную группу, равна 1.

Несколько событий называются несовместимыми, если никакие два из них не могут появиться вместе. Пример.

Несколько событий называются равновозможными, если по условиям опыта нет оснований считать какое-либо из них более возможным, чем любое другое.

Если несколько событий: образуют полную группу, несовместны и равновозможны, то они называются случаями.

Случай называется благоприятным событию, если появление этого случая влечет за собой появление события.

Вероятность события А вычисляется по формуле:

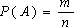
где n – общее число случаев, m – число случаев, благоприятных событию А.

Определение: вероятностью события А называют отношение числа благоприятствующих этому событию случаев к общему числу всех равновозможных элементарных исходов, образующих полную группу.

Статистическое определение вероятности.

При рассмотрении результатов отдельных испытаний очень трудно найти какие-либо закономерности. Однако в последовательности одинаковых испытаний можно обнаружить устойчивость некоторых средних характеристик. Частостью какого-либо события в данной серии из n испытаний называется отношение m/n, числа m тех испытаний, в которых событие А наступило, к общему числу испытаний n. Почти в каждой достаточно длинной серии испытаний частость события А устанавливается около определенного значения 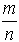, которое принимается за вероятность события А. Устойчивость значения частости подтверждается специальными экспериментами. Статистические закономерности такого рода были впервые обнаружены на примере азартных игр, т. е. на примере тех испытаний, которые характеризуются равновозможностью исходов. Это открыло путь для статистического подхода к численному определению вероятности, когда нарушается условие симметрии эксперимента. Частость события А называют статистической вероятностью, которая обозначается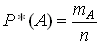

где mA - число экспериментов, в которых появилось событие А;

n - общее число экспериментов.

Формулы (1.1) и (1.2) для определения вероятности имеют внешнее сходство, но они различны по существу. Формула (1.1) служит для теоретического вычисления вероятности события по заданным условиям опыта. Формула (1.2) служит для экспериментального определения частости события. Чтобы воспользоваться формулой (1.2), необходим опытный статистический материал.

Геометрические вероятности.

При геометрическом подходе к определению вероятности в качестве пространства элементарных событий рассматривается произвольное множество конечной лебеговой меры на прямой, плоскости или пространстве. Событиями называются всевозможные измеримые подмножества множества .

Вероятность события А определяется формулой :

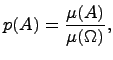
Где 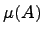обозначает лебегову меру множества А. При таком определении событий и вероятностей все аксиомы А.Н.Колмогорова выполняются.

В конкретных задачах, которые сводятся к указанной выше вероятностной схеме, испытание интерпретируется как случайный выбор точки в некоторой области , а событиеА – как попадание выбранной точки в некоторую подобласть А области .

При этом требуется, чтобы все точки области имели одинаковую возможность быть выбранными. Это требование обычно выражается словами «наудачу», «случайным образом» и т.д.