Модуль 5. Классическая предельная проблема теории вероятностей

1. Какой вид сходимости последовательности случайных величин сильнее: сходимость по распределению, или сходимость по вероятности?

2. Какое требование к последовательностям случайных величин предъявляется во всех теоремах классической предельной проблемы теории вероятностей?

3. Можно ли применять теорему Хинчина к последовательностям одинаково распределённых случайных величин, имеющих конечные дисперсии?

4. Покажите, что теорема Муавра-Лапласа является частным случаем теоремы Леви.

5. Последовательность независимых одинаково распределённых случайных величин подчиняется ЦПТ. Можно ли утверждать, что эта последовательность подчиняется ЗБЧ?

6. Последовательность независимых разно распределённых случайных величин подчиняется ЗБЧ. Можно ли утверждать, что эта последовательность подчиняется ЦПТ?

7. Можно ли утверждать, что теорема Хинчина является частным случаем теоремы Чебышева?

8. Покажите, что из того, что последовательность случайных величин подчиняется условию Ляпунова следует, что онаподчиняется и условию Линдеберга.

9. Покажите, что теорема Муавра-Лапласа является частным случаем теоремы Линдеберга?

10. Покажите, что последовательность независимых разно распределённых бернуллиевских случайных величин подчиняется ЦПТ.

Модуль 6. Первичная обработка статистических данных. Точечные оценки числовых характеристик

1. Каким условием надо руководствоваться для определения числа интервалов при построении вариационного ряда?

2. Могут ли интервалы вариационного ряда иметь разные длины?

3. Можно ли утверждать, что из несмещённости точечной оценки числовой характеристики следует её состоятельность?

4. Будет ли точечная оценка, полученная методом максимального правдоподобия несмещённой оценкой числовой характеристики?

5. Какая теорема применяется при проверке состоятельности точечных оценок начальных моментов исследуемой случайной величины?

6. Может ли точечная оценка дисперсии быть отрицательным числом?

7. При проверке состоятельности оценки 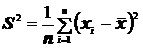применяется лемма, в которой по непрерывной функции 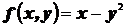строится сходящаяся по вероятности последовательность 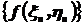, 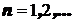. Точечной оценкой коэффициента линейной корреляции будет статистика 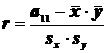, получаемая методом моментов. Постройте непрерывную функцию, с помощью которой, применяя лемму, можно проверить состоятельность этой оценки.

8. У случайной величины отсутствует математическое ожидание. Имеется статистическая выборка значений этой случайной величины. Можно ли утверждать, что у элементов выборки существует конечное среднее арифметическое?

9. Можно ли утверждать, что увеличение объёма выборки приводит к уменьшению величины отличия получаемых значений средних арифметических от значения математического ожидания?

10. Можно ли применять неравенство Рао-Крамера для проверки несмещённости точечной оценки?

Модуль 7. Интервальные оценки числовых характеристик

1. Увеличение объёма выборки при неизменном значении доверительной вероятности приводит к уменьшению длины доверительного интервала. Как будет изменяться доверительная вероятность, если при постоянной длине доверительного интервала будет увеличиваться объём выборки?

2. Покажите, что при увеличении числа n последовательность случайных величин 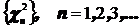сходится по распределению к нормальному закону.

3. Покажите, что при увеличении числа n последовательность случайных величин 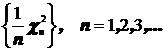сходится по вероятности к единице.

4. Как изменяется длина доверительного интервала при увеличении доверительной вероятности?

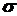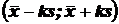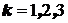5. Известно, что исследуемая случайная величина подчиняется нормальному закону с параметрами mи . Можно ли использовать в качестве доверительных интервалов интервалы , где ? Чему будут равны доверительные вероятности ?

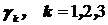Модуль 8. Статистическая проверка гипотез

1. Что называется критерием статистической проверки гипотез?

2. Можно ли выбрать такой критерий, при котором вероятность ошибки первого рода будет равна нулю?

3. Какие распределения вероятностей используются при построении критерия статистической проверки гипотез?

4. Дайте формулировку правила принятия решений?

5. Сколько типов задач рассматривается методами статистической проверки гипотез?

6. По результатам проверки двух гипотез: ,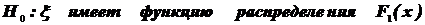

,

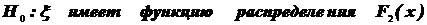где 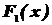и 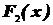- разные функции распределения, по элементам одной и той же выборки, прияты решения о том, что нет оснований отклонять и первую, и вторую гипотезу.

Может ли встретится такая ситуация при применении критерия Пирсона?

7. Может ли увеличение объёма выборки, по которой вычисляется наблюдаемое значение критерия, привести к отмене ранее принятого решения об отклонении основной гипотезы?

8. Можно ли использовать одну и ту же выборку для проверки гипотезы о значении математического ожидания и гипотезы о виде закона распределения исследуемой случайной величины?

9. В результате проверки принято решение об отклонении основной гипотезы и принятии альтернативной гипотезы.

Затем основную гипотезу назвали альтернативной, а альтернативную гипотезу назвали основной. Для того же критерия 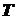, при том же уровне значимости α определены новые област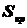и и 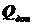. Какое решение будет принято, если будет использована та же выборка?

10. Можно ли проверку знаний студента на экзамене считать статистической проверкой гипотез? Сформулируйте основную и альтернативную гипотезы. Что будет являться критерием проверки справедливости основной гипотезы? Объясните причины ошибок первого и второго рода.