Модуль 1.Вероятностное пространство с не более чем счетным множеством элементарных исходов

Основные понятия: Элементарный исход. Множество элементарных исходов. Алгебра событий. Вероятностная функция. Условная вероятность.

Вероятностное пространство<W,A,P>

Множество элементарных исходовW	Алгебра событийA	Вероятностная функцияP
Примеры	Операции над событиями	Простейшие свойства

1. Классическая модель: ;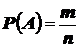

(Урновая схема, различные способы организации выборок).

2. Биномиальная модель (Схема Бернулли): ;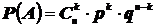

(Полиномиальная модель).

3. Геометрическая модель: ;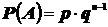

(Отрицательное биномиальное распределение).

Условная вероятность. Попарная независимость событий и независимость событий в совокупности.

Формула полной вероятности. Формула Байеса.(7 часов)

Модуль 2.Общая вероятностная модель. Аксиоматика А.Н. Колмогорова

Основные понятия: σ-алгебра множеств. Измеримое пространство. σ-аддитивная функция множеств. Нормированная функция множеств. Бесконечные множества различной мощности.

Аксиоматическое построение вероятностного пространства <W, A, P>. Свойства вероятностной функции. Борелевские алгебры множеств. Измеримые пространства<R, B (R)>;<Rⁿ, B (Rⁿ)>. Типы и примеры задания вероятностных функций на измеримых пространствах.(6 часов)

Модуль 3.Случайные величины и векторы

Основные понятия: Измеримая функция. Ряд распределения. Плотность вероятности. Компоненты случайного вектора. Согласованность законов распределения вероятностей. Устойчивость законов распределения вероятностей.

Случайная величина - измеримое отображение<W,A >в<R, B (R)>.

Случайный вектор - измеримое отображение<W,A >в<Rⁿ, B (Rⁿ)>.

Типы случайных величин и векторов. Задание законов распределения. Функция распределения случайной величины и случайного вектора. Компоненты случайного вектора. Частные распределения и частные функции распределения. Многомерный нормальный закон. Составной случайный вектор. Независимость случайных величин. Критерий независимости (три формы).

(9 часов)

Модуль 4.Числовые характеристики случайных величин и векторов

Основные понятия: Функция случайной величины. Математическое ожидание. Дисперсия. Начальные и центральные моменты случайных величин и векторов. Ковариационный момент. Коэффициент линейной корреляции.

ИнтегралЛебега-Стилтьеса(Римана-Стилтьеса). Математическое ожидание случайной величины и случайного вектора. Свойства. Примеры. Дисперсия случайной величины. Свойства. Примеры. Начальные и центральные моменты случайной величины и случайного вектора. Ковариационный момент. Ковариационная матрица. Коэффициент линейной корреляции и его свойства. Условные распределения и условные математические ожидания. Линейная регрессия случайных величин.(12 часов)