Теория вероятностей и элементы массового обслуживания. Математическая статистика
Задача 6.1
261. В барабане револьвера восемь гнезд, из которых в шесть вложены патроны, а два пустые. Барабан приводится в движение, в результате чего против ствола оказывается одно из гнезд. После этого нажимается спусковой крючок. Если гнездо пустое, то выстрела не происходит. Найти вероятность того, что в результате двух опытов: а) выстрела не произойдет; б) произойдет два выстрела; в) произойдет хотя бы один выстрел.
262. В лифт двенадцатиэтажного дома вошли 3 человека. Предположим, что каждый из них с равной вероятностью может выйти на любом из этажей, начиная со второго. Найти вероятность того, что все 3 пассажира сойдут на одном этаже; что только два пассажира сойдут на одном этаже.
263. Вероятность хотя бы одного попадания при двух выстрелах равна 0,84. Найти: а) наивероятнейшее число попаданий в серии из 7 выстрелов и модельную вероятность; б) что вероятнее: три попадания при четырех выстрелах или шесть из восьми?
264. Стрелок А поражает мишень с вероятностью 0,6, стрелок В – с вероятностью 0,5 и стрелок С – с вероятностью 0,4. Стрелки дали залп по мишени и две пули попали в цель. Чтовероятнее: попал стрелок С в мишень или нет?
265. В ящике десять стандартных деталей и пять бракованных. Наудачу извлекают три детали. Каковы вероятности того, что среди них: а) одна бракованная; б) две бракованных; в) хотя бы одна стандартная?
266. Имеются две партии однородных деталей. Первая партия состоит из 12 деталей, из которых 3 бракованных. Вторая партия состоит из 15 деталей, из которых 4 бракованных. Из первой и из второй партии извлекают по две детали. Какова вероятность, что среди них нет бракованных деталей?
267. В ящике 100 деталей, из которых 20 изготовлены первым заводом, 80 – вторым. Первый завод производит 90% хороших деталей, второй – 80%. Найти вероятность того, что две извлеченные наудачу детали окажутся хорошими.
268. Из урны, содержащей 3 белых и 2 черных шара, наудачу вынули два шара и положили их во вторую урну, содержащую 4 белых и 4 черных шара. Найти вероятность вынуть белый шар из второй урны.
269. В коробке лежат 9 теннисных мячей, из которых 6 новых. Для первой игры взяли 2 мяча, которые после игры не возвратили. Для второй игры тоже взяли 2 мяча, оказавшиеся новыми. Какова вероятность того, что для первой игры брали два старых мяча?
270. Для изделий некоторого производства вероятность удовлетворять стандарту равна 0,95. Предлагается упрощенная система испытаний, дающая положительный результат с вероятностью 0,98 для изделий, удовлетворяющих стандарту, а для изделий не удовлетворяющих стандарту, с вероятностью 0,05. Какова вероятность того, что изделие, выдержавшее испытание, удовлетворяет стандарту?
Задача 6.2
Задана непрерывная случайная величина Х своей плотностью распределения f(x). Требуется:
1. определить коэффициент А;
2. найти функцию распределения F(x);
3. схематично построить графики функций f(x) и F(x);
4. вычислить математическое ожидание и дисперсию X;
5. определить вероятность того, что Х примет значение из интервала (а, b).
Решение проверить в MathCad.
271. f(x) = 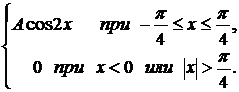 a =
a = 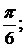 b = 2.
b = 2.
272. f(x) = 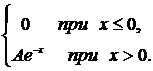 a = 1; b =+
a = 1; b =+ 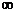 .
.
273. f(x) = 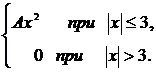 a =1; b = 2.
a =1; b = 2.
274. f(x) = 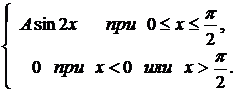 a =
a = 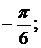 b =
b = 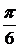 .
.
275. f(x) = 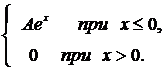 a = –
a = – 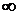 ; b =–1.
; b =–1.
Задана непрерывная случайная величина Х своей функцией распределения F(x). Требуется:
1. определить коэффициент А;
2. найти плотность распределения вероятностей f(x);
3. схематично построить графики функций f(x) и F(x);
4. вычислить математическое ожидание и дисперсию X;
5. определить вероятность того, что Х примет значение из интервала (а, b).
Решение проверить в MathCad.
276. F(x) =  a =1; b =2.
a =1; b =2.
277. F(x) = 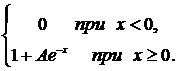 a =1; b = +
a =1; b = + 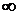 .
.
278. F(x) = 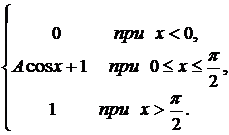 a =
a = 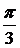 ; b =
; b = 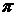 .
.
279. F(x) = 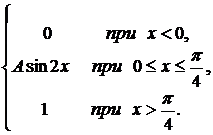 a = 0; b =
a = 0; b = 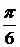 .
.
280. F(x) = 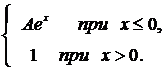 a = –
a = – 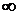 ; b =–1.
; b =–1.
Задача 6.3
Нормально распределенная случайная величина Х задана своими параметрами 
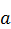 (математическое ожидание) и
(математическое ожидание) и 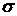 (среднее квадратическое отклонение). Требуется:
(среднее квадратическое отклонение). Требуется:
а) написать плотность вероятности и схематически изобразить ее график;
б) найти вероятность того, что Х примет значение из интервала ( 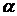 ;
; 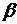 );
); 

в) найти вероятность того, что Х отклонится (по модулю) от а не более чем на 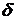 ;
;
г) применяя правило « 3 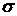 » найти крайние (допустимые) значения случайной величины Х.
» найти крайние (допустимые) значения случайной величины Х.
Решение проверить в MathCad.
281. 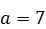 ,
, 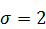 ,
, 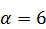 ,
, 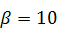 ,
, 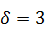 .
.
282. 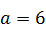 ,
, 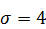 ,
, 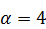 ,
, 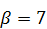 ,
, 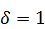 .
.
283. 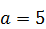 ,
, 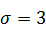 ,
, 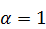 ,
, 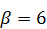 ,
, 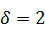 .
.
284. 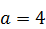 ,
, 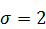 ,
, 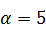 ,
, 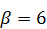 ,
, 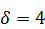 .
.
285. 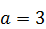 ,
, 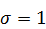 ,
, 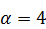 ,
, 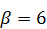 ,
, 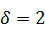 .
.
286. 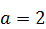 ,
, 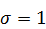 ,
, 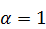 ,
, 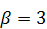 ,
, 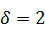 .
.
287. 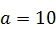 ,
, 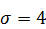 ,
, 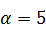 ,
, 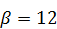 ,
, 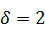 .
.
288. 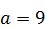 ,
, 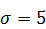 ,
, 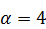 ,
, 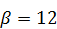 ,
, 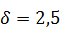 .
.
289. 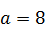 ,
, 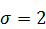 ,
, 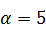 ,
, 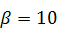 ,
, 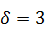 .
.
290. 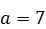 ,
, 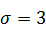 ,
, 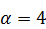 ,
, 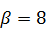 ,
, 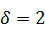 .
.
Задача 6.4
АТС имеет k линий связи. Поток вызовов – простейший с интенсивностью 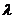 вызовов в минуту. Среднее время переговоров составляет t минут. Время переговоров распределено по показательному закону. Найти: 1) абсолютную и относительную пропускные способности АТС; 2) вероятность того, что все линии связи заняты; 3) среднее число занятых линий связи; 4) определить число линий связи АТС достаточное для того, чтобы вероятность отказа не превышала
вызовов в минуту. Среднее время переговоров составляет t минут. Время переговоров распределено по показательному закону. Найти: 1) абсолютную и относительную пропускные способности АТС; 2) вероятность того, что все линии связи заняты; 3) среднее число занятых линий связи; 4) определить число линий связи АТС достаточное для того, чтобы вероятность отказа не превышала 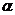 .
.
291. k = 5, 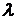 = 0,6, t = 3,5,
= 0,6, t = 3,5, 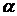 = 0,06.
= 0,06.
292. k = 5, 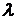 = 0,8, t = 2,9,
= 0,8, t = 2,9, 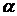 = 0,05.
= 0,05.
293. k = 6, 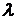 = 0,7, t = 2,7,
= 0,7, t = 2,7, 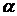 = 0,01.
= 0,01.
294. k = 5, 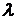 = 0,7, t = 3,5,
= 0,7, t = 3,5, 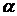 = 0,05.
= 0,05.
295. k = 5, 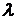 = 0,9, t = 2,5,
= 0,9, t = 2,5, 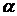 = 0,06.
= 0,06.
296. k = 4, 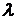 = 0,9, t = 2,1,
= 0,9, t = 2,1, 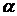 = 0,01.
= 0,01.
297. k = 6, 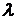 = 0,8, t = 2,2,
= 0,8, t = 2,2, 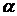 = 0,01.
= 0,01.
298. k = 3, 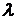 = 0,7, t = 3,1,
= 0,7, t = 3,1, 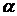 = 0,06.
= 0,06.
299. k = 5, 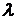 = 0,8, t = 2,6,
= 0,8, t = 2,6, 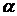 = 0,06.
= 0,06.
300. k = 5, 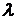 = 0,9, t = 2,8,
= 0,9, t = 2,8, 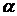 = 0,05.
= 0,05.
Задача 6.5
Данные наблюдений над двумерной случайной величиной (Х, У) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии У на Х. Выполнить чертеж. Решение проверить в MathCad.
301.
| X Y | 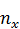 | |||||||
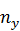 |
302.
| X Y | 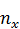 | ||||||
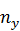 |
303.
| X Y | 9,6 | 9,8 | 10,0 | 10,2 | 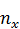 | |
| 19,5 | ||||||
| 20,0 | ||||||
| 20,5 | ||||||
| 21,0 | ||||||
| 21,5 | ||||||
| 22,0 | ||||||
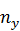 |
304.
| X Y | 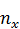 | ||||||
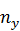 |
305.
| X Y | 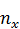 | ||||||
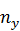 |
306.
| X Y | 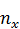 | ||||||
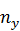 |
307.
| X Y | 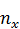 | ||||||
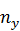 |
308.
| X Y | 2,15 | 3,85 | 5,55 | 7,25 | 8,95 | 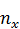 | |
| 1,95 | |||||||
| 3,45 | |||||||
| 4,95 | |||||||
| 6,45 | |||||||
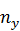 |
309.
| X Y | 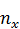 | ||||||||
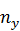 |
310.
| X Y | 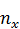 | ||||||
| 6,75 | |||||||
| 8,25 | |||||||
| 9,75 | |||||||
| 11,25 | |||||||
| 12,75 | |||||||
 |
Задача 6.6
Известно эмпирическое распределение выборки объема n случайной величины Х. Проверить гипотезу о распределении по закону Пуассона генеральной совокупности этой величины. Использовать критерий согласия Пирсона (хи–квадрат) при уровне значимости 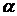 = 0,05.
= 0,05.
| № | 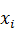 | 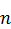 | ||||||
| 311. | 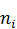 | |||||||
| 312. | 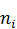 | |||||||
| 313. | 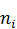 | |||||||
| 314. | 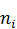 | |||||||
| 315. | 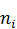 | |||||||
| 316. | 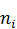 | |||||||
| 317. | 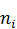 | |||||||
| 318. | 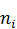 | |||||||
| 319. | 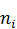 | |||||||
| 320. | 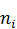 |
После изложения практической части работы студент приводит список литературы, использованной им при написании контрольной работы. В список включаются те источники, которые использовались при подготовке контрольной работы и на которые имеются ссылки в работе.
При описании литературного источника необходимо указать:
· фамилии и инициалы авторов;
· название книги, статьи;
· место издания;
· издательство;
· год издания;
· объем (сведения о количестве страниц).
Ниже приведены примеры описания некоторых видов литературных источников.
Пример. Книга одного и более авторов.
Баврин И.И. Высшая математика: Электронный ресурс. – М.: ООО Академия, 2010.
Информационные технологии в маркетинге / Под ред. Г.А. Титоренко. М.: ЮНИТИ-ДАНА, 2000. - 335 с.
Пример. Статья из журнала.
Коржов В. Internet на космической скорости // Мир ПК, 2001. № 1. С. 86-87.
В приложениях (при необходимости) помещают вспомогательные или дополнительные материалы, которые иллюстрируют текст основной части работы. По форме они могут представлять собой текст, таблицы, графики, диаграммы, схемы, рисунки. Каждое приложение должно начинаться с новой страницы с указанием в правом верхнем углу слова «Приложение» и иметь тематический заголовок. При наличии в работе более одного приложения они нумеруются арабскими цифрами. Связь основного текста с приложениями осуществляется через ссылки (например, см. приложение 5).
Преподаватель, в соответствии с установленным графиком, осуществляет консультирование по выполнению работы. На консультациях студент обсуждает и уточняет содержание теоретической и практической частей контрольной работы.
Завершенная работа сдается преподавателю в установленные учебным графиком сроки на рецензию. Преподаватель оценивает содержание работы, степень самостоятельности ее выполнения, уровень грамотности, в рецензии отмечает положительные стороны работы и ее недостатки и определяет, допускается ли она к защите (собеседованию). Если студент не допущен к защите, то контрольная работа должна быть доработана в соответствии с замечаниям.
Собеседование позволяет выявить уровень знаний студента по выбранной теме, степень его самостоятельности в выполнении работы. В случае необходимости собеседование проводится в компьютерном зале с демонстрацией фрагментов работы на ПК. Результаты собеседования оцениваются на «зачет», «незачет».
В случае незачета студент должен внести необходимые изменения в работу и лучше подготовиться к повторной защите.
