Построение эпюр в плоско-пространственных системах.

Систему, состоящую из прямолинейных стержней, жестко соединенных между собой, расположенных в одной плоскости и нагруженных перпендикулярно к этой плоскости, будем называть плоско-пространственной.

В настоящем пособии будем рассматривать только жесткозащемленые плоско-пространственные системы (далее сокращенно: ППС). При этом возможны два основных варианта:

1. Система располагается горизонтально, нагрузки приложены в вертикальных плоскостях (рис.15,а.,б).

2. Система располагается в вертикальной плоскости, нагрузки приложены горизонтально (рис.15,в,г).

В первом случае (рис.15,а,б) в поперечных сечениях стержней системы могут возникать поперечная сила Q_y, изгибающий момент M_x и крутящий момент M_кр; во втором случае – Q_x, M_y, M_кр. Очевидно, что поворотом на 90 градусов системы второго вида (рис.15,в,г) приводятся к системам первого вида, при этом Q_x переходит в Q_y, M_y - в M_x, поэтому в дальнейшем ограничимся рассмотрением систем первого вида.

Известно, что при одновременном наличии в сечениях изгибаемой стержневой системы внутренних моментов и внутренних сил влияние последних на напряженно-деформированное состояние системы незначительно (исключение составляет "короткие" стержни), поэтому исключим из рассмотрения поперечную силу Q_y.

Итак, остановимся на правилах построения эпюр M_x и M_кр для плоско-пространственных систем.

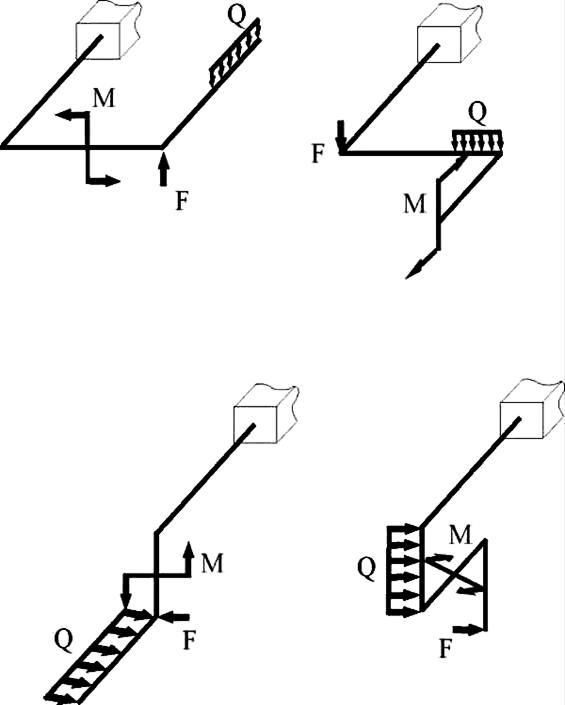
Рис.15

Пример 11. Рассмотрим ППС (рис.16,а). Прежде чем строить для этой системы эпюры M_x и M_кр, построим эпюры M_x и M_кр для каждой из четырех возможных нагрузок (они представлены на схеме), так как вообще говоря, любые эпюры M_x и M_кр в силу принципа независимости действия сил будут представлять собой алгебраическую сумму этих простейших эпюр, построенных от каждой нагрузки в отдельности, но, разумеется, с учетом места приложения нагрузок, их направлений и геометрической конфигурации системы.

Для достижения максимальной общности будем считать, что сила F, момент типа M₁ и момент типа M₂( имеется в виду плоскость действия каждого из них) приложены к концевому сечению (т.А на рис.16,а), а распределенная нагрузка приложена к первому от свободного конца участку стержня (стержень АВ на рис.16,а). Причем, все построения будем выполнять в общем виде, полагая, для наглядности, что a < l.

Пусть к плоско-пространственной системе (рис.16,в) приложена только сила F. Построим эпюры M_x,F и M_кр,F для заданной системы. Здесь, как и при любой другой внешней нагрузке, более сложным является построение эпюры изгибающих моментов M_x. В соответствии с ранее оговоренными принципами, для построения эпюры M_x в заданной ППС выделим 6 характерных сечений. Так как имеется жесткая заделка, то расчет ведем от свободного конца. При вычислении изгибающего момента очень важно правильно определить плоскость изгиба стержня, которому принадлежит рассматриваемое характерное сечение, т.к. плечо действующей нагрузки необходимо определить именно в плоскости изгиба.

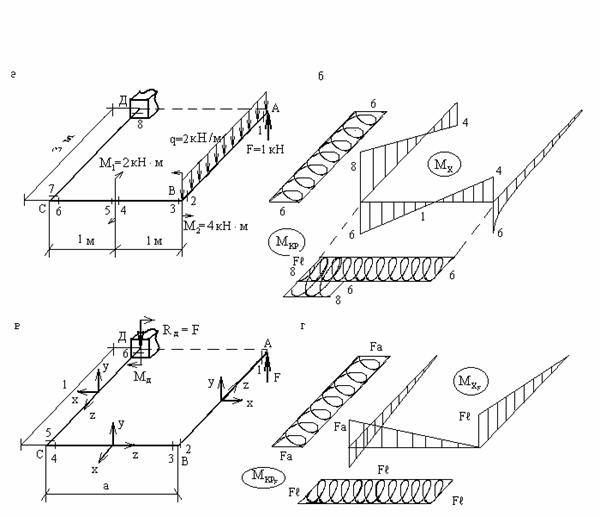
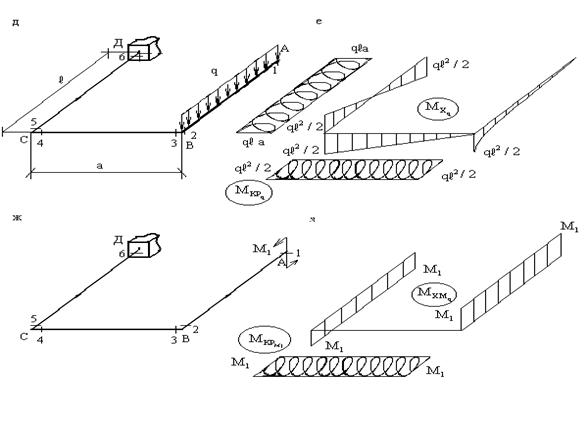
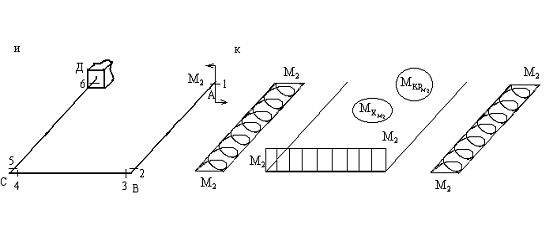
Рис.16

Стержень АВ изгибается в вертикальной плоскости, перпендикулярной плоскости чертежа;

M_x,1 = 0,

M_x,2 = F·l (сжаты верхние волокна).

Стержень ВС изгибается в вертикальной плоскости, параллельной плоскости чертежа:

M_x,3 = 0, (сила F не имеет плеча в плоскости изгиба!);

M_x,4 = F·a, (сжаты верхние волокна).

Стержень СД, как и стержень АВ, изгибается в вертикальной плоскости, перпендикулярной плоскости чертежа.

M_x,5 = F·l, (сжаты нижние волокна).

M_x,6 = 0 (сила F не имеет плеча в плоскости изгиба).

Остановимся подробнее на определении изгибающего момента M_x,5. Как видно из приведенных выше значений: M_x,5 = - M_x,2, то есть моменты в сечениях 2 и 5 (обратим внимание на их расположение, а не на нумерацию, которая, естественно, может быть совершенно произвольной) одинаковы по величине, но противоположны по направлению. Это утверждение можно доказать.

Причем, возможно как строгое доказательство, так и некоторые "нестрогие" рассуждения, приводящие к тому же факту. Начнем с последних. Под действием приложенной силы F (рис.16,в) происходит "перекос" системы: точка В смещается вверх, а точка С - вниз; при этом обе точки располагаются на одинаковом расстоянии (в вертикальной плоскости, перпендикулярной плоскости чертежа) от линии действия силы F, следовательно, моменты в сечениях 2 и 5 одинаковы, но противоположны по знаку.

Для иллюстрации другого подхода к "нестрогому" доказательству утверждения о том, что M_x,5 = - M_x,2, введем в рассмотрение так называемую скользящую систему координат (рис.16,в). Такое название связано с тем, что координатные оси как бы скользят вдоль ломаной продольной оси системы, не поворачиваясь вокруг нее. При этом на каждом участке плоско-пространственной системы ось z направлена вдоль продольной оси соответствующего стержня, ось y- вверх (или вниз) при расположении системы в горизонтальной плоскости, а ось x остается перпендикулярной к плоскости yoz. Как следует из чертежа, на участках АВ и СД ось x имеет противоположное направление, следовательно, моменты M_x имеют на этих участках разные знаки, а так как сечения 2 и 5 равноудалены от линии действия силы F, то очевидно равенство моментов в этих сечениях по абсолютной величине.

И, наконец, рассмотрим более строгое доказательство. Двигаясь от свободного конца при выборе отсеченной части, мы получили: M_x,2 = F·l (сжаты верхние волокна). Определим момент M_x в сечении 5, двигаясь при выборе отсеченной части со стороны жесткой заделки. Для определения момента таким способом необходимо знать реакции заделки. При действии на систему силы F из всех возможных в общем случае нагружения реакций в жесткой заделке возникают реакция R_D и опорный момент M_D, определяемые из условий равновесия:

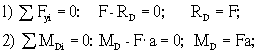
Теперь, двигаясь со стороны жесткой заделки, для сечения 5 получим:

M_x,5 = R_D · l = F · l (сжаты нижние волокна), то есть M_x,5 = - M_x,2 (момент M_D не влияет на величину M_x,5, так как его плоскость действия перпендикулярна плоскости изгиба).

Очевидно, что подобные рассуждения можно провести при любой внешней нагрузке, поэтому в дальнейшем при построении эпюры M_x всегда будем руководствоваться правилом: изгибающий момент в сечении 5 равен изгибающему моменту в сечении 2 (опять-таки, имеется в виду положение сечений, а не их порядковые номера) и противоположен ему по знаку, при условии, что на участке 2-5 не приложен сосредоточенный момент, который для сечения 5 является изгибающим, то есть момент типа M₁(рис.16,а). При наличии на участке 2-5 такого момента равенство ординат по модулю в сечениях 2 и 5 "искажается" на величину M₁ в соответствующую направлению M₁ сторону.

Теперь построим эпюру M_кр,F.

Участок АВ не подвержен кручению, так как сила F приложена к продольной оси стержня АВ. Участок ВС закручивается силой F с плечом l, следовательно:

M_кр,3 = M_кр,4 = F·l .

Участок СД также закручивается силой F, но с плечом a, то есть:

M_кр,5 = M_кр,6 = F·a.

Эпюры M_x,F и M_кр,F представлены на рис.16,г.

Аналогичным образом строятся эпюры изгибающих и крутящих моментов от распределенной нагрузки q (рис.16,д), сосредоточенного момента типа M₁(рис.16,ж) и сосредоточенного момента типа M₂(рис.16,и).

Не останавливаясь детально на построении этих эпюр, отметим некоторые особенности. Эпюра M_x на участке под распределенной нагрузкой ( и только на этом участке!)- квадратная парабола, направленная выпуклостью навстречу нагрузке. На участке СД - противоположном тому, где приложена нагрузка q - эпюра M_x пересекает ось в точке, расположенной напротив равнодействующей распределенной нагрузки (рис.16,д).

Анализ эпюр от сосредоточенных моментов M₁(рис.16,з) и M₂ (рис.16,к) позволяет сделать очевидный вывод о том, что если момент приводит к изгибу какого-либо стержня, то кручение на этом участке отсутствует и наоборот.

Теперь, учитывая накопленный опыт при построении эпюр от раздельного действия каждой из четырех нагрузок, рассмотрим более сложное нагружение (рис.16,а).

При указанных на этом рисунке нагрузках для построения эпюры M_x необходимо выделить 8 характерных сечений. Двигаясь от свободного конца, получим по участкам:

Участок АВ изгибается в вертикальной плоскости, перпендикулярной плоскости чертежа:

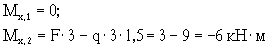
(сжаты нижние волокна).

Кручение на участке АВ отсутствует, так как сила F и нагрузка q имеют нулевые плечи относительно продольной оси участка АВ.

Участок ВС изгибается в вертикальной плоскости, параллельной плоскости чертежа.

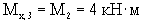(сжаты верхние волокна);

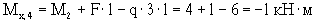(сжаты нижние волокна);

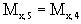, так как момент 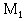, приложенный к отсеченной части для сечения 5, действует в плоскости, перпендикулярной ВС и на изгиб участка ВС не влияет;

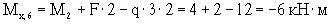(сжаты нижние волокна).

Для построения эпюры крутящих моментов на участке ВС рассмотрим отдельно участки 3-4 и 5-6, так как между сечениями 4 и 5 приложен момент M₁. Участок 3-4 закручивается силой F с плечом 3м и в противоположную сторону - нагрузкой q с плечом 1,5м:

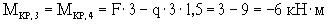(здесь знак "-" носит сугубо условный характер и может служить только для обозначения направления кручения). Участок 5-6 помимо силы F и нагрузки q закручивается еще и моментом M₁, причем, в том же направлении, что и нагрузкой q, поэтому:

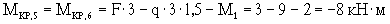
Участок 7-8 закручивается нагрузкой q с плечом 2м и в противоположную сторону - силой F с плечом 2м и моментом M₂, следовательно:

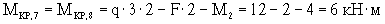
По вычисленным значениям строим эпюры M_x и M_кр(рис.16,б).