Частные случаи приведения системы сил.

Если пространственная система сил приводится к равнодейст­вующей, то момент равнодействующей относительно произвольной точки равен геометрической сумме моментов всех сил относительно той же точки. Пусть система сил имеет равнодействующую R и точка О лежит на линии действия этой равнодействующей. Если приводить заданную систему сил к этой точке, то получим, что главный момент равен нулю. Mo1=Mo+Mo1(Fo), т.к М₀ = 0. Частные случаи: 1.Гл.момент Lo=0; R¹0 – в этом случае система сил приводится к равнодействующей, причем R*=R. Если центр приведения лежит на линии действия силы R, то ситуация не изменится и сист.сил опять будет приводится к равнодействующей. 2.Пусть Lo¹0; R¹0. Покажем, что в этом случае сист.сил можно привести к равнодействующей. R=R₁=R₁’; [L_o] ~{R₁;R₁’}; {R₁;R₁’}~0; причем повернем эту пару сил так, чтобы R и R₁ лежали на одной прямой, тогда видим, что сист.сил {R₁;R₁’}~0 {R;L_o}~ {R=R₁=R₁’}~{R₁’}. D=L_o/R. (27продолжение)3.Пусть R=0, L_o¹0. В этом случае система сил приводится к паре. Причем вне зависимости от вцыбора центра приведения система сил будет приводится к одной и той же паре сил с моментом L_o. Т.к.главный вектор не зависит от выбора центра приведения.

Приведение системы сил к динаме ( динамическому винту).

В общем случае для произвольной системы сил главный вектор и главный момент составляют между собой некоторый угол. Главный момент M_O разложим на две составляющие, одну из них мы обозначим M_O' и направим по главному вектору, а вторую - M_O'' - направим перпендикулярно первой (рис. 27, a).

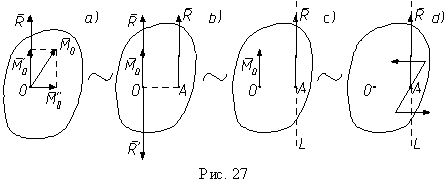
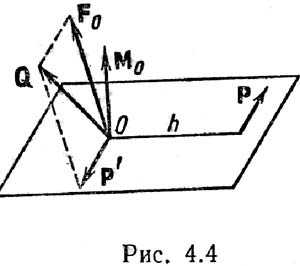Вторую составляющую представим в виде пары, одной из сил которой уравновесим главный вектор (рис. 27, b). Таким образом, система сил приведена к одной силе (по величине и направлению равной главному вектору) и к одной перпендикулярной ей паре с моментом M_O', параллельным силе, равным по величине проекции главного момента на главный вектор (рис. 27, c и d). Такую совокупность силы и пары сил называют динамическим винтом, а линию действия AL силы в динамическом винте называют центральной осью системы сил. Первая составляющая главного момента M_O' не зависит от выбора центра приведения. При выборе нового центра приведения, например O₁, сила в динамическом винте не изменится (главный вектор является первым инвариантом системы сил) и M_O1' = M_O', то есть эта составляющая или проекция главного момента на главный вектор являются вторым инвариантом системы сил.

Уравнение центральной винтовой оси системы.

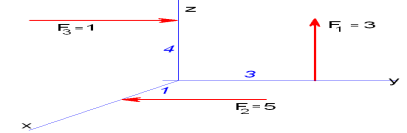
Этот вопрос рассмотрен на примере задачи.

Главный вектор:
R_x=0, R_y=F₂ +F₃ = 4, R_z=F₁ = 3, R=5.

Главный момент:
M_x=F₁·3  F₃·4 = 94=5, M_y=0, M_z = F₂·1 = 5, M=52.

Инвариант : I=M_xR_x+M_yR_y+M_zR_z = -15

Минимальный момент : M^*= I/R = -15/5 = -3

Шаг винта : p=I/R² = M^*/R = -3/5 = -0.6

Уравнения центральной винтовой оси
M_x - yR_z + zR_y = pR_x,
M_y - zR_x + xR_z = pR_y,
M_z - xR_y + yR_x = pR_z, имеют вид 5-3y-4z=0, 3x-2.4=0, -3.2+4x=0.
Точка пересечения центральной винтовой оси с плоскостью z=0, x=0.8, y=5/3