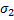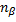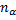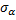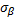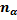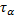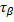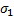Эпюры внутренних усилий и порядок их построения.

Содержание и задачи курса СМ. История развития науки о прочности и ее связь с другими науками. Причины разрушения конструкций.

СМ – учебная дисциплина, в которой изучаются практические методы расчета на прочность, жесткость и устойчивость с учетом долговечности и экономичности.

Основные положения СМ опираются на законы и теоремы общей механики и в первую очередь ста­тики, но в отличие от тео­ретической механики, которая базируется на гипотезе об абсолютно твер­дом теле, в СМ рассматриваются деформируемые тела.

Прочность – способность конструкций не разрушаться под действием внешних сил.

Жесткость – способность конструкций со­противляться деформированию под действием внешних сил.

Устойчивость – способность конструкций сохранять форму под нагрузкой.

Долговечность – свойство объекта сохранять работоспособное со­стояние при установленной системе технического обслуживания и ремонта.

Проведение расчетов на прочность, жесткость, устойчивость, долго­вечность, как правило, осуществляется на стадии проектирования конст­рукций и сооружений. Основные задачи сводятся:

1) к установлению оптимальных размеров и форм элементов конст­рукций;

2) к выбору конструкционных материалов, обеспечивающих надеж­ность конструкции.

Гук заключил: «Каково удлинение, такова и сила», или в современной трактовке: «Деформация пропорциональна нагрузке». Но в начале 19 в. наука о прочности приобретает теоретический характер. Эйлер занимался расчетом сжатых стержней на устойчивость. Журавский получил формулу для определе­ния касательных напряжений при изгибе, которой пользуются и в настоящее время.

СМ не является обособленной наукой, она тесно связана с общей механикой, математикой, физикой твердого тела, материа­ловедением и технологией металлов.

Основные причины разрушения конструкций:

- ошибки, допущенные в проектах ;

- несоответствие примененной марки стали характеру нагружения и температурным условиям ;

- дефекты заводского изготовления конструкций;

- нарушение при эксплуатации конструкций расчетных схем, установленных для элементов, и превышение допустимых нагрузок

- несовершенство действующих норм и правил проектирования и изготовления металлоконструкций

- другие причины .

3) Внутренние силы и их природа. Метод сечений и его сущность, порядок действий. Название внутренних усилий и их выражение, формулировка для каждого усилия. Виды нагруженний (сопротивлений бруса).

Внутренние силы – силы взаимодействия между

частичками данного тела, обеспечивающие целостность тела.

Метод сечений:

1) рассекают брус воображаемой плоскостью на две части;

2) отбрасывают мысленно одну из частей;

3) заменяют влияние отброшенной части на оставленную внутренними усилиями;

4) уравновешивают, составляют уравнения равновесия для системы сил которая действует на оставленную часть.

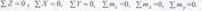
продольная сила N численно равна алгебраической сумме проек­ций всех внешних сил, действующих на одну из частей рассеченно­го бруса, на продольную ось z;

Qx - то же на ось х; Qy - то же на ось у;

крутящий момент Мz численно равен алгебраической сумме моментов всех внешних сил, действующих на одну из частей относительно оси бруса z;

Мх - то же относительно оси х;

Му - то же относительно оси у.

Метод сечений позволяет найти все внутренние усилия и моменты в любом сечении бруса при действии любой нагрузки.

Каждому из внутренних усилий соответствует простой вид сопротив­ления (нагружения) бруса. Продольной силе N - растяжение или сжатие, поперечной силе Qx или Qy - сдвиг, крутящему моменту Mz - кручение, а изгибающим моментам Мх Му - изгиб.

Понятие о прочности конструкции. От чего она зависит. Опасные напряжения. Понятие потери несущей способности конструкции. Идея условия прочности. Методы расчетов на прочность и области их применения. Три типа задач на прочность. Порядок расчета на прочность.

Прочность – способность конструкции не разрушаться под действием нагрузок.

Прочность зависит от напряжения Напряжения называются опасными (предельными) если они вызывают у конструкции потерю несущей способности т. е. вызывают разрушение или большие деформации.

Для пластичных материалов:

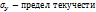
Для хрупких:

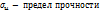
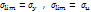
От эксплуатационных нагрузок не должно превышать: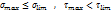

Основные задачи расчетов на прочность:

Проверочный расчет (проверка прочности)

Проектировочный расчет (размеры)

Определение несущей способности конструкции (определение допускаемой нагрузки)

Для решения этих задач разработано три метода расчетов:

Расчет по допускаемым напряжениям;

Расчет по разрушающим (предельным) нагрузкам;

Расчет по предельным состояниям.

потеря несущей спо­собности конструкции, т. е. разрушение или возникновение больших де­формаций.

Расчет по предельным состояниям. Понятие и критерий предельного состояния конструкции (сооружения). СНиП. Две группы предельных состояний и расчеты на прочность и жесткость. Коэффициенты, учитывающие отклонения различных факторов от нормативных значений. Нормативная и расчетная нагрузка. Нормативное и расчетное сопротивление материала. Условие прочности (идея). Условие прочности при растяжении и сжатии. Пример расчета. Область применения этого метода.

Моментов.

Пусть требуется найти положение главных центральных осей и вычислить относительно них моменты инерции для плоского сечения, состоящего из швеллера и полосы (рис. 6.13):

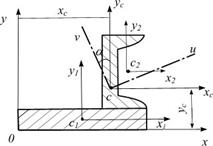
Рис. 6.13

Проводят произвольную систему координат xOy.

Разбивают сечение на простые фигуры и по формулам (6.5) определяют положение центра тяжести С.

Находят моменты инерции простых фигур относительно собственных центральных осей, используя сортамент или по формулам.

Через точку С проводят центральные оси x_c и y_c параллельно осям простых фигур.

Определяют моменты инерции простых фигур относительно центральных осей сечения, используя формулы параллельного переноса (6.13).

Определяют центральные моменты инерции всего сечения как сумму соответствующих моментов простых фигур, найденных в пункте 5.

Вычисляют угол 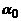по формуле (6.26) и, поворачивая оси x_c и y_c на угол 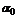, изображают главные оси u и v.

По формулам (6.29) вычисляют 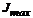и .

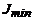Делают проверку:

а) ;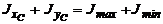

б) 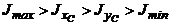, если ;

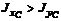в) .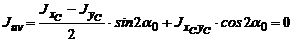

36) Общий прядок определения главных центральных моментов инерции. Пример:

1. Если фигура имеет две оси симметрии, то эти оси и будут ГЦО.

2. Для правельных фигур ( у которых больше 2- х оссей) все оси будут главными

3. Проводим вспомогательные оси(Х’ O’ Y’)

4. Разбиваем данное сечение на простые фигуры и показываем их собственные ЦО.

5. Находим положение ГЦО по формуле(21)

6. Вычисляем значения ГЦМ по формуле (23)

· Imax + Imin = Ix + Iy

· Imax >Ix>Iy>Iminесли Ix>Iy

· Iuv = Ix-Iy/2 sin2a + Ixycos2a +0

Формула 21:Tg2a = - 2Ixy/Ix - Iy

Формула23: Imax, Imin = *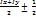

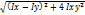
37) Изгиб. Классификация видов изгиба. Прямой и чистый изгиб. Картина деформирования балки. Нейтральный слой и ось. Основные допущения.

Изгиб – деформирование при котором в поперечном сечении возникает изгибающий момент Мх. Брус, который работает на изгиб-балка

Виды изгиба:

Чистый изгиб имеет место, если в сечении возникает только изгибающий момент

Поперечный изгиб- если одновременно с моментом возникает поперечная сила

Плоский - все нагрузки лежат в одной плоскости

Пространственный - если все нагрузки лежат в разных продольных плоскостях

Прямой - если силовая плоскость совпадает с одной из главных осей инерции

Косой - если силовая плоскость не совпадает ни с одной из главных осей

В результате деформирования на участке чистого изгиба можно видеть:

- продольные волокна искривляются по дуге окружности: одни- укорачиваются, другие-удлиняются; между ними есть слой волокон, которые не меняют своей длины- нейтральный слой (н.с.), линию его пересечения с плоскостью поперечного сечения называют нейтральной осью (н.о.)

-расстояние между продольными волокнами не меняется

-поперечные сечения, оставаясь прямыми, поворачиваются на некоторый угол

Допущения:

1.Оненадавливании продольных волокон друг на друга, т.е. каждое волокно находиться в состоянии простого растяжения или сжатия, что сопровождается возникновением нормальных напряжений Ϭ

2.О справедливости гипотезы Бернули, т.е. сечения балки, плоские и нормальные к оси до деформации, остаются плоскими и нормальными к ее оси после деформации

Перемещение при изгибе (линейные и угловые). Точное и приближенное уравнение упругой линии балки. Определение перемещения методом непосредственного интегрирования. Пример.

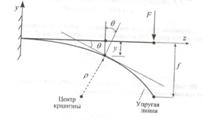
Линейные перемещения-прогибы у - направлены перпендикулярно продольной оси z балки. Наибольший прогиб - стрела прогиба f.

Угол между новым и старым положением сечения - угол поворота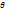

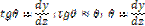
Точное уравнение упругой линии балки:

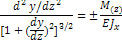
Приближенное уравнение упругой линии балки:

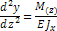
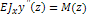
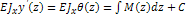- уравнение углов поворота

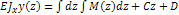- уравнение прогибов

Метод Непосредственного интегрирования

Разбивают балку на участки и для каждого записывают выражение изгибающего момента Mz

Для каждого участка составляют диф. уравнение, подставляя Mz

Для каждого участка диф. ур-е дважды интегрируют и получают общие выражения для угла поворота 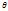и прогиба у

Из условий на опорах балки и на границах участков определяют постоянные интегрирования C и D и подставляют в уравнения

Определяют 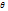и у в нужном сечении, подставляя значения z

Пример. Определить наибольший угол поворота и стрелу прогиба.

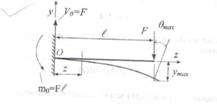
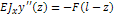
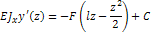
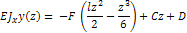
При z=0 угол поворота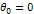

При z=0 прогиб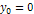

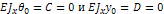
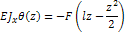
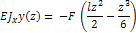
Полагая что z=l

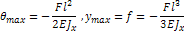
Знак «минус» указывает на то, что поворот по часовой стрелке и что конец опускается вниз.

Метод начальных параметров. Вывод универсального уравнения при изгибе. Начальные параметры. Порядок (алгоритм) вычисления перемещений методом начальных параметров. Пример. Условие жесткости при изгибе.

Выбираем единое начало координат на левом конце балки

Если распределенная нагрузка не доходит до правого конца, продлеваем ее и показываем компенсирующую

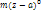,если на балку действует момент, где а - абсцисса до точки приложения силы

Интегрирование вести без раскрытия скобок

+

+

+

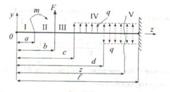
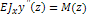
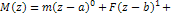
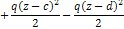
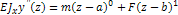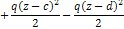
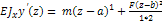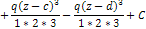
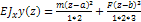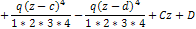
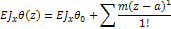
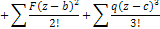
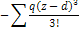
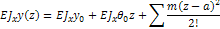
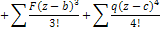
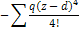
Начало координат совпадает с заделкой. Начальные параметры 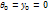(рис)

Начало координат совпадает с шарнирной опорой

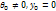
Начало координат находится на свободном конце

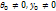
Находим из граничных условий

Порядок расчета:

Определяем опорные реакции и проставляем на расчетной схеме

Выбираем единое начало координат на левом конце балки и выявляем равны 0 начальные параметры или нет

Если нагрузка q не доходит до правого конца ее продлевают и показывают компенсирующую

Записываем универсальное уравнение прогиба обычно для последнего участка, учитывая силы расположенные левее рассматриваемого сечения, слагаемые имеют знак изгибающего момента

Дифференцируем уравнение и получаем формулу угла поворота

Если начальные параметры не равны 0 то их определяем из граничных условий

Подставляем в уравнения соответствующие значения z, определяем прогиб и угол поворота

Условие жесткости: наибольший прогиб не должен превышать предельно допустимого, устанавливаемого СНиПом.

;

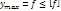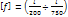
Потенциальная энергия.

Работа затрачиваемая на кручение в пределах упругих дфрм, равна кол-ву потенциальной энергии, накопленной в брусе, и вычисляется как площадь треугольника на диаграмме кручения.

Mu

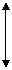
Mz

U

Теория напряженного состояния в точке. Полное напряжение в точке на площадке. Объект исследования. Тензор напряжений. Главные площадки и главные напряжения. Классификация напряженных состояний и соответствующие им виды нагружений.

Напряженное состояниев данной точке-совокупность σ и τ, действующих по различным площадкам, проходящим через данную точку.

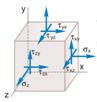
Н.с. в точке характерезуется тремя компонентами, а в (.) тела 9 компонентами.

Площадки на которых τ=0 назыв главными,а σ-глав напряж, обладают св-вом экстремальности σ1>σ2>σ3.

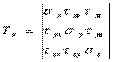Совокупность напряжений полностью характеризует напряжённое состояние частицы тела. Эту совокупность записывают в виде квадратной матрицы и называют тензором напряжений Коши.

Линейное н.с.-имеет место если напряж действ на пл-дках по одному направ(два других свободны от напряж).При растяж и сжат, в некторых (.) стержня работающего на изгиб или сложное сопротивление.

Классификация Н.с.

	Плоское н.с.- при котором напряж действует по двум направлениям, а третье свободно.При круч,сдвиг,изгиб,сложном спротив.

Объемное н.с.-по всем направлениям действ напряж. Возникает в мат-ле дорожного покрытияв месте давления колес на плиту покрытия, в месте контакта колес с рельсами.

Прямая задача.

По известным данным пл-док действ на них глав напряж определить τ и σ,действ на пл-ках α и β.

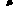
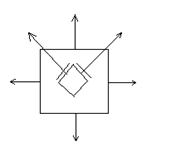
P-полюс Мора.

Частный случай.

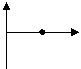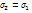
Круг Мора вырождается в (.) все пл-ки будут глав.

55. Плоское напряженное состояние. Решение обратной задачи с помощью круга Мора: по известным напряжениям, действующим на двух взаимно перпендикулярных площадках, найти главные напряжения и главные площадки (графически и аналитически). Частные случаи. Плоское н.с.- при котором напряж действует по двум направлениям, а третье свободно.При круч,сдвиг,изгиб,сложном спротив.

α

β

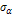=σ₁ cos²α+ 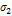sin²α

α=45

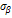=σ₂ cos²α+ 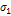sin²α аналитич.

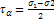sin2α ^{реш.прям.задачи}

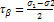sin2α

1) при п.н.с. есть закон парности: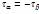

2)сумма σ на двух взаимно перпенедекуляр пл-дках является постоянной и =сумме главных напряж: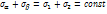

3)м/у теорией моментов инерции и теории напряж существует полная аналогия.

Моменты инерции	Т. напряж
Ix,Iy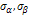
Ixy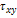
Imax,Imin	σ1>σ2>σ3

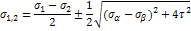
4)положение глав пл-док определяют :

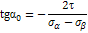
Круг Мора-геометрич место точек, ординаты и абсциссы которых соответст σ и τ. возникающие на данной пл-дке.

Полюс круга Мора-это (.) на круге Мора который пересекает лучи паралелль нормалям по всем пл-дкам данной серии.

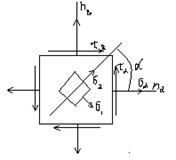
Обратная задача.

По известным пл-кам под углом α и β и τ и σ,найти σ₁ и σ_2.

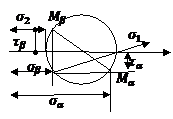
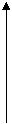Частный случай. чистый сдвиг.

Напряжения в наклонныхсечениях стержня при растяжении и сжатии. Вывод формул и анализ. Наибольшие касательные напряжения. Доказать закон парности касательных напряжений. Напряженное состояние в точке.

Как определяются напряжения в поперечных и наклонных сечениях бруса?

Р– сила, равная произведению напряжения 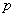на площадь наклонного сечения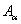

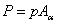
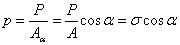
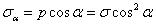
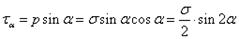
®Наибольшие касательные напряжения возникают при угле 45 градусов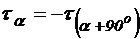

®З. парности касат. Напряжений.(на двух взаимно перпендикулярных площадках возникают одинаковые по модулю и разные по направлению касательные напряжения)

Напряжённое состояние в точке

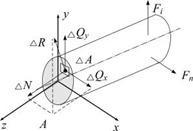
Отношение 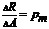представляет собой среднее напряжение на площадке 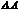. В пределе получаем

,

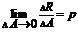
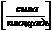где 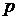–полное напряжение в точке K площади ΔА.

В системе СИ напряжение выражается в паскалях Па=н/м² или мегапаскаляхМПа=10⁶ Па.

Разложим вектор 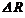по осям координат на составляющие 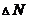, , 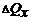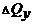и запишем выражения:

, , ,

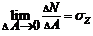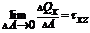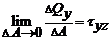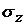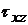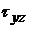где –нормальное напряжение; и –касательные напряжения.

Тогда напряжение 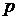можно рассматривать какполное напряжениевточке на данной площадке:

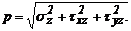
Растяжение и сжатие. Относительная продольная деформации. Вывод формулы для абсолютной деформации (формулы жесткости). Жесткость сечения. вычисление полного удлинения бруса и удлинение, связанное с температурным воздействием.

Растяжение и сжатие -вид нагружения бруса, при котором внутренние силы в поперечном сечении приводятся только к продольной силе N.

Продольная деформация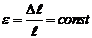

Формула жёсткости для абсолютной деформаци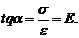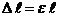и

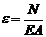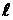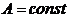и .Тогда абсолютное удлинение участка стержня длиной при и 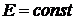будет равно

,

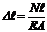EA -жесткостьстержня при растяжении ,сжатии

Вычесление полного удлинения бруса ,удлинение связанное с температурным воздействием-Если на участке 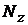и 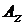переменны (рис. 3.9 б), то полное удлинение участка 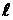получим, суммируя удлинения бесконечно малых участков dz:

.

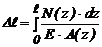Для бруса, имеющего несколько участков:

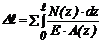. (3.14)

Удлинение, связанное с температурным воздействием:

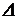
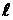_t^o 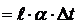, (3.15)

где 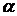– коэффициент температурного расширения материала; 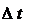– изменение температуры.

14)растяжение и сжатие. Абсолютная и относительная поперечная деформация. Связь между продольной и поперечной деформациями. Коэффициент Пуассона, его физический смысл и способы определения

Абсолютная и относительная поперечная деформация -Абсолютная поперечная деформация определяется как разность размеров после деформации и до нее:

; .

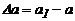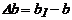Относительная поперечная деформация для изотропных материалов по всем направлениям одинакова:

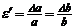
Связь между продольной и поперечной деформациями,коэфпуассона ,его физ и способы определения 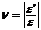или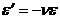

где 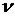– коэффициент поперечной деформации (коэффициент Пуассона) – безразмерная величина, упругая постоянная материала, определяемая экспериментально. Для всех изотропных материалов 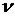= 0 ¸ 0,5. Для пробки 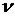»0; для каучука 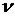» 0,5; для стали 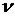» 0,3.

15.Перемещение поперечного сечения при растяжении и сжатии. Дифференцальная зависимость между перемещением 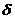и продольной силой N. Построение эпюры перемещений(пример). Условие жесткости.

Перемещение поперечного сечения при растяжении сжатии 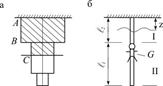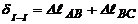(под буквой а )

Диференциальная зависимость м/у перемещением и продольной силой .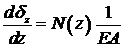

Пример построения эпюры-Эпюру перемещений начинают строить от защемленного конца, вычисляя перемещения характерных сечений

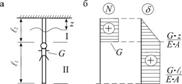
Рис. 3.11

I участок,0<z< 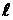₁: 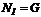;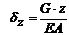(линейный закон), при 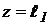перемещение .

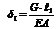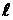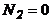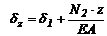II участок,0<z< ₂: , ;или 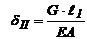(const).

Для обеспечения нормальной работы конструкций размеры их элементов необходимо выбирать так, чтобы выполнялось условие жесткости,которое состоит в ограничении упругих перемещений:

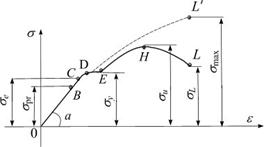
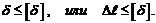(3.19)

где 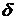и 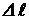– наибольшее перемещение; 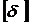–допускаемое перемещение.

Содержание и задачи курса СМ. История развития науки о прочности и ее связь с другими науками. Причины разрушения конструкций.

СМ – учебная дисциплина, в которой изучаются практические методы расчета на прочность, жесткость и устойчивость с учетом долговечности и экономичности.

Основные положения СМ опираются на законы и теоремы общей механики и в первую очередь ста­тики, но в отличие от тео­ретической механики, которая базируется на гипотезе об абсолютно твер­дом теле, в СМ рассматриваются деформируемые тела.

Прочность – способность конструкций не разрушаться под действием внешних сил.

Жесткость – способность конструкций со­противляться деформированию под действием внешних сил.

Устойчивость – способность конструкций сохранять форму под нагрузкой.

Долговечность – свойство объекта сохранять работоспособное со­стояние при установленной системе технического обслуживания и ремонта.

Проведение расчетов на прочность, жесткость, устойчивость, долго­вечность, как правило, осуществляется на стадии проектирования конст­рукций и сооружений. Основные задачи сводятся:

1) к установлению оптимальных размеров и форм элементов конст­рукций;

2) к выбору конструкционных материалов, обеспечивающих надеж­ность конструкции.

Гук заключил: «Каково удлинение, такова и сила», или в современной трактовке: «Деформация пропорциональна нагрузке». Но в начале 19 в. наука о прочности приобретает теоретический характер. Эйлер занимался расчетом сжатых стержней на устойчивость. Журавский получил формулу для определе­ния касательных напряжений при изгибе, которой пользуются и в настоящее время.

СМ не является обособленной наукой, она тесно связана с общей механикой, математикой, физикой твердого тела, материа­ловедением и технологией металлов.

Основные причины разрушения конструкций:

- ошибки, допущенные в проектах ;

- несоответствие примененной марки стали характеру нагружения и температурным условиям ;

- дефекты заводского изготовления конструкций;

- нарушение при эксплуатации конструкций расчетных схем, установленных для элементов, и превышение допустимых нагрузок

- несовершенство действующих норм и правил проектирования и изготовления металлоконструкций

- другие причины .

3) Внутренние силы и их природа. Метод сечений и его сущность, порядок действий. Название внутренних усилий и их выражение, формулировка для каждого усилия. Виды нагруженний (сопротивлений бруса).

Внутренние силы – силы взаимодействия между

частичками данного тела, обеспечивающие целостность тела.

Метод сечений:

1) рассекают брус воображаемой плоскостью на две части;

2) отбрасывают мысленно одну из частей;

3) заменяют влияние отброшенной части на оставленную внутренними усилиями;

4) уравновешивают, составляют уравнения равновесия для системы сил которая действует на оставленную часть.

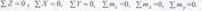
продольная сила N численно равна алгебраической сумме проек­ций всех внешних сил, действующих на одну из частей рассеченно­го бруса, на продольную ось z;

Qx - то же на ось х; Qy - то же на ось у;

крутящий момент Мz численно равен алгебраической сумме моментов всех внешних сил, действующих на одну из частей относительно оси бруса z;

Мх - то же относительно оси х;

Му - то же относительно оси у.

Метод сечений позволяет найти все внутренние усилия и моменты в любом сечении бруса при действии любой нагрузки.

Каждому из внутренних усилий соответствует простой вид сопротив­ления (нагружения) бруса. Продольной силе N - растяжение или сжатие, поперечной силе Qx или Qy - сдвиг, крутящему моменту Mz - кручение, а изгибающим моментам Мх Му - изгиб.

Эпюры внутренних усилий и порядок их построения.

Графики, показывающие изменение внутренних усилий по длине бруса при постоянном положении нагрузок, называются эпюрами.

Порядок построения эпюр:

1. Находят все внешние силы, действующие на брус (активные и ре­активные).

2. Разбивают брус на участки, в пределах которых внутренние усилия изменяются по одной закономерности.

Участком называется часть стержня между сосредоточенными нагруз­ками М, F или часть стержня, в пределах которого распределенная нагрузка q меняется по одному закону.

3. На каждом участке проводят произвольное сечение и фиксируют его абсциссой z.

4. Применяя метод сечений, для каждого участка составляют выра­жения для внутренних усилий.

5. Меняя значение z, находят внутренние усилия на границах участков и в характерных сечениях.

6. Параллельно оси бруса проводят ось (базу), на которой строят эпюру.

7. Ординаты эпюры в определенном масштабе откладывают от оси по перпендикуляру и проставляют значения характерных ординат.

8. В поле эпюры ставят знак усилия и наносят штриховку линиями, перпендикулярными к базе.

Эпюры внутренних усилий, как правило, строят для того, чтобы вы­явить опасные сечения, т.е. сечения, в которых существует большая ве­роятность разрушения из-за того, что там внутренние усилия достигают наибольших значений