Эпюры внутренних усилий при растяжении-сжатии

ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ ПРИ РАСТЯЖЕНИИ-СЖАТИИ

Растяжением или сжатием называется такой простой вид сопротивления, при котором внешние силы приложены вдоль продольной оси бруса, а в поперечном сечении его возникает только нормальная сила.

Рассмотрим расчетную схему бруса постоянного поперечного сечения с заданной внешней сосредоточенной нагрузкой Р и распределенной q, (рис.1).

а) расчетная схема, б) первый участок, левая отсеченная часть, в) второй участок, левая отсеченная часть, г) второй участок, правая отсеченная часть, д) эпюра нормальных сил

Рис.1. Построение эпюры нормальных сил:

Пусть 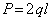. Прежде всего определим опорную реакцию R, задавшись ее направлением вдоль оси х.

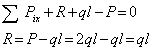
Брус имеет 2 участка 1 и 2.

В пределах первого участка мысленно рассечем брус на 2 части нормальным сечением и рассмотрим равновесие, допустим левой части, введя следующую координату х₁, рис.1 б:

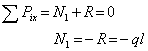
Следовательно, в пределах первого участка брус претерпевает сжатие постоянной нормальной силой.

Аналогично поступим со вторым участком. Мысленно рассечем его сечением 2—2, и рассмотрим равновесие левой части (рис.1 в).Установим предварительно границы изменения х₂:

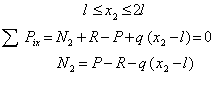
Подставляя граничные значения параметра х₂, получим:

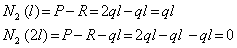
Таким образом, в пределах второго участка брус растянут и нормальная сила изменяется по линейному закону.

Аналогичный результат получается и при рассмотрении правой отсеченной части (рис.1 г):

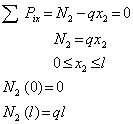
На основе полученных данных строится эпюра нормальных сил в виде графика распределения нормальной силы по длине бруса (рис.1 д). Характерно, что скачки на эпюре обусловлены наличием в соответствующих сечениях сосредоточенных сил R и Р, что в свою очередь может служить правилом правильности выполненных построений.

ТЕНЗОР ДЕФОРМАЦИИ

Рассмотрим вначале случай плоской деформации (рис. 4). Пусть плоский элемент MNPQ перемещается в пределах плоскости и деформируется (изменяет форму и размеры). Координаты точек элемента до и после деформации отмечены на рисунке.

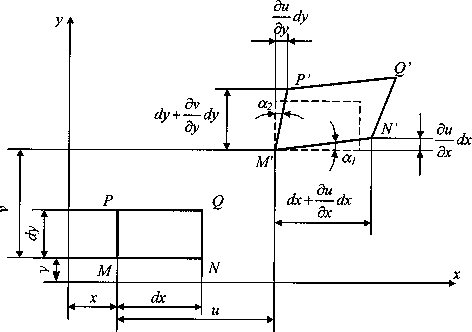
Рис.4. Плоская деформация.

По определению относительная линейная деформация в точке М в направлении оси Ох равна

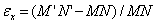
Из рис. 4 следует

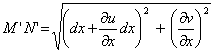
Учитывая, что MN=dx, получим

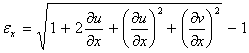
В случае малых деформаций, когда 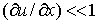, , 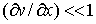можно пренебречь квадратичными слагаемыми. С учетом приближенного соотношения

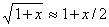
справедливого при x<<1, окончательно для малой деформации получим

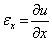
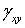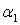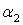Угловая деформация определяется как сумма углов и (4). В случае малых деформаций

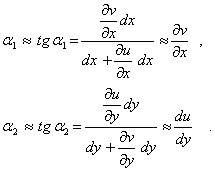
Для угловой деформации 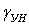имеем

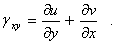
Проводя аналогичные выкладки в общем случае трехмерной деформации, имеем девять соотношений

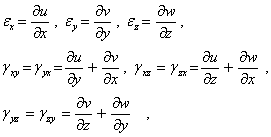(6)

связывающих линейные и угловые деформации с перемещениями. Эти соотношения носят название соотношений Коши.

Три линейных и шесть угловых деформаций (6) образуют тензор малых деформаций

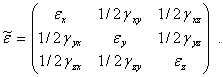(7)

Этот тензор полностью определяет деформированное состояние твердого тела. Он обладает теми же свойствами, что и тензор напряжений. Свойство симметрии непосредственно следует из определения угловых деформаций. Главные значения и главные направления, а также экстремальные значения угловых деформаций и соответствующие им направления находятся теми же методами, что и для тензора напряжений.

Инварианты тензора деформаций определяются аналогичными формулами, причем первый инвариант тензора малых деформаций имеет ясный физический смысл. До деформации его объем равен dV₀ =dxdydz. Если пренебречь деформациями сдвига, которые изменяют форму, а не объем, то после деформации ребра будут иметь размеры

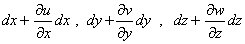
(рис. 4), а его объем будет равен

.

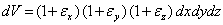Относительное изменение объема

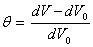
в пределах малых деформаций составит

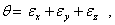
что совпадает с определением первого инварианта. Очевидно, что изменение объема есть физическая величина, не зависящая от выбора системы координат.

Так же, как и тензор напряжений, тензор деформаций можно разложить на шаровой тензор и девиатор. При этом первый инвариант девиатора равен нулю, т. е. девиатор характеризует деформацию тела без изменения его объема.

Лекция № 8. Упругость и пластичность. Закон Гука

Действие внешних сил на твердое тело приводит к возникновению в точках его объема напряжений и деформаций. При этом напряженное состояние в точке, связь между напряжениями на различных площадках, проходящих через эту точку, определяются уравнениями статики и не зависят от физических свойств материала. Деформированное состояние, связь между перемещениями и деформациями устанавливаются с привлечением геометрических или кинематических соображений и также не зависят от свойств материала. Для того чтобы установить связь между напряжениями и деформациями, необходимо учитывать реальные свойства материала и условия нагружения. Математические модели, описывающие соотношения между напряжениями и деформациями, разрабатываются на основе экспериментальных данных. Эти модели должны с достаточной степенью точности отражать реальные свойства материалов и условия нагружения.

Наиболее распространенными для конструкционных материалов являются модели упругости и пластичности. Упругость — это свойство тела изменять форму и размеры под действием внешних нагрузок и восстанавливать исходную конфигурацию при снятии нагрузок. Математически свойство упругости выражается в установлении взаимно однозначной функциональной зависимости между.компонентами тензора напряжений и тензора деформаций. Свойство упругости отражает не только свойства материалов, но и условия нагружения. Для большинства конструкционных материалов свойство упругости проявляется при умеренных значениях внешних сил, приводящих к малым деформациям, и при малых скоростях нагружения, когда потери энергии за счет температурных эффектов пренебрежимо малы. Материал называется линейно-упругим, если компоненты тензора напряжений и тензора деформаций связаны линейными соотношениями.

При высоких уровнях нагружения, когда в теле возникают значительные деформации, материал частично теряет упругие свойства: при разгрузке его первоначальные размеры и форма полностью не восстанавливаются, а при полном снятии внешних нагрузок фиксируются остаточные деформации. В этом случае зависимость между напряжениями и деформациями перестает быть однозначной. Это свойство материала называется пластичностью. Накапливаемые в процессе пластического деформирования остаточные деформации называются пластическими.

Высокий уровень нагружения может вызвать разрушение, т. е. разделение тела на части. Твердые тела, выполненные из различных материалов, разрушаются при разной величине деформации. Разрушение носит хрупкий характер при малых деформациях и происходит, как правило, без заметных пластических деформаций. Такое разрушение характерно для чугуна, легированных сталей, бетона, стекла, керамики и некоторых других конструкционных материалов. Для малоуглеродистых сталей, цветных металлов, пластмасс характерен пластический тип разрушения при наличии значительных остаточных деформаций. Однако подразделение материалов по характеру разрушения на хрупкие и пластичные весьма условно, оно обычно относится к некоторым стандартным условиям эксплуатации. Один и тот же материал может вести себя в зависимости от условий (температура, характер нагружены я, технология изготовления и др.) как хрупкий или как пластичный. Например, пластичные при нормальной температуре материалы разрушаются как хрупкие при низких температурах. Поэтому правильнее говорить не о хрупких и пластичных материалах, а о хрупком или пластическом состоянии материала.

Пусть материал является линейно-упругим и изотропным. Рассмотрим элементарный объем, находящийся в условиях одноосного напряженного состояния (рис. 1), так что тензор напряжений имеет вид

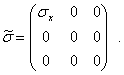
При таком нагружении происходит увеличение размеров в направлении оси Ох, характеризуемое линейной деформацией 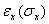, которая пропорциональна величине напряжения

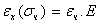(1)

Рис.1. Одноосное напряженное состояние

Это соотношение является математической записью закона Гука, устанавливающего пропорциональную зависимость между напряжением и соответствующей линейной деформацией при одноосном напряженном состоянии. Коэффициент пропорциональности E называется модулем продольной упругости или модулем Юнга. Он имеет размерность напряжений.

Наряду с увеличением размеров в направлении действия; же напряжения 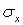происходит уменьшение размеров в двух ортогональных направлениях (рис. 1). Соответствующие деформации обозначим через 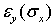и 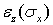, причем эти деформации отрицательны при положительных 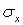и пропорциональны :

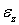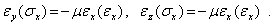(2)

Коэффициент пропорциональности 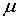называется коэффициентом Пуассона, который в силу изотропности материала одинаков для обоих ортогональных направлений.

Соотношения, аналогичные (1) и (2), в случае одноосного нагружения в направлении осей Оу, Ог напряжением 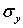, , 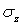соответственно имеют вид

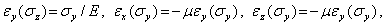	(3)
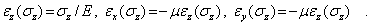	(4)

При одновременном действии напряжений по трем ортогональным осям, когда отсутствуют касательные напряжения, для линейно-упругого материала справедлив принцип суперпозиции (наложения решений):

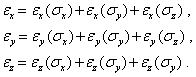
С учетом формул (1 — 4) получим

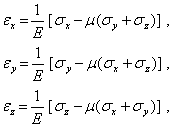(5)

Касательные напряжения вызывают угловые деформации, причем при малых деформациях они не влияют на изменение линейных размеров, и следовательно, на линейные деформации. Поэтому они справедливы также в случае произвольного напряженного состояния и выражают так называемый обобщенный закон Гука.

Угловая деформация 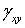обусловлена касательным напряжением 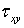, а деформаци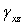и и 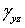— соответственно напряжениям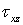и и 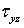. Между соответствующими касательными напряжениями и угловыми деформациями для линейно-упругого изотропного тела существуют пропорциональные зависимости

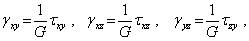(6)

которые выражают закон Гука при сдвиге. Коэффициент пропорциональности G называется модулем сдвига. Существенно, что нормальное напряжение не влияет на угловые деформации, так как при этом изменяются только линейные размеры отрезков, а не углы между ними (рис. 1).

Линейная зависимость существует также между средним напряжением (2.18), пропорциональным первому инварианту тензора напряжений, и объемной деформацией (2.32), совпадающей с первым инвариантом тензора деформаций:

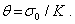(7)

Рис.2. Плоская деформация сдвига

Соответствующий коэффициент пропорциональности К называется объемным модулем упругости.

В формулы (1 — 7) входят упругие характеристики материала Е, 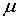, G и К, определяющие его упругие свойства. Однако эти характеристики не являются независимыми. Для изотропного материала независимыми упругими характеристиками являются две, в качестве которых обычно выбираются модуль упругости Е и коэффициент Пуассона 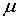. Чтобы выразить модуль сдвига G через Е и 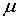, рассмотрим плоскую деформацию сдвига под действием касательных напряжений 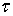(рис. 2). Для упрощения выкладок используем квадратный элемент со стороной а. Вычислим главные напряжения 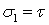, 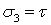. Эти напряжения действуют на площадках, расположенных под углом 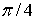к исходным площадкам. Из рис. 2 найдем связь между линейной деформацией 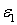в направлении действия напряжения 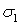и угловой деформацией 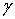. Большая диагональ ромба, характеризующая деформацию 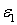, равна

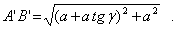
Для малых деформаций

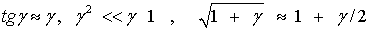
С учетом этих соотношений

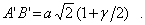
До деформации эта диагональ имела размер 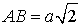. Тогда будем иметь

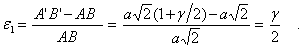
Из обобщенного закона Гука (5) получим

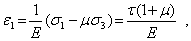
откуда

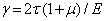
Сравнение полученной формулы с записью закона Гука при сдвиге (6) дает

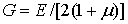(8)

Сложим три соотношения упругости (5)

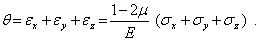(9)

В итоге получим

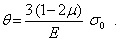
Сравнивая это выражение с объемным законом Гука (7), приходим к результату

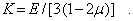
Механические характеристики Е, 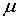, G и К находятся после обработки экспериментальных данных испытаний образцов на различные виды нагрузок. Из физического смысла все эти характеристики не могут быть отрицательными. Кроме того, из последнего выражения следует, что коэффициент Пуассона для изотропного материала не превышает значения 1/2. Таким образом, получаем следующие ограничения для упругих постоянных изотропного материала:

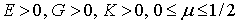
Предельное значение 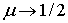приводит к предельному значению 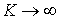, что соответствует несжимаемому материалу ( 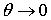при 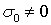). В заключение выразим из соотношений упругости (5) напряжения через деформации. Запишем первое из соотношений (5) в виде

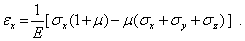
С использованием равенства (9) будем иметь

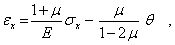
откуда

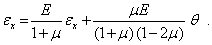
Аналогичные соотношения можно вывести для 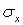и 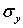. В результате получим

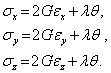(10)

Здесь использовано соотношение (8) для модуля сдвига. Кроме того, введено обозначение

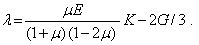
ПОНЯТИЕ О СОСТАВНЫХ БАЛКАХ

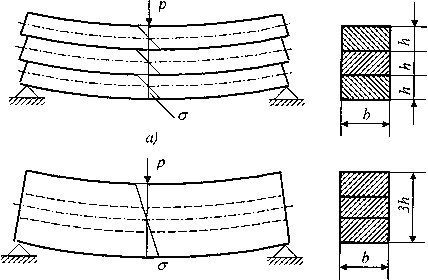
Работу составных балок проиллюстрируем на простом примере трехслойной балки прямоугольного поперечного сечения. Если слои между собой не связаны и силы трения между ними отсутствуют, то каждый из них деформируется как отдельная балка, имеющая свой нейтральный слой (рис. 1, а). Нагрузка между этими балками распределяется пропорционально их жесткостям при изгибе (в данном примере поровну). Это означает, что моменты инерции и моменты сопротивления трех независимо друг от друга деформирующихся балок должны быть просуммированы

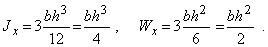
Если скрепить балки сваркой, болтами или другим способом (рис. 1, б), то с точностью до пренебрежения податливостью наложенных связей сечение балки будет работать как монолитное с моментом инерции и моментом сопротивления, равным

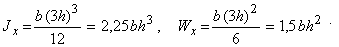
Как видно, при переходе к монолитному сечению жесткость балки возрастает в девять раз, а прочность—в три раза. В инженерной практике наиболее распространены сварные двутавровые балки.

б)

а) несвязанная конструкция, б) связанная сварная конструкция
Рис.1. Расчетные схемы составных балок:

Общие понятия.

К числу статически неопределимых балок может быть отнесена балка на упругом основании. Так называется балка, опирающаяся по всей своей длине (Рис.1) на упругое основание, оказывающее в каждой точке на балку реакцию, пропорциональную у — прогибу балки в этой точке. Коэффициент пропорциональности обозначается буквой k.

Введение предположения о пропорциональности реакций прогибу является приближением, хотя и достаточно близким к действительным условиям.

Рис.1. Расчетная схема балки на упругом основании.

Предложение ввести в расчет коэффициент пропорциональности к, именуемый «коэффициентом постели», было впервые сделано русским академиком Николаем Ивановичем Фуссом в 1801 году. Принимая это предположение, получаем, что интенсивность реакции основания в каждой точке сила равна ky и измеряется в единицах силы и длины; размерность коэффициента k при этом будет сила и квадрат длины. Будем считать, что основание оказывает реакцию при прогибах балки как вниз, так и вверх.

На практике задачи о расчете балки на упругом основании встречаются в железнодорожном деле (рельс, шпала), в строительстве — фундаменты различных сооружений, передающие нагрузку на грунт.

Статически неопределимой такая балка будет потому, что условие статики— сумма нагрузок равна всей реакции основания — не дает возможности установить распределение этой реакции по длине балки, а значит, вычислить изгибающие моменты и поперечные силы.

Интенсивность реакции в каждой точке связана с прогибами балки. Поэтому для решения задачи необходимо найти сначала уравнение изогнутой оси 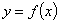, а уже затем формулы для вычисления изгибающего момента и поперечной силы. Ход решения оказывается обратным обычному.

Найдем уравнение изогнутой оси для балки постоянного сечения, лежащей на упругом основании и нагруженной сосредоточенными силами 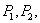... (Рис.1). Начало координат возьмем в любой точке, ось х направим вправо, ось у вертикально вверх. Направление нагрузок вверх будем считать положительным. Напишем обычное дифференциальное уравнение изгиба

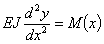
Так как М(х) нам неизвестен, то постараемся связать прогибы непосредственно с нагрузкой, для этого дифференцируем дважды предыдущее уравнение:

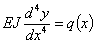(1)

где q(x)—интенсивность сплошной нагрузки, действующей на балку в сечении с абсциссой х.

Сплошной нагрузкой для нашей балки является лишь реакция упругого основания. Интенсивность ей пропорциональна прогибам; эта нагрузка направлена вверх, т. е. положительна, когда прогибы идут вниз, т. е. отрицательны, и наоборот. Таким образом, эта нагрузка имеет знак, обратный знаку прогибов:

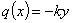
Тогда

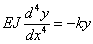	(2)
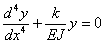	(3)

Если обозначить 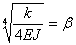, то общий интеграл уравнения (25.3) имеет вид: 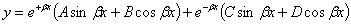(25.4)

Постоянные А, В, С, D должны быть определены в каждом частном случае нагрузки и длины балки. Величина 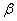имеет измерение обратное длине.

Постановка задачи.

Кроме рассмотренных способов вычисления прогибов и углов поворота сечений балок существует более общий метод, пригодный для определения деформаций любых упругих конструкций. Он основан на применении закона сохранения энергии.

При статическом растяжении или сжатии упругого стержня происходит превращение потенциальной энергии из одного вида в другой; часть потенциальной энергии действующего на стержень груза полностью переходит в потенциальную энергию деформации стержня. Действительно, если мы будем нагружать стержень путем постепенного подвешивания к его нижнему концу очень малых грузов dP, то при добавлении каждого такого груза подвешенная уже часть нагрузки опустится и ее потенциальная энергия уменьшится, а потенциальная энергия деформации стержня соответственно увеличится.

Это явление имеет место при любом виде деформации всякой упругой конструкции при статической нагрузке; такую конструкцию можно рассматривать как своеобразную машину, преобразующую один вид потенциальной энергии в другой.

Мы условились называть «статической» такую нагрузку, которая возрастает постепенно и таким образом, что ускорениями элементов конструкции можно пренебречь; передача давлений (сил) от одной части конструкции на другую не меняет характера движения, этих частей, т. е. их скорость остается постоянной и ускорение отсутствует.

При этих условиях деформация конструкции не будет сопровождаться изменением кинетической энергии системы, и будет иметь место лишь преобразование потенциальной энергии из одного вида в другой. При этом мы пренебрегаем магнитными, электрическими и тепловыми явлениями, сопровождающими упругие статические деформации тела лишь в очень слабой мере.

Так как характер движения всех элементов конструкции с течением времени не меняется, то в каждый момент времени будет иметь место равновесие как для каждой части конструкции в целом под действием внешних сил и реакций, так и для каждого элемента этой части под действием внешних сил и напряжений, приложенных к этому элементу. Деформации конструкции, напряжения в ее частях и реакции, передающиеся от одной части на другую, успевают следовать за ростом нагрузки.

Таким образом, можно сказать, что полное преобразование одного вида потенциальной энергии в другой имеет место, если деформация происходит без нарушения равновесия системы. Мерой энергии, превратившейся в другой вид, является величина работы, произведенной силами, действующими на конструкцию.

Обозначим величину накопленной потенциальной энергии деформации через U, а уменьшение потенциальной энергии внешних нагрузок 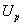. Тогда величина 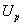измеряется положительной работой этих нагрузок 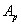, с другой стороны, накоплению потенциальной энергии деформации U соответствует отрицательная работа внутренних, междучастичных сил А, так как перемещения точек тела при деформации происходят в обратном по отношению к внутренним силам направлении.

Закон сохранения энергии при деформациях упругих систем принимает вид:

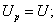
заменяя в этой формуле величины 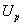и U численно равными им значениями работ 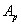и —А, получаем иную формулировку этого закона:

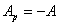или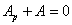

Эта формулировка закона сохранения энергии совпадает с так зазываемым «началом» возможных перемещений в применении к упругим системам. Последнее равенство выражает, что при перемещениях без нарушения равновесия сумма работ всех сил, приложенных к точкам тела, равна нулю.

Таким образом, начало возможных перемещений в применении к упругим системам является следствием закона сохранения энергии.

Таким образом, потенциальная энергия деформации 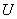численно равна работе внешних сил 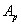, проделанной ими этой деформации:

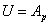
Примеры приложения теоремы Кастильяно.

Определим (Рис.4) прогиб свободного конца В балки, защемленной другим концом А. Балка нагружена сосредоточенной силой, приложенной в точке В. В данном случае возможно непосредственное применение теоремы Кастильяно, так как отыскивается прогиб сечения, где приложена сосредоточенная сила Р

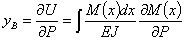
Рис.4. Пример расчетной схемы для расчета перемещений.

Начало отсчета абсциссы х сечения можно выбирать произвольно, лишь бы формула для М (х) была возможно проще. Отсчитывая х от точки В, получаем для момента в любом сечении балк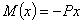и

и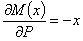

Подставляя эти значения в формулу для 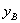и интегрируя, чтобы охватить всю длину балки от 0 до l, получаем:

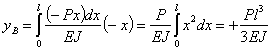
Лекция № 34. Теоремы о взаимности работ и Максвелла — Мора.

Пользуясь понятием о потенциальной энергии, можно установить следующую зависимость между деформациями в различных сечениях балки.

Если к балке, нагруженной силой приложить затем статически силу в сечении 2, то к прогибу точки приложения силы от этой же силы 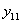прибавится (Рис.1) прогиб от силы , равный 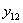; первый значок у буквы у указывает точку, для которой вычисляется прогиб; второй — обозначает силу, вызывающую этот прогиб.

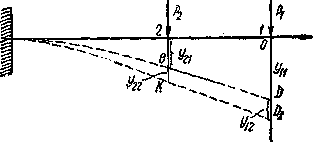
Рис.1. Расчетная схема к теореме о взаимности работ

Полная работа внешних сил составится из трех частей: работы силы на вызванном ею прогибе 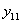, т. е. 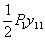, работы силы на вызванном ею прогибе ее точки приложения 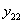, т. е. 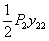, наконец, работы силы на прогибе ее точки приложения от силы , т. е. .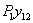

Таким образом, накопленная в стержне при действии обеих сил энергия будет равна:

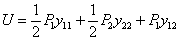
Это количество энергии деформации зависит лишь от конечных значений сил и прогибов и не зависит от порядка нагружения.

Если к балке, загруженной силой , приложить затем силу то, повторив цепь вычислений, получим:

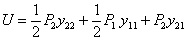
Сравнивая оба значения U, получаем:

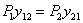
т. е. работа силы (или первой группы сил) на перемещениях, вызванных силой (второй группой сил), равна работе силы на перемещениях, вызванных силой .

Это и есть теорема о взаимности работ. Ее можно сформулировать и иначе: работа первой силы ( ) при действии второй ( ) равна работе второй силы при действии первой.

Теорема Максвелла—Мора.

Прогиб балки в точке приложения сосредоточенной силы Р равен:

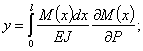
аналогичное выражение мы имеем и для угла поворота с заменой производной 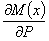на 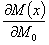. Выясним, что представляют собой эти производные.

Если на балке расположена какая угодно нагрузка из сосредоточенных сил , , ,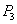..., моментов 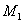, ,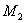..., сплошных нагрузок 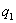, 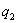..... то момент М(х) в любом сечении такой балки выражается линейной функцией от нагрузок:

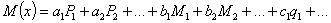
Рис.2. Частная расчетная модель метода Максвелла — Мора.

Коэффициенты 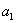, ,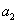..., , 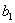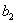…, , 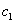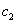... являются функциями пролета балки, расстояний точек приложения сил и моментов от опор и абсциссы х взятого сечения. Пусть мы отыскиваем прогиб точки приложения силы ; тогда

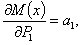
так как , ,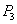..., , 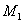,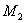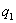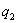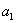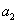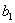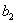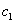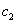..., , ..., , ,..., , …, , ... при этом дифференцировании постоянны. Но 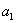можно рассматривать как численную величину момента М в любом сечении балки от действия так называемой единичной нагрузки, т. е. силы 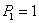; действительно, подставляя в формулу вместо его частное значение, единицу, и приравнивая все остальные нагрузки нулю, получаем .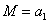

Например, для балки, изображенной на Рис2, а, изгибающий момент равен:

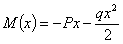
Производная 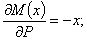; но это как раз и будет выражение изгибающего момента нашей балки, если мы ее нагрузим силой 1, приложенной в той же точке В, где расположена сила Р (Рис.2, б), и направленной в ту же сторону.

Аналогично, производная изгибающего момента М (х) по паре сил 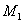численно представляет собой изгибающий момент от пары с моментом, равным единице, приложенной в том же сечении, где имеется пара 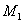, и направленной в ту же сторону. Таким образом, вычисление производных изгибающего момента можно заменить вычислением изгибающих моментов от единичной нагрузки. Эти моменты мы будем обозначать буквой .

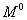Таким образом, для отыскания перемещения 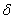(прогиба или угла поворота) любого сечения балки, вне зависимости от того, приложена или не приложена в этом сечении соответствующая сила, необходимо найти выражение для изгибающего момента М от заданной нагрузки и момента 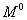от соответствующей единичной нагрузки, приложенной в сечении, где ищем перемещение 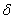; тогда это перемещение выразится формулой

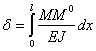
Эта формула была предложена Максвеллом в 1864 г. и введена в практику расчета О. Мором в 1874 г. Если мы в полученном выражении под 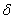подразумеваем прогиб, то момент 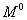надо вычислять от сосредоточенной единичной силы, приложенной в той точке, где мы отыскиваем прогиб; при вычислении же угла поворота в качестве единичной нагрузки прикладывается пара сил с моментом, равным единице.

Для примера рис.2 имеем:

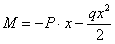	(рис.2,а)
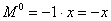	(рис.2, б)

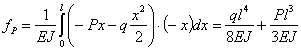
Знак плюс означает, что направление перемещения совпадает с направлением единичной нагрузки, знак минус — наоборот.

Если при определении изгибающих моментов придется делить балку на участки, то соответственно и ин