Момент инерции относительно оси

Моментом инерции тела (системы) относительно данной оси Oz называется величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний h_i до этой оси

Но

Аналогично определяются моменты

инерции системы относительно

осей Ox и Oy

Момент инерции относительно центра

Моментом инерции тела (системы) относительно центра O называется скалярная величина, равная сумме произведений массы каждой точки тела (системы) на квадрат ее расстояния до этого центра

Радиус инерции

Если момент инерции системы относительно оси Ox равен J_x, а ее масса – М, то величина

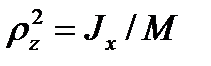
называется радиусом инерции системы относительно оси Oх Радиус инерции определяет расстояние от оси Oх до точки,

в которой нужно сосредоточить всю массу тела (системы),

чтобы момент инерции этой точки был равен моменту

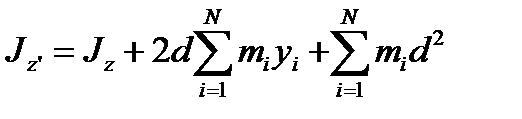инерции всего тела (системы)

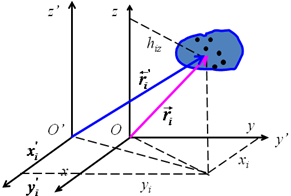Теорема Гюйгенса

Если ось Oz проходит через центр масс системы, то

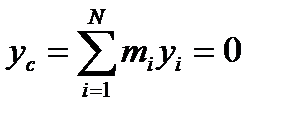
Момент инерции системы относительно данной оси равен моменту инерции относительно оси, ей параллельной и проходящей через центр масс тела, плюс произведение его массы системы на квадрат расстояния между осями

Система уравнений движения

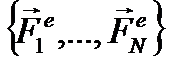Пусть дана механическая система, состоящая из N взаимодействующих точек,на которую действуют внешние силы

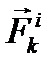Равнодействующую всех внутренних сил, действующих на k-ю точку со стороны других точек, обозначим так:

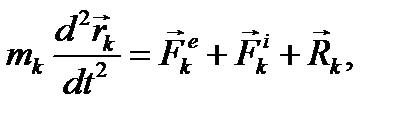Тогда для каждой k-ойточки системы в инерциальной системе координат Oxyz уравнение движение имеет вид

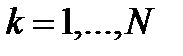
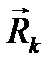
где - силы реакций связей, наложенных на k-ю точку

Число этих уравнений равно N, а общее решение зависит в общем случае от 6N произвольных скалярных постоянных

Теорема о движении ЦМ

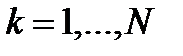
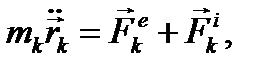Уравнения движения системы имеют вид

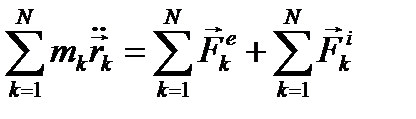Чтобы найти закон движения ЦМ системы, просуммируем эти уравнения

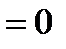
Теорема о движении ЦМ

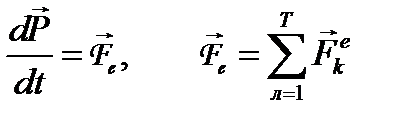
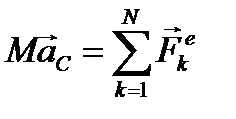
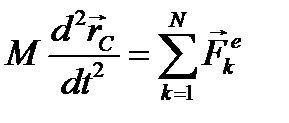Центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему

Теорема о сохранении движения ЦМ

Пусть сумма всех внешних сил, действующих на систему равна нулю

Теорема о движении ЦМС

Если сумма внешних сил действующих на систему равна нулю, то ее ЦМ движется равномерно и прямолинейно.

Если в начальный момент времени ЦМ покоился, то он останется в покое и в дальнейшем. Если сумма проекций внешних сил на какую-нибудь ось (например ось x) равна нулю, то вдоль этой оси ЦМС движется равномерно и прямолинейно или покоится, если он покоился в начальный момент времени

Дифференциальная форма теоремы

Строго говоря, основной закон динамики для точки имеет вид:

Аналогично для системы

Суммируя по всем точкам, имеем