Скорости и ускорения точек ТТ

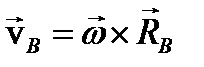
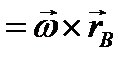
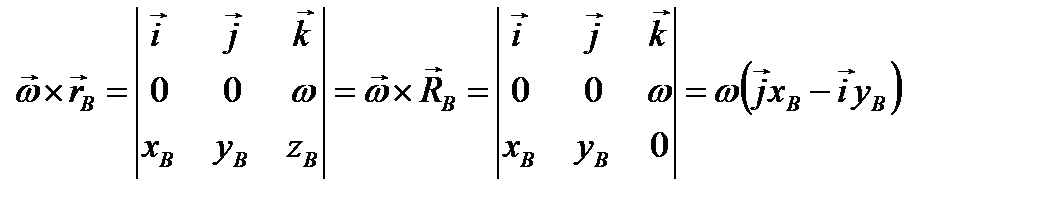
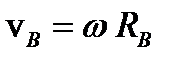Определим теперь ускорение точки В

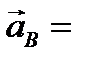
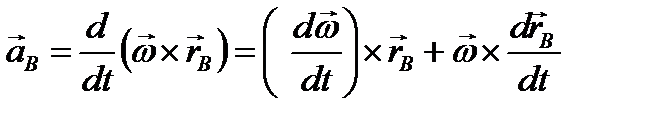
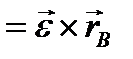
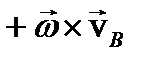
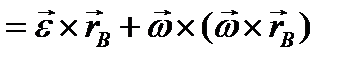
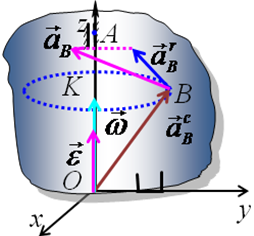
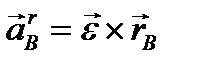
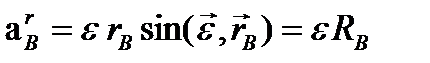
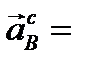
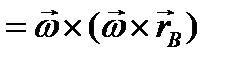
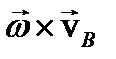-центростремительное ускорение

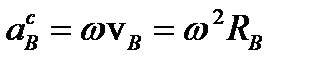
Вращение относительно произвольной оси

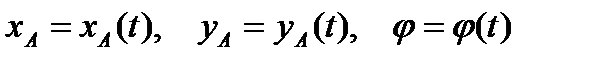
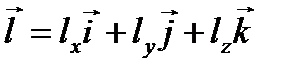В общем случае твердое тело может вращаться относительно оси , не совпадающей по направлению ни с одной из осей данной системы координат. Угловая скорость вращения тела вокруг оси снова можно определить соотношением

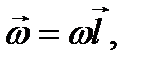
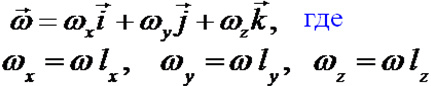
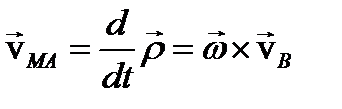
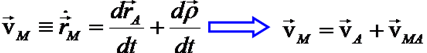
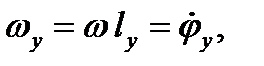
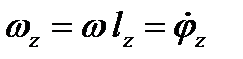
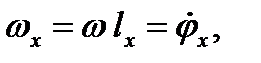
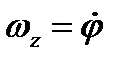Если l_x=l_y=0, то тело вращается вокруг оси Oz и, как мы установили, , где φ – угол поворота тела вокруг этой оси. Аналогично, если ввести углы поворота тела φ_x, φ_y и относительно двух других осей, то

Т.о., вращение тела относительно произвольной оси можно представить как суперпозицию вращений относительно трех осей неподвижной декартовой системы отсчета

Передаточные механизмы

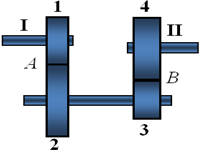Вал I вращается с угловой скоростью ω₁. Определить угловую скорость вращения вала II, если радиусы колес (шестерней) механизма равны r₁, r₂, r₃, r₄. Колесо 1 жестко скреплено с валом I, поэтому

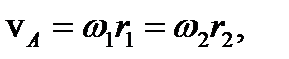
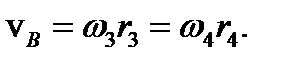w_I = w₁ Аналогично w₄ = w_II Приравнивая скорости в точках A и B контакта колес, получим

Учитывая, что колеса 2 и 3 жестко скреплены, получаем

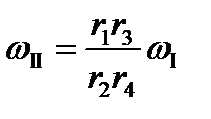
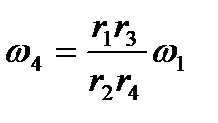
Движение твердого тела называется плоским(плоскопараллельным), если все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости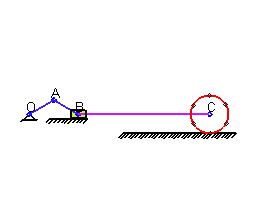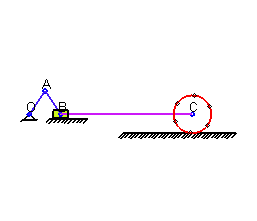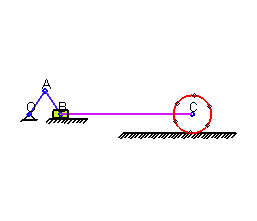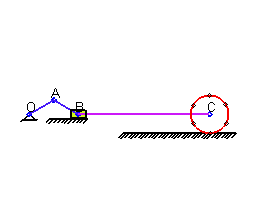

Иллюстрация работы кривошипно-шатунного механизма. Передача движения колесу

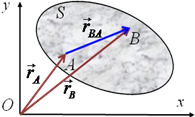Уравнение плоского движения

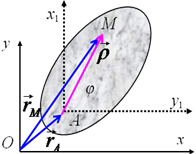
Будем описывать движение сечения S

относительно неподвижной системы координат

Oxy, жестко связанной с плоскостью P

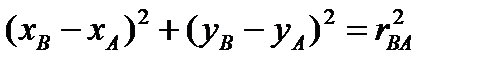Положение сечения относительно этой системы координат определяется положением какого- либо принадлежащего ему отрезка AB

Т.о., плоское движение ТТ слагается из поступательного

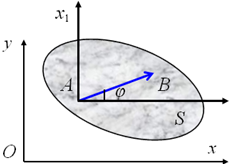движения вместе с полюсом и вращения вокруг полюса

Этим степеням свободы соответствует движение вдоль осей Оу и Ох и вращение относительно

некоторой точки

Введем вспомогательную систему координат с

началом в точке А (полюсе) тела и осями параллельными соответствующим осям неподвижной системы координат

Скорость точек тела при плоском движении

Скорость произвольной точки М находится дифференцированием закона движения

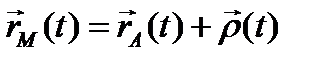
где введена скорость движения точки М относительно полюса А

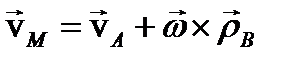
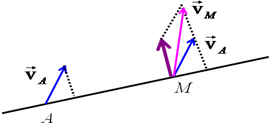
Скорость произвольной точки М ТТ, совершающего плоское движение, геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости этой точки в ее вращении вместе с телом вокруг полюса

Теорема о скоростях двух точек

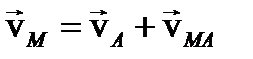следствие 1

Проекции скоростей двух точек сечения S на прямую, их соединяющую, равны

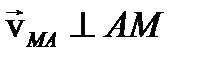Для доказательства достаточно спроецировать уравнение скоростей на прямую АМ и учесть, что

Следствие 2Если точки А, В и С сечения S лежат на одной прямой, то концы векторов скоростей этих точек, тоже лежат на одной прямой, причем

Теорема о МЦС

Мгновенным центром скоростей (МЦС) сечения тела (или плоской фигуры) называется точка, скорость которой в данный момент времени равна нулю

Теорема: Если угловая скорость рассматриваемого сечения S в данный момент времени отлична от нуля, то мгновенный центр скоростей существует и единственен

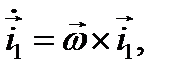
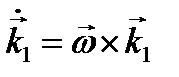
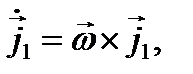Действительно, рассмотрим сечение S

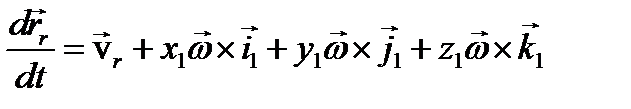
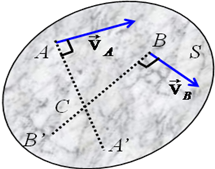Пусть в некоторый момент времени t точки A и B

имеют скорости, не параллельные друг другу

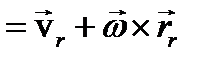
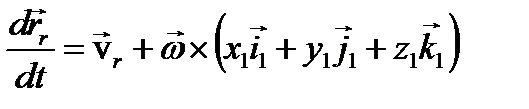Это следует из теоремы о проекциях скоростей, так

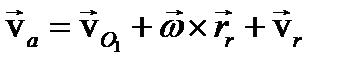как если бы скорость была отлична от нуля, то

она одновременно должна была бы быть перпендикулярна к АА’ и BB’. Последнее, однако,не возможно в силу непараллельности скоростей точек А и В