Дифференциал функции в точке

Опр. Диф-м функции в х₀ наз. линейная относительно приращения аргумента часть приращения функции в этой точке, эквивалентная всему приращению.

d f(х₀)= f ′ (х₀) ∆х; ∆х=dх; df(х₀)= f ′ (х₀) dх

Геометрический смысл. Уравнение касательной в х₀ эквивалентно уравнению

у=f(х₀)+ f ′ (х₀) ∆х (***)

сравнивая (**) и (***) видим, что расстояние от точки Р(х, f(x)) на графике до точки Q (x, f(х₀)+ f ′ (х₀) ∆х) на касательной равно α(∆х)∆х, т.е. является бесконечно малой более высокого порядка, чем ∆х, когда ∆х→0.

Вывод: геометрический смысл дифференцируемости f(x) в точке х₀ состоит в том, что расстояние от точки на ее графике до соответствующей на касательной стремится к нулю "быстрее", чем ∆х.

Производные и дифференциалы высших порядков

Производные и дифференциалы высших порядков

Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции f и обозначается f". Таким образом,

f"(x) = (f'(x))'.

Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f⁽ⁿ⁾. Итак,

f⁽ⁿ⁾(x) = (f^(n-1)(x))', n ϵ N, f⁽⁰⁾(x) = f(x).

Число n называется порядком производной.

Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом,

dⁿf(x) = d(d^n-1f(x)), d⁰f(x) = f(x), n ϵ N.

Если x - независимая переменная, то

dx = const и d²x = d³x = ... = dⁿx = 0.

В этом случае справедлива формула

dⁿf(x) = f⁽ⁿ⁾(x)(dx)ⁿ.

Теоремы Ролля,Лагранжа и Коши.

Теорема Ролля

Пусть функция f: [a, b] → R непрерывна на сегменте [a, b], и имеет конечную или бесконечную производную внутри этого сегмента. Пусть, кроме того, f(a) = f(b). Тогда внутри сегмента [a, b] найдется точка ξ такая, что f'(ξ) = 0.

Теорема Лагранжа

Если функция f: [a, b] → R непрерывна на сегменте [a, b] и имеет конечную или бесконечную производную во внутренних точках этого сегмента, то 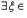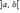такое, что f(b) - f(a) = f'(ξ)(b - a).

Теорема Коши

Если каждая из функций f и g непрерывна на [a, b] и имеет конечную или бесконечную производную на ]a, b[ и если, кроме того, производная g'(x) ≠ 0 на ]a, b[, то 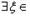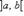такое, что справедлива формула

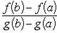
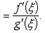
Если дополнительно потребовать, чтобы g(a) ≠ g(b), то условие g'(x) ≠ 0 можно заменить менее жестким:

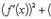
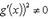
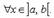
26.Правило Лопиталя
Правило Лопиталя

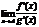Теорема (правило Лопиталя). Пусть А – число, символ одностороннего предела (А=а±0) или символ бесконечности (А=±∞). Пусть функции ƒ(х) и g(х) либо обе бесконечно малые, либо обе бесконечно большие при х→А. Тогда, если существует предел

(конечный или бесконечный),

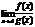
то существует и предел при этом выполняется равенство:

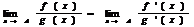
Доказательство:

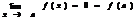Доказательство теоремы дадим в случае, когда ƒ(х) и g(х) – бесконечно малые функции и А=а – число. Изменим, если это необходимо, определение функций ƒ(х) и g(х) в точке а так, чтобы значения этих функций в точке а были бы равны нулю: ƒ(х) = g(х)=0. Так как

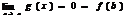и

то ƒ(х) и g(х) непрерывны в точке а,и к этим функциям можно применить теорему Коши. Учитывая, что ƒ(а) = ƒ(b)=0, получим

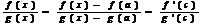
для некоторой точки с, расположенной между точками а и х. При х→а имеем с→а и, следовательно если ƒ(х)→0 и g(х)→0 (соответственно, |ƒ(х)|→+∞, |g(х)|→+∞), когда а→А.Правило Лопиталя позволяет во многих случаях найти предел вида

или, иными словами, раскрыть неопределенность.

В ряде случаев по правилу Лопиталя удается раскрыть неопределенности вида

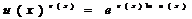Для этого следует воспользоваться тождеством

которое приводит указанные неопределенности к виду 0•х.

Формула Тейлора

Формула Тейлора.

Пусть функция f(x) имеет n производных в точке x₀. Многочлен

T(x) = f(x₀) + ( (f’(x₀))/1! )(x – x₀)¹ + (f ”(x₀))/2!(x – x₀)² +…+ (f ⁽ⁿ⁾(x₀))/n!(x – x₀)ⁿ

Называется n-м многочленом Тейлора функции f(x) в точке x₀.

Пусть функция f(x) имеет в ε – окрестности точки x₀ (n + 1) производных. Тогда для любой точки х из этой окрестности найдется точка с, расположенная между точками х и х₀, для которой выполняется следующая формула

F(x) = T(x) + ( f⁽ⁿ⁺¹⁾(c) / (n + 1)!)(x – x₀)ⁿ⁺¹ – формула Тейлора,

где Т(x) – n-й многочлен Тейлора функции f(x) в точке х₀,

r_n(x) = ( f⁽ⁿ⁺¹⁾(c) / (n + 1)!)(x – x₀)ⁿ⁺¹ – остаточный член в формуле Лагранжа.

Предположим, что (n+1)-я производная функция f(x) ограничена в окрестности точки х₀. Тогда r_n(x) является бесконечно малой более высокого порядка, чем (х-х₀)ⁿ при х ® х₀. (lim (r_n(x)/(х-х₀)ⁿ) = lim [((f⁽ⁿ⁺¹⁾(c))/(n+1)!)(x-x₀)] = 0 – в силу

^{Х®Хо Х®Хо}

Ограниченности f⁽ⁿ⁺¹⁾ (c) в окрестности х₀.) Следовательно ошибка в приближенном равенстве f(x) » T_n(x) (*) также является бесконечно малой более высокого порядка, чем (х – х₀)ⁿ, когда х ® х₀.

Формула (*) применяется для приближенных вычислений.

Используя равенство (*) можно подучить, например следующие формулы (при х®0):

1) (1+x)^a » 1 + (a/1!)x + (a(a-1)/2!)x² +…+ (a(a-1)…(a-n+1)/n!)xⁿ,

2) e^x » 1 + x/1! + x²/2! +…+ xⁿ/n!,

3) ln(1+x) » x – x²/2 + x³/3 – x⁴/4 +…+(-1)ⁿ⁺¹xⁿ/n

4) sin x » x – x³/3! + x⁵/5! – x⁷/7! +…+(-1)^kx^2k+1/(2k+1)!,

5) cos x » 1 – x²/2! + x⁴/4! – x⁶/6! +…+(-1)^kx^2k/(2k)!,

где в каждом случае ошибка является бесконечно малой относительно хⁿ.

28.Монотонность и экстремумы функции

Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум)

Определения

Пусть дана функция 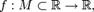и 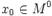— внутренняя точка области определения f. Тогда

§ x₀ называется точкой локального максимума функции f, если существует проколотая окрестность 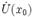такая, что

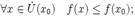
§ x₀ называется точкой локального минимума функции f, если существует проколотая окрестность 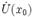такая, что

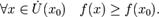
Если неравенства выше строгие, то x₀ называется точкой строгого локального максимума или минимума соответственно.

§ x₀ называется точкой абсолютного (глобального) максимума, если

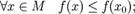
§ x₀ называется точкой абсолютного минимума, если

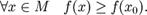
Значение функции f(x₀) называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

• Функция возрастает, если большему значению аргумента соответствует большее значение функции. • Функция убывает если большему значению аргумента соответствует меньшее значение функции.

ОПРЕДЕЛЕНИЯ

Пусть дана функция 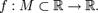Тогда

§ функция f называется возраста́ющей на M, если

.

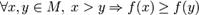§ функция f называется стро́го возраста́ющей на M, если

.

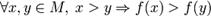§ функция f называется убыва́ющей на M, если

.

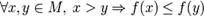§ функция f называется стро́го убыва́ющей на M, если

.

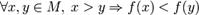(Строго) возрастающая или убывающая функция называется (строго) монотонной.