Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.

Ориентация эллипса и размеры его осей зависят от амплитуд складываемых колебаний и разности фаз a. Рассмотрим некоторые частные случаи, представляющие физический интерес:

1) a = mp(m=0, ±1, ±2, ...). В данном случае эллипс вырождается в отрезок прямой

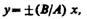(145.3)

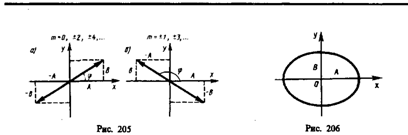
где знак плюс соответствует нулю и четным значениям т (рис. 205, а), а знак минус — нечетным значениям т (рис. 205, б). Результирующее колебание является гармоническим колебанием с частотой w и амплитудой 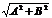, совершающимся вдоль прямой (145.3), составляющей с осью х угол j=arctg 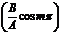. В данном случае имеем дело с линейно поляризованными колебаниями;

2) a = (2m+1) 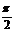(m=0, ± 1, ±2,...). В данном случае уравнение примет вид 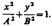(145.4) Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 206). Кроме того, если А=В, то эллипс (145.4) вырождается в окружность. Такие колебания называются циркулярно поляризо­ванными колебаниями или колебаниями, поляризованными по кругу.

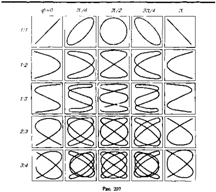
Если частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые тра­ектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу.* Вид этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. На рис. 207 представлены фигуры Лиссажу для различных соотношений частот (указаны слева) и разностей фаз (указаны вверху; разность фаз принимается равной j).

Вопрос 7 Дифференциальное уравнение свободных затухающих колебаний (механических и электромагнитных) и его решение.
Рассмотрим свободные затухающие колебания – колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах, а также омичес­ких потерь и излучения электромагнитной энергии в электрических колебательных системах.
Закон затухания колебаний определяется свойствами колебательных систем. Обыч­но рассматривают линейные системы — идеализированные реальные системы, в кото­рых параметры, определяющие физические свойства системы, в ходе процесса не изменяются. Линейными системами являются, например, пружинный маятник при малых растяжениях пружины (когда справедлив закон Гука), колебательный контур, индуктивность, емкость и сопротивление которого не зависят ни от тока в контуре, ни от напряжения. Различные по своей природе линейные системы описываются идентич­ными линейными дифференциальными уравнениями, что позволяет подходить к изуче­нию колебаний различной физической природы с единой точки зрения, а также проводить их моделирование, в том числе и на ЭВМ.

Дифференциальное уравнение свободных затухающих колебаний линейной системы задается в виде 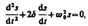(146.1)

где s – колеблющаяся величина, описывающая тот или иной физический процесс, d=const — коэффициент затухания, w₀ — циклическая частота свободных незатуха­ющих колебаний той же колебательной системы, т. е. при d=0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.