Теорема об изменении количества движения механической системы при ударе.

Изменение количества движения механической системы за время удара равно сумме внешних ударных импульсов, действующих на точки системы.

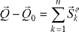
Доказательство. Разделим ударные силы, действующие на каждую точку механической системы, на внешние и внутренние. Запишем основное уравнение удара для каждой точки системы

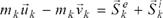
где , 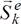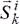- равнодействующие внешних и внутренних ударных импульсов. Суммируя полученные равенства, с учетом свойства внутренних сил находим:

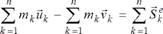
Следствие. При действии на механическую систему лишь внутренних ударных импульсов количество движения системы не изменяется.

39)ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ

ТОЧКИ

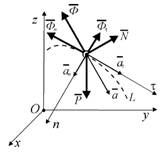
Рассмотрим движение материальной точки массой m в пространствеинерциальной системы отсчета Oxyz(рис. 1.1). Пусть точка движется под дей-

ствием активных сил, равнодействующая которых F . На точку наложены связи,N – равнодействующая сил реакций этих связей. Дифференциальное уравнениедвижения точки может быть записано в виде

ma = F+N .

Это уравнение можно записать такF + N + (−ma) = 0Обозначим Ф = −ma, назовем эту силу – силой инерцииточки.ПолучимF+ N+Ф= 0. В таком случае можносформулировать принцип Даламбера для материальной точки:

В каждый момент времени активные силы, действующие на материальную точку силы реакции связей вместе с силой инерции точки, образуютуравновешенную систему сил

.

ПРИНЦИП ДАЛАМБЕРА ДЛЯ МЕХАНИЧЕСКОЙ

СИСТЕМЫ

Рассмотрим движение механической системы { k }n M материальных точекв пространстве инерциальной системы отсчета xOy.

Пусть { e}k n

F – внешние силы, действующие на точки системы, а{ i}k n

F внутренние силы системы. ak– ускорение некоторой точки Mk, массакоторой mk. Φk = −mkak– сила инерции этой точки.

Рис. 1

Принцип Даламбера для отдельной точки записывается в виде:( e i ) 0Φk ,Fk ,Fk∼.

Для всей механической системы его можнопредставить так:({ e} ;{ i} ;{ } )k kkn n nF FΦ ∾0. (2.1)

Силы внешние и внутренние, действующие на М.С. вместе с силами инерции частиц системы образуют уравновешенную систему сил

.

Главный вектор и главный момент сил инерции твёрдого тела.

Система сил инерции твёрдого тела можно заменить одной силой, равной 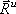и приложенной в центре О, и парой с моментом, равным 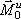. Главный вектор системы сил, как известно, не зависит от центра приведения и может быть вычислен заранее. Т.к. 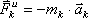, то

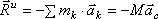
Следовательно, главный вектор сил инерции тела, совершающего любое движение, равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.

Прикладывается главный вектор к точке приведения, которую можно назначить в любом месте, т.е. он не зависит от выбора этой точки.

Если ускорение 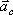разложить на касательное и нормальное, то вектор 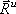разложиться на составляющие

, .
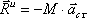
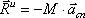