Кратные, криволинейные и поверхностные интегралы.
Векторный анализ.
371-380.Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах 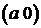 .
.
371. 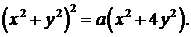
372. 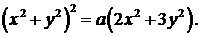
373. 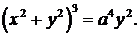
374. 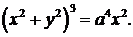
375. 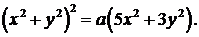
376. 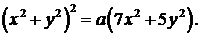
377. 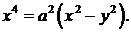
378. 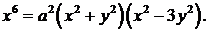
379. 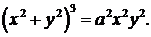
380. 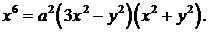
381-390.Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость 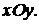
381. 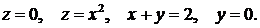
382. 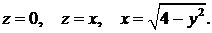
383. 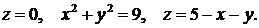
384. 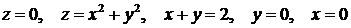
385. 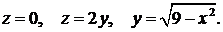
386. 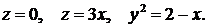
387. 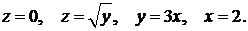
388. 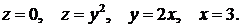
389. 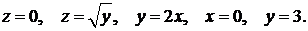
390. 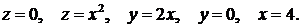
391.Вычислить криволинейный интеграл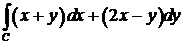 вдоль окружности
вдоль окружности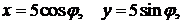 обходя ее против хода часовой стрелки. Сделать чертеж.
обходя ее против хода часовой стрелки. Сделать чертеж.
392.Вычислить криволинейный интеграл 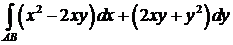 вдоль параболы
вдоль параболы 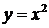 от точки А(1;1) до точки В(2;4). Сделать чертеж.
от точки А(1;1) до точки В(2;4). Сделать чертеж.
393. Вычислить криволинейный интеграл 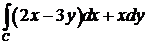 вдоль эллипса
вдоль эллипса 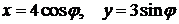 , обходя его против хода часовой стрелки. Сделать чертеж.
, обходя его против хода часовой стрелки. Сделать чертеж.
394. Вычислить криволинейный интеграл 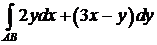 вдоль параболы
вдоль параболы 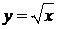 от точки А(1;1) до точки В(4;2). Сделать чертеж.
от точки А(1;1) до точки В(4;2). Сделать чертеж.
395.Вычислить криволинейный интеграл 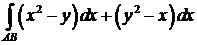 от точки
от точки 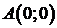 до точки
до точки 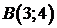 вдоль прямой, проходящей через эти точки. Сделать чертеж.
вдоль прямой, проходящей через эти точки. Сделать чертеж.
396. Вычислить криволинейный интеграл 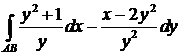 от точки
от точки 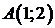 до точки
до точки 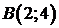 вдоль прямой проходящей через эти точки. Сделать чертеж.
вдоль прямой проходящей через эти точки. Сделать чертеж.
397.Вычислить криволинейный интеграл 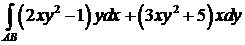 от точки
от точки 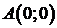 до точки
до точки 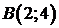 вдоль прямой, проходящей через эти точки. Сделать чертеж.
вдоль прямой, проходящей через эти точки. Сделать чертеж.
398.Вычислить криволинейный интеграл 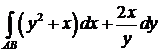 вдоль кривой
вдоль кривой 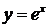 от точки
от точки 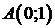 до точки
до точки 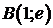 . Сделать чертеж.
. Сделать чертеж.
399.Вычислить криволинейный интеграл 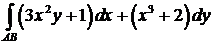 вдоль параболы
вдоль параболы 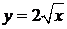 от точки
от точки 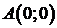 до точки
до точки 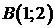 . Сделать чертеж.
. Сделать чертеж.
400.Вычислить криволинейный интеграл 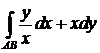 вдоль кривой
вдоль кривой 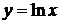 от точки
от точки 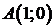 до точки
до точки 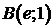 . Сделать чертеж.
. Сделать чертеж.
401-410. Даны векторное поле 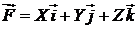 и поверхность
и поверхность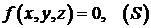 ,которая совместно с координатными плоскостями образует замкнутое тело
,которая совместно с координатными плоскостями образует замкнутое тело 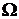 , лежащее в первом октанте. Требуется вычислить: 1) поток векторного поля
, лежащее в первом октанте. Требуется вычислить: 1) поток векторного поля 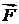 через поверхность
через поверхность 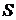 в направлении нормали
в направлении нормали 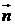 (
( 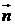 внешняя нормаль к
внешняя нормаль к 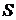 ); 2) двумя способами (непосредственно и по теореме Стокса) найти циркуляцию векторного поля
); 2) двумя способами (непосредственно и по теореме Стокса) найти циркуляцию векторного поля 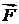 вдоль линии пересечения поверхности
вдоль линии пересечения поверхности 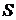 с плоскостями координат и лежащей в первом октанте; 3) двумя способами (непосредственно и по теореме Остроградского-Гаусса) найти поток векторного поля
с плоскостями координат и лежащей в первом октанте; 3) двумя способами (непосредственно и по теореме Остроградского-Гаусса) найти поток векторного поля 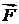 через полную поверхность
через полную поверхность 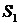 замкнутого тела
замкнутого тела 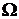 , лежащего в первом октанте, ограниченного поверхность
, лежащего в первом октанте, ограниченного поверхность 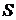 и плоскостями координат. Сделать чертеж.
и плоскостями координат. Сделать чертеж.
401. 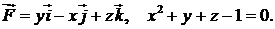
402. 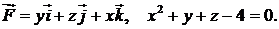
403. 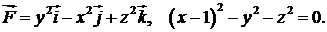
404. 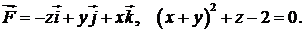
405. 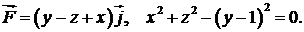
406. 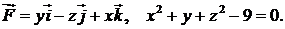
407. 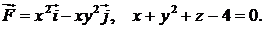
408. 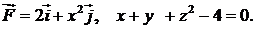
409. 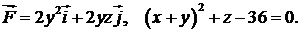
410. 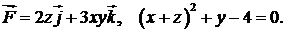
411-420. Проверить, является ли векторное поле 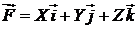 потенциальным и соленоидальным. В случае потенциальности поля
потенциальным и соленоидальным. В случае потенциальности поля 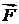 найти его потенциал.
найти его потенциал.
411. 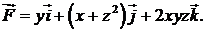
412. 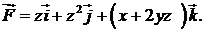
413. 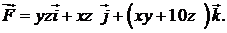
414. 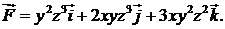
415. 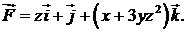
416. 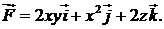
417. 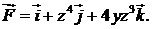
418. 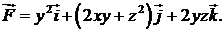
419. 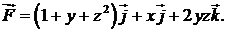
420. 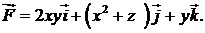
Ряды
421-430.Исследовать сходимость числового ряда 
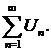
421. 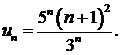 422.
422. 
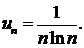
423. 
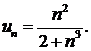 424.
424. 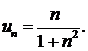
425. 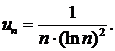 426.
426. 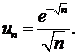
427. 
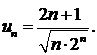 428.
428. 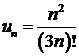 .
.
429. 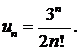 430.
430. 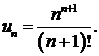
431-440.Найти интервал сходимости степенного ряда 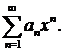
431. 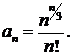 432.
432. 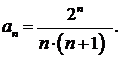
433 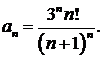 434.
434. 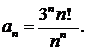
435. 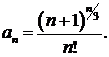 436.
436. 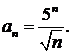
437. 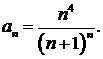 438.
438. 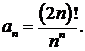
439. 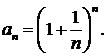 440.
440. 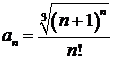
441-450. Вычислить определенный интеграл 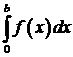 с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем почленно его проинтегрировав.
с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем почленно его проинтегрировав.
441. 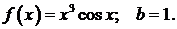 442.
442. 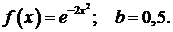
443. 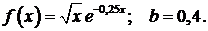 444.
444. 
445. 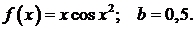 446.
446. 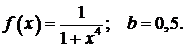
447. 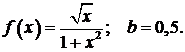 448.
448. 
449. 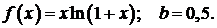 450.
450. 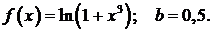
451-460.Найти три первых, отличных от нуля члена разложения в степенной ряд решения 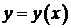 дифференциального уравнения
дифференциального уравнения 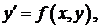 удовлетворяющего начальному условию
удовлетворяющего начальному условию 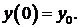
451. 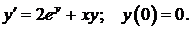 452.
452. 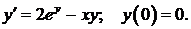
453. 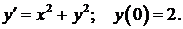 454.
454. 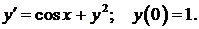
455. 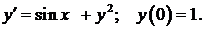 456.
456. 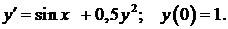
457. 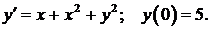 458.
458. 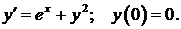
459. 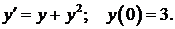 460.
460. 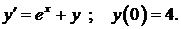
461-470. Разложить данную функцию 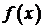 в ряд Фурье в интервале
в ряд Фурье в интервале 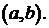
461. 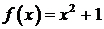 в интервале
в интервале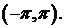
462. 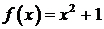 в интервале
в интервале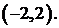
463. 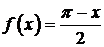 в интервале
в интервале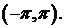
464. 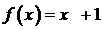 в интервале
в интервале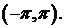
465. 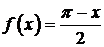 в интервале
в интервале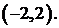
466. 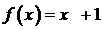 в интервале
в интервале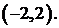
467. 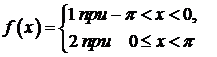 в интервале
в интервале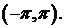
468. 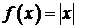 в интервале
в интервале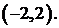
469.Функция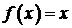 задана в интервале
задана в интервале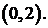 Разложить данную функцию в ряд Фурье в интервале
Разложить данную функцию в ряд Фурье в интервале 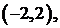 продолжив ее в интервал
продолжив ее в интервал 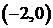 четно.
четно.
470. Функция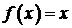 задана в интервале
задана в интервале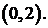 Разложить данную функцию в ряд Фурье в интервале
Разложить данную функцию в ряд Фурье в интервале 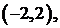 продолжив ее в интервал
продолжив ее в интервал 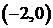 нечетно.
нечетно.
