Дан закон распределения дискретной случайной величины

X
p	0,2	0,4	0,1	0,3

P(X<3) = …

33.Дан закон распределения дискретной случайной величины X:

X
p	0,3	0,1	0,2	p4

Значения p₄ и P(X<7):

1. p4=0,5; P(X<7)=0,4
2. p4=0,4; P(X<7)=0,3
3. p4=0,3; P(X<7)=0,6
4. p4=0,4; P(X<7)=0,5

34.Закон распределения вероятностей дискретной случайной величины

1. 
2. 
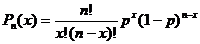
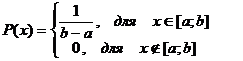
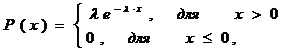3. l>0
4. 
5. 

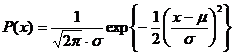
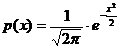
35.Пропущенное значение вероятности в законе распределения дискретной случайной величины c математическим ожиданием M(X)=3 равно …

xi
pi	0,5	0,1	0,2

36.Пропущенное значение x₄ в законе распределения дискретной случайной величины c математическим ожиданием M(X)=3 равно …

xi
pi	0,5	0,1	0,2

37. Даны числовые характеристики двух случайных величин X и Y: MX=3, MY=7, DX=1, DY=2. Значение M(3X+2Y):

A.23;

B.21

C.25

D.28

38. Даны числовые характеристики двух случайных величин X и Y: MX=3, MY=7, DX=1, DY=2. Значение D(4X-Y).

A.2

B.14

C.15

D.18

39. Два стрелка независимо друг от друга стреляют по одной цели. Вероятность попадания в цель первого стрелка равна 0,7; второго – 0,8. Математическое ожидание числа попаданий в цель:

A.1,5

B.0,7

C.0,8

D.1,4

Дана функция распределения случайной величины

F(x)= .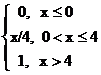

Математическое ожидание X равно:

A.1;

B.3;

C.2;

D.2,5.

Соответствие между формулой и определением

A.Математическое ожидание дискретной случайной величины	A.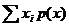
B.Математическое ожидание константы	B. с
C.Математическое ожидание суммы случайных величин	C.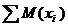

Соответствие между формулой и определением

A.Дисперсия дискретной случайной величины х	A.M(x-Mx)2
B.Дисперсия константы	B.0
C.Дисперсия произведения константы и случайной величины	C.С2Dх

43. Математическое ожидание квадрата отклонения случайной величины от ее математического ожидания называется … случайной величины

Непрерывные случайные величины

Плотность вероятности и интегральная функция распределения

С помощью плотности распределения вероятности можно задать

1. дискретную случайную величину
2. непрерывную случайную величину
3. случайное событие
4. интервальную величину

С помощью дифференциальной функции распределения можно задать

1. дискретную случайную величину
2. непрерывную случайную величину
3. случайное событие
4. интервальную величину

Вероятность каждого конкретного значения непрерывной случайной величины равна

1. 0
2. 0,1
3. 0,5
4. 1

4. Возможное событие …….иметь нулевую вероятность

1. Может
2. Не может
3. Может для непрерывной случайной величины
4. Может для дискретной случайной величины

Непрерывную случайную величину можно задать с помощью

1. таблицы распределения
2. многоугольника распределения
3. функции распределения вероятности
4. плотности распределения вероятности

Свойства плотности вероятности

1. 
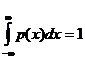
2. p (x) ³ 0
3. 
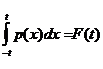
4. p (x) £ 1)
5. (*)

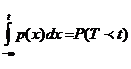Плотность вероятности любой случайной величины находится в пределах

1. от –1 до 1
2. от 0 до 1
3. от 0,5 до 1
4. от 0 до ¥
5. от -¥ до ¥

Кривая, изображающая дифференциальную функцию распределения f(x) случайной величины, называется

1. полигоном распределения
2. многоугольником распределения
3. * кривой распределения
4. гистограммой

Случайная величина задана дифференциальной функцией распределения.

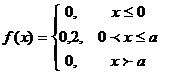
Недостающее значение a=….