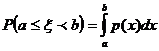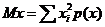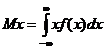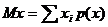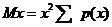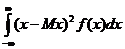Закон распределения случайной величины представлен в таблице

xi
pi	0,008	0,96	0,384	?

Недостающее значение

1. 0,05
2. 0,35
3. 0,512
4. 0,714
5. 1,0

22. Дан закон распределения дискретной случайной величины:

X
P	P1	0,28	0,22	0,14	0,01

P₁=…

23. Дан закон распределения дискретной случайной величины:

X
P	0,35	P2	0,22	0,14	0,01

P₂=…

24. Дан закон распределения дискретной случайной величины:

X
P	0,35	0,28	P3	0,14	0,01

P₃=…

25. Дан закон распределения дискретной случайной величины:

X
P	0,35	0,28	0,22	P4	0,01

P₄=…

26. Дан закон распределения дискретной случайной величины:

X
P	0,35	0,28	0,22	0,14	P5

P₅=…

Закон распределения случайной величины представлен в таблице

xi
pi	0,1	0,2	0,5

Недостающее значение равно …

Закон распределения случайной величины представлен в таблице

xi
pi	0,1	0,2		0,2

Недостающее значение равно …

…

Закон распределения случайной величины представлен в таблице

xi
pi		0,2	0,5	0,2

Недостающее значение равно …

	F(-∞) = 0
30. Основные свойства функции распределения	F(+∞) = 1
	F(x) - не убывающая функция х
	P{ a≤ ξ <b } = F(b) - F(a).
	F(x)=
31. Вероятность того, что дискретная случайная величина ξ примет значение, лежащее в интервале (а,b) равна	P{ a≤ ξ <b } = F(b) - F(a).
	P{ a≤ ξ <b } = F(a) - F(b)
	P{ a≤ ξ <b } = F(a) + F(b)

32. Случайная величина X задана интегральной функцией распределения:

F(x)= ;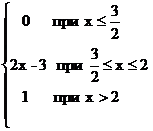

P(1<X<3) равно:

1. 1
2. 0,5
3. 2
4. 0,7

33. Дана интегральная функция распределения случайной величины X:

F(x)= .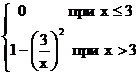

Вероятность попадания в интервал (5;10) равна:

A. * MX=7; P(5<X<10)=0,7;

B. MX=5; P(5<X<10)=0,6;

C. MX=6; P(5<X<10)=0,27;

D. MX=5,5; P(5<X<10)=0,3.

AB	BC	A	D	D	C	D	C	0.6	ABC

A	AB	A	B	D	E	0.4	0.35	0.1	0.2

0.28	0.22	0.14	0.1	0.01	C	C	B	B	A

0.35	0.28	0.22	0.14	0.01	0.2	0.5	0.2	0.1	0.2

0.5	0.2	0.1	ABCD	B	A	D	A

Числовые характеристики дискретной случайной величины

1. Для дискретной случайной величины математическое ожидание определяется по формуле

	0
2. Математическое ожидание константы c равно	с
	1
	2c

	М(х+y) = Мх - Мy
3. Математическое ожидание суммы дискретных случайных величин x и y	М(х+y) = Мх + Мy
	М(х+y) = Мх * Мy
	М(х+y) = Мх + Мy-М(XY)

	Dx = M(x2-Mx)
4. Дисперсия дискретной случайной величины х	Dx = M(x-Mx)2
	Dx = M(x+Mx)2
	Dx = M(x*Mx)2

	DС = С
5. Дисперсия константы c	DС = 0
	DС = МС
	DС = 1
	DС = С2

	D(Сх) = СDх
6. Постоянная величина (С) может быть вынесена за знак дисперсии следующим образом	D(Сх) = С2Dх
	D(Сх) = С3Dх
	D(Сх) = С2

	произведению их дисперсий
7. Дисперсия суммы случайных величин всегда равна	сумме их дисперсий, если эти величины независимы
	сумме их дисперсий
	разности их дисперсий, если эти величины независимы

Закон распределения случайной величины представлен в таблице

xi
pi	0,1	0,2	0,5	0,2

Математическое ожидание данной случайной величины:

1. 2,4
2. 3,84
3. 5,6
4. 7,14
5. 9,0

Закон распределения случайной величины представлен в таблице

xi
pi	0,1	0,2	0,5	0,2

Дисперсия данной случайной величины

1. 2,48
2. 3,04
3. 5,52
4. 7,14

10.Закон распределения случайной величины представлен в таблице

xi
pi	0,1	0,2	0,5	0,2

M(X²) случайной величины X

1. 2,4
2. 3,84
3. 5,6
4. 17,14
5. 29,6
6. 34,4

11.Закон распределения случайной величины представлен в таблице

xi
pi	0,1	0,2	0,5	0,2

Математическое ожидание данной случайной величины:

1. 2,4
2. 3,84
3. 15,6
4. 18,8
5. 19,20

Закон распределения случайной величины представлен в таблице

xi
pi	0,1	0,2	0,5	0,2

Дисперсия данной случайной величины:

1. 12,48
2. 23,04
3. 27,36
4. 31,14
5. 38,16

Закон распределения случайной величины X задан рядом распределения

Xi
Pi	0,3	0,1	0,6

Математическое ожидание:

1. 1,5
2. 2,3
3. 3,9
4. 4,2
5. 5,8