Дифференциал функции, его алгебраический и геометрический смысл.
Свойства дифференциала.
Дифференциал функции равен произведению производной функции на приращение ее аргумента.
Дифференциал функции есть главная часть приращения функции. В этом состоит аналитический смысл дифференциала
Геометрический смысл: дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.
Свойства дифференциала:аналогичны свойствам производной.
Производные и дифференциалы второго и высшего порядков.
Дифференциалом второго порядка (или вторым дифференциалом) от функции y=f(x) в точке х 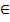 (a; b) называется дифференциал от дифференциала первого порядка функции f(x) в этой точке.
(a; b) называется дифференциал от дифференциала первого порядка функции f(x) в этой точке.
Дифференциалом п-ного порядка от функции f(x) в точке x называется дифференциал от дифференциала (п–1)-го порядка функции f(x) в этой точке:
d 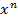 y=d(d
y=d(d 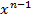 y), где d
y), где d 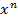 y=f
y=f 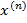 d
d 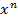 .
.
Производная второго порядка-производная от производной этой функции
Производной n-го порядка функции f(x) наз. производная от производной функции f(x) (n-1)-го порядка 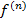 (x)
(x)
Асимптоты функции, их виды, правила нахождения
Асимптоты-линии, к которым график функции неограниченно приближается при стремлении х к бесконечности
1) Вертикальные асимптоты бывают только в точках разрыва функции и на границе области определения
2) Наклонные асимптоты имеют вид y=kx+b
3) Горизонтальные асимптоты
Вертикальная асимптота существует в точках разрыва функции, т. е. в точках, в которых знаменатель дроби равен нулю
Чтобы найти горизонтальную или наклонную асимптоты нужно числитель дроби разделить на знаменатель, т.е. выделить целую часть.
В результате получается:
-если степень числителя меньше степени знаменателя, то y=0 – горизонтальная асимптота;
-если степень числителя равна степени знаменателя, то y=b – горизонтальная асимптота (b = отношению коэффициентов при высших степенях);
Е-сли степень числителя на 1 больше степени знаменателя, то y=kx+b – наклонная асимптота (kx+b – целая часть дробно-рациональной функции).
Критические точки, экстремум функции, промежутки возрастания, убывания.
Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.
Если при переходе через точку х0 производная дифференцируемой функции у=f(x) меняет свой знак с плюса на минус, то точка х0 есть точка минимума функции, а если с минуса на плюс,-то точка минимума
Если функция возрастает на некотором промежутке Х, то производная неотрицательна на этом промежутке: f′(x) 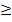 0
0
Если функция убывает на некотором промежутке Х, то производная отрицательна на этом промежутке:f′(x) 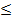 0
0
Промежутки выпуклости, вогнутости, точки перегиба. Схема исследования
Функции
Кривая называется выпуклой на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая называется вогнутой на интервале (а, b), если все ее точки лежат выше любой ее касательной на этом интервале
Точка, отделяющая выпуклую часть кривой отвогнутой, называется точкой перегиба.
Схема исследования функции
1) Область определения функции.
2) Координаты точек пересечения с осями координат.
3) Четность, нечетность функции.
4) Асимптоты графика и пределы на ±∞. (Если они имеются).
5) Критические точки.
6) Интервалы монотонности и точки экстремума.
7) Промежутки выпуклости и вогнутости, точки перегиба. (Если они имеются).
8) Дополнительные точки, если нет асимптот.
9) Построение графика.
10) Область значения функции.
Неопределенный интеграл, его свойства. Методы вычисления неопределенного интеграла: непосредственное интегрирование. Примеры.
Множество всех первообразных для функции f(x) на промежутке Х называется неопределенным интегралом от функции f(x)
Свойства:
1) Производная от неопределенного интеграла равна подынтегральной функции:

2) Дифференциал неопределенного интеграла равен подынтегральному выражению:
D ( ∫ f(x)dx)=f(x)dx
3) Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого С:
∫ df(x)=f(x)+C
4) Постоянный множитель можно выносить за знак интеграла
∫ kf(x)dx=k∫f(x)dx
5) Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций:
∫(f(x)+g(x))dx=∫f(x)dx+∫g(x)dx
6) Пусть функция f(x) имеет первообразнуюF(x), тогда
∫f(kx+b)dx= 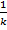 F(kx+b)+C
F(kx+b)+C
Методы вычисления неопределенного интеграла:
1) Метод непосредственного интегрирования ( основан на применении свойств интеграла)
∫(1-sinx)dx=∫dx -∫sinxdx=x+cos+C
2) Метод замены переменной( основан на понятии производной сложной функции)

3) Метод интегрирования по частям (по формуле ∫udv=uv-∫udu)
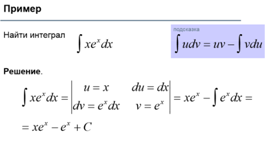
Методы вычисления неопределенного интеграла: интегрирование методом подстановки. Примеры.
Основан на применении свойств интеграла F( 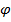 (x))
(x))
Если функция f(t) имеет первооборазнуюF(t), а функция t= 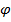 (x) дифференцируема, то функция f(φ(x)) также имеет первообразную:
(x) дифференцируема, то функция f(φ(x)) также имеет первообразную:
∫ f(φ(x))d(φ(x))-F(φ(x)+C

