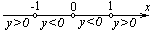Краснодарского края«апшеронский лесхоз-техникум»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ, НАУКИ И МОЛОДЕЖНОЙ ПОЛИТИКИ КРАСНОДАРСКОГО КРАЯГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ПРОФЕССИОНАЛЬНОЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
КРАСНОДАРСКОГО КРАЯ«АПШЕРОНСКИЙ ЛЕСХОЗ-ТЕХНИКУМ»
В помощь студенту 1 курса
Методические указания к самостоятельной работе для студентов 1 курса по математике
(в форме практических работ поалгебре и началам анализа)
2017г.
В данном сборнике собраны задания по основным темам алгебры и начал анализа X-XI класса. Многовариантные проверочные, обучающие и тестовые работы сопровождаются кратким теоретическим напоминанием, таблицами, примерами оформления решений и ответами.
Преподавателю этот сборник заменит дидактические и раздаточные материалы. Учащиеся могут использовать его для самостоятельного изучения пропущенных тем и самоконтроля, а родители - для контроля знаний своих взрослых детей.
Успехов Вам всем!
Разработчик:
Яценко М.М., преподаватель математики
ГБПОУ КК «Апшеронский лесхоз-техникум»
С о д е р ж а н и е
I. Алгебра и начала анализа.
Тема стр.
1. Вычисление производной с помощью определения 4
2. Вычисление производных алгебраических функций 7
3. Вычисление производных сложных функций 10
4. Нахождение наибольшего и наименьшего значений функции 12
5. Свойства функций 15
6. Исследование функции и построение ее графика 17
7. Производная (обобщение, тесты) 20
8. Вычисление первообразных функций 29
9. Вычисление определенного интеграла 32
10. Применение интеграла для вычисления площадей и объемов 35
11. Тригонометрические функции углов поворота 38
12. Преобразование тригонометрических выражений 42
13. Решение тригонометрических уравнений 46
14. Преобразование числовых и буквенных выражений 52
15. Преобразование выражений, содержащих радикалы 53
16. Решение иррациональных уравнений 55
17. Преобразование выражений, содержащих степени с
дробными (рациональными) показателям 56
18. Преобразование выражений, содержащих степени и логарифмы 58
19. Решение рациональных уравнений и неравенств 60
20. Решение показательных уравнений и неравенств 65
21. Решение логарифмических уравнений и неравенств 66
II. Ответы 69
ПРАКТИЧЕСКАЯ РАБОТА №1
«Вычисление производной с помощью определения»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки в теме: «Вычисление производной функции по определению».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности учащихся.
ОБОРУДОВАНИЕ: микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Ответить на контрольные вопросы:
а) Что такое приращение аргумента и приращение функции?
б) В чем состоит геометрический смысл приращений  и
и  ?
?
в) В чем состоит геометрический смысл отношения  ?
?
г) Сформулируйте определение производной функции в точке.
2. С помощью обучающих таблиц повторить планы вычисления приращения функции, производной функции в точке по определению и изучить образцы решенных примеров.
3. Выполнить задания для самоконтроля (в таблице).
ОБУЧАЮЩИЕ ТАБЛИЦЫ
 |
Производная функции.
Определение. Производной функции  в заданной точке xназывается предел отношения приращения функции
в заданной точке xназывается предел отношения приращения функции  в этой точке к приращению аргумента
в этой точке к приращению аргумента  , когда
, когда  стремится к нулю, т.е.
стремится к нулю, т.е.
 .
.
Задание. Вычислите производную функции  в точке
в точке  , если:
, если:
а)  ; б)
; б)  .
.
| № | План вычисления производной | Применение | плана |
| шага | функции | а)  | б)  |
Фиксируем точку x и даем аргументу приращение  |  |  | |
Вычисляем приращение функции  |     |   | |
Находим отношение приращения функции к приращению аргумента:  |   |  | |
Вычисляем производную  |   |     | |
Вычисляем  |  |  |
Пример2. Вычислите производные следующих функций:
1)  в точке
в точке  ; 2)
; 2)  в точке
в точке  ; 3)
; 3)  в точке
в точке  ; 4)
; 4)  в точке
в точке  ; 5)
; 5)  в точке
в точке  ; 6)
; 6)  в точке
в точке  ;
;
7)  в точке
в точке  ; 8)
; 8)  в точке
в точке  .
.
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ.
Вариант 1.
1. Найдите приращение функции f в точке  , если
, если  .
.
2. Найдите приращения  и
и  в точке
в точке  , если
, если  .
.
3. Найдите производную функции f в точке  по определению, если
по определению, если  при
при  = 1.
= 1.
4. Найдите мгновенную скорость точки, движущейся прямолинейно по закону  , в момент времени
, в момент времени  , если
, если  .
.
Вариант 2.
1. Найдите приращение функции f в точке  , если
, если  .
.
2. Найдите приращения  и
и  в точке
в точке  , если
, если  .
.
3. Найдите производную функции f в точке  по определению, если
по определению, если 
при  = 1.
= 1.
4. Найдите мгновенную скорость точки, движущейся прямолинейно по закону  , в момент времени
, в момент времени  , если
, если  .
.
Вариант 3.
1. Найдите приращение функции f в точке  , если
, если  .
.
2. Найдите приращения  и
и  в точке
в точке  , если
, если  .
.
3. Найдите производную функции f в точке  по определению, если
по определению, если  при
при  = 1.
= 1.
4. Найдите мгновенную скорость точки, движущейся прямолинейно по закону  , в момент времени
, в момент времени  , если
, если  .
.
Вариант 4.
1. Найдите приращение функции f в точке  , если
, если  .
.
2. Найдите приращения  и
и  в точке
в точке  , если
, если  .
.
3. Найдите производную функции f в точке  по определению, если
по определению, если  при
при  = 1.
= 1.
4. Найдите мгновенную скорость точки, движущейся прямолинейно по закону  , в момент времени
, в момент времени  , если
, если  .
.
ПРАКТИЧЕСКАЯ РАБОТА №2
«Вычисление производных алгебраических функций»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки в теме: «Вычисление производных алгебраических функций».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: таблица производных элементарных функций; микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Ответить на контрольные вопросы:
а) Сформулируйте определение функции.
б) Сформулируйте правила вычисления производных алгебраических функций.
в) В чем состоит механический смысл производной?
г) Тело движется по прямой согласно закону х(t). Запишите формулы для нахождения скорости и ускорения тела в момент времени t.
2. По образцу выполнить тренировочные задания.
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ
Вариант 1.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а)  ; б)
; б)  ; в)
; в)  .
.
2. Решите уравнение  , если
, если  .
.
Вариант 2.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а)  ; б)
; б)  ; в)
; в)  .
.
2. Решите неравенство  , если
, если  .
.
Вариант 3.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а)  ; б)
; б)  ; в)
; в)  .
.
2. Решите уравнение  , если
, если  .
.
Вариант 4.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а)  ; б)
; б)  ; в)
; в)  .
.
2. Решите уравнение  , если
, если  .
.
Вариант 5.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а)  ; б)
; б)  ; в)
; в)  .
.
2. Решите уравнение  , если
, если  .
.
Вариант 6.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а)  ; б)
; б)  ; в)
; в)  .
.
2. Материальная точка движется прямолинейно по закону  . Через сколько секунд после начала движения точка остановится?
. Через сколько секунд после начала движения точка остановится?
Вариант 7.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а)  ; б)
; б)  ; в)
; в)  .
.
2. Найдите х, при котором  , если
, если  .
.
Вариант 8.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а)  ; б)
; б)  ; в)
; в)  .
.
2. По прямой движутся две материальные точки по законам  и
и  . В каком промежутке времени скорость первой точки больше скорости второй?
. В каком промежутке времени скорость первой точки больше скорости второй?
ПРАКТИЧЕСКАЯ РАБОТА №3
«Вычисление производных сложных функций»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки в теме: «Вычисление производных сложных функций».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: таблица производных элементарных функций; микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Ответить на контрольные вопросы:
а) Какая функция называется сложной? Приведите примеры сложных функций.
б) Сформулируйте правило вычисления производной сложной функции.
2. По образцу выполнить тренировочные задания.
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ
Вариант 1.
Вычислите производные сложных функций:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  .
.
Вариант 2.
Вычислите производные сложных функций:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  .
.
Вариант 3.
Вычислите производные сложных функций:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  .
.
Вариант 4.
Вычислите производные сложных функций:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  .
.
Вариант 5.
Вычислите производные сложных функций:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
Вариант 6.
Вычислите производные сложных функций:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  .
.
Вариант7.
Вычислите производные сложных функций:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ;
;
Вариант 8.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  .
.
ПРАКТИЧЕСКАЯ РАБОТА №4
«Нахождение наибольшего и наименьшего значений функции»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки в теме: «Наибольшее и наименьшее значения функции на отрезке. Решение прикладных экстремальных задач».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности учащихся.
ОБОРУДОВАНИЕ: таблицы производных элементарных функций, микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Ответить на контрольные вопросы:
а) Какую точку называют критической точкой функции?
б) Сформулируйте признак возрастания (убывания) функции.
в) Сформулируйте признак максимума (минимума) функции.
г) Опишите схему исследования функции.
2. С помощью обучающих таблиц повторить планы нахождения наибольшего и наименьшего значений функции на отрезке, решения прикладных экстремальных задач и изучить образцы решенных примеров.
3. Выполнить задания для самоконтроля (в таблице).
ОБУЧАЮЩИЕ ТАБЛИЦЫ
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ.
Вариант 1.
1. Найдите наибольшее и наименьшее значения функции 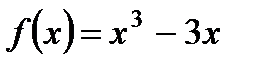 на отрезке
на отрезке 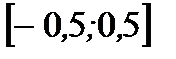 .
.
2. Из квадратного листа жести со стороной 12 м надо изготовить бак с квадратным основанием без крышки наибольшего объема. Найдите размеры бака и его объем.
Вариант 2.
1. Найдите наибольшее и наименьшее значения функции 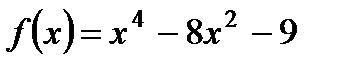 на отрезке
на отрезке 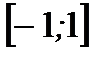 .
.
2. Какой из прямоугольников с периметром 2pимеет наибольшую площадь?
Вариант 3.
1. Найдите наибольшее и наименьшее значения функции 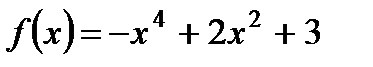 на отрезке
на отрезке 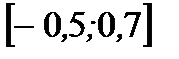 .
.
2. Разность двух чисел равна 8. Каковы должны быть эти числа. Чтобы произведение куба первого числа на второе было наименьшим?
Вариант 4.
1. Найдите наибольшее и наименьшее значения функции 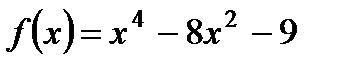 на отрезке
на отрезке 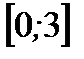 .
.
2. Для стоянки машин выделили площадку прямоугольной формы, примыкающую одной стороной к стене здания. Площадку обнесли с трех сторон металлической сеткой длиной 200 м. И площадь ее при этом оказалась наибольшей. Каковы размеры площадки?
Вариант 5.
1. Найдите наибольшее и наименьшее значения функции 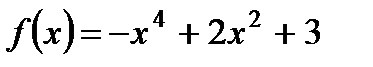 на отрезке
на отрезке 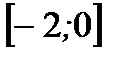 .
.
2. Из куска картона 32 см  20 см требуется изготовить открытую сверху коробку наибольшей вместимости, вырезая по углам квадраты и затем, загибая выступы для образования боковых сторон коробки. Найдите объем коробки.
20 см требуется изготовить открытую сверху коробку наибольшей вместимости, вырезая по углам квадраты и затем, загибая выступы для образования боковых сторон коробки. Найдите объем коробки.
Вариант 6.
1. Найдите наибольшее и наименьшее значения функции 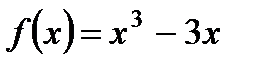 на отрезке
на отрезке 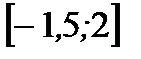 .
.
2. Требуется сделать коробку, объем которой должен равняться 108 см 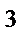 . Коробка открыта сверху и имеет квадратное дно. Каковы должны быть ее размеры, чтобы на ее изготовление пошло наименьшее количество материала?
. Коробка открыта сверху и имеет квадратное дно. Каковы должны быть ее размеры, чтобы на ее изготовление пошло наименьшее количество материала?
Вариант 7.
1. Найдите наибольшее и наименьшее значения функции 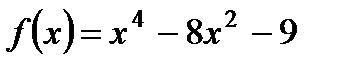 на отрезке
на отрезке 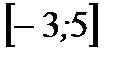 .
.
2. На странице книги печатный текст должен занимать (вместе с промежутками между строк)
160 см 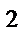 . Ширина полей на странице слева и справа должна быть равна 2 см, а сверху и снизу – 5 см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?
. Ширина полей на странице слева и справа должна быть равна 2 см, а сверху и снизу – 5 см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?
Вариант 8.
1. Найдите наибольшее и наименьшее значения функции 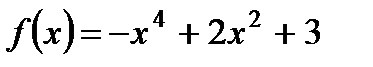 на отрезке
на отрезке 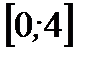 .
.
2. Материальная точка совершает прямолинейное движение по закону 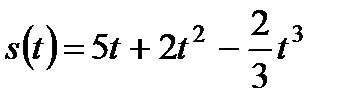 , где t – время в секундах, s – путь в метрах. В какой момент времени t скорость движения точки будет наибольшей и какова величина этой наибольшей скорости?
, где t – время в секундах, s – путь в метрах. В какой момент времени t скорость движения точки будет наибольшей и какова величина этой наибольшей скорости?
ПРАКТИЧЕСКАЯ РАБОТА №5
«Свойства функций»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки в теме: «Свойства функций».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Ответить на контрольные вопросы:
а) Что называется функцией?
б) Что такое естественная область определения функции?
в) Какая функция называется четной, нечетной?
г) Как найти точки пересечения графика функции с осями координат?
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ
Вариант 1.
1. Найдите 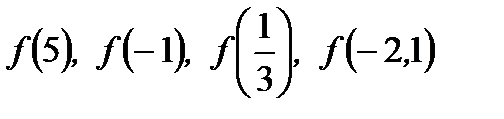 , если
, если 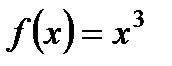 .
.
2. Найдите область определения функции 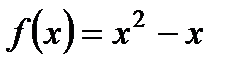 .
.
3. Установите, является ли функция 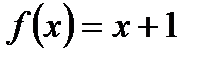 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 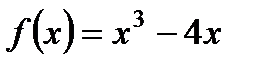 с осью ОУ и нули функции.
с осью ОУ и нули функции.
Вариант 2.
1. Найдите 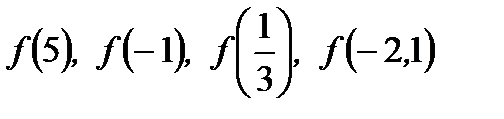 , если
, если 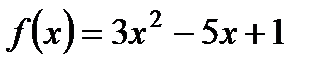 .
.
2. Найдите область определения функции 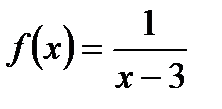 .
.
3. Установите, является ли функция 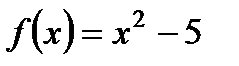 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 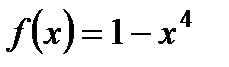 с осью ОУ и нули функции.
с осью ОУ и нули функции.
Вариант 3.
1. Найдите 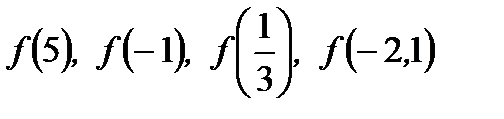 , если
, если 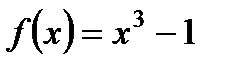 .
.
2. Найдите область определения функции 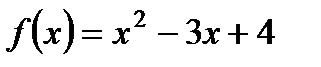 .
.
3. Установите, является ли функция 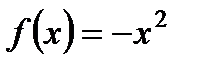 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 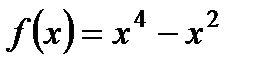 с осью ОУ и нули функции.
с осью ОУ и нули функции.
Вариант 4.
1. Найдите 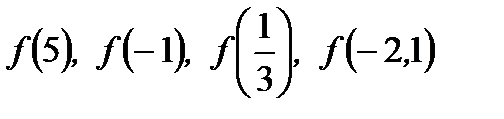 , если
, если 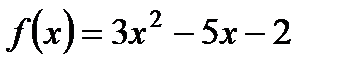 .
.
2. Найдите область определения функции 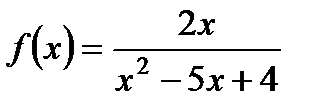 .
.
3. Установите, является ли функция 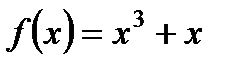 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 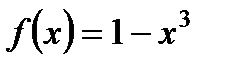 с осью ОУ и нули функции.
с осью ОУ и нули функции.
Вариант 5.
1. Найдите 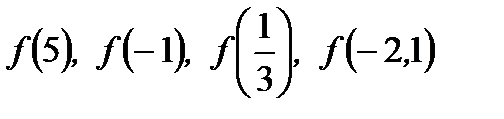 , если
, если 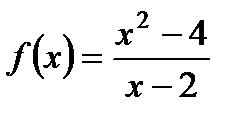 .
.
2. Найдите область определения функции 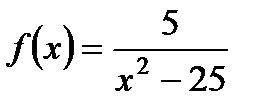 .
.
3. Установите, является ли функция 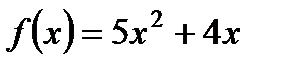 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 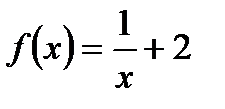 с осью ОУ и нули функции.
с осью ОУ и нули функции.
Вариант 6.
1. Найдите 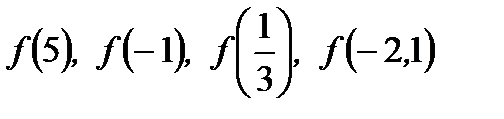 , если
, если 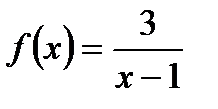 .
.
2. Найдите область определения функции 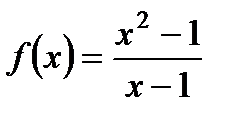 .
.
3. Установите, является ли функция 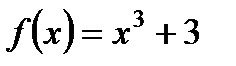 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 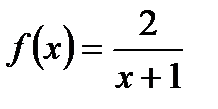 с осью ОУ и нули функции.
с осью ОУ и нули функции.
Вариант 7.
1. Найдите 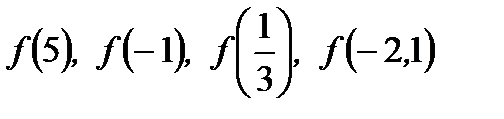 , если
, если 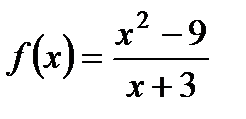 .
.
2. Найдите область определения функции 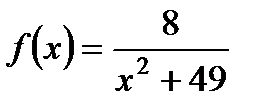 .
.
3. Установите, является ли функция 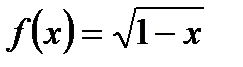 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 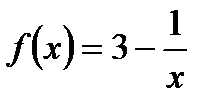 с осью ОУ и нули функции.
с осью ОУ и нули функции.
Вариант 8.
1. Найдите 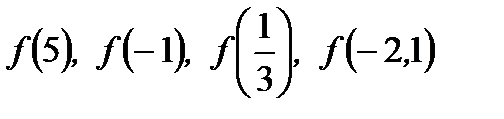 , если
, если 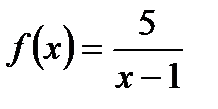 .
.
2. Найдите область определения функции 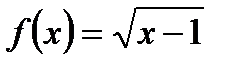 .
.
3. Установите, является ли функция 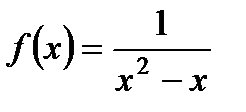 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 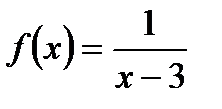 с осью ОУ и нули функции.
с осью ОУ и нули функции.
ПРАКТИЧЕСКАЯ РАБОТА №6
«Исследование функции и построение ее графика»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки в теме: «Исследование функции и построение ее графика».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: таблицы производных элементарных функций, микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Ответить на контрольные вопросы:
а) Какую точку называют критической (стационарной) точкой функции?
б) Сформулируйте признак возрастания (убывания) функции.
в) Сформулируйте признак максимума (минимума) функции.
г) Опишите схему исследования функции.
2. С помощью обучающей таблицы повторить план исследования функции и изучить образцы решенных примеров.
3. Выполнить задания для самоконтроля (в таблице).
ОБУЧАЮЩАЯ ТАБЛИЦА
Задание. Исследуйте и постройте графики функции:
а) 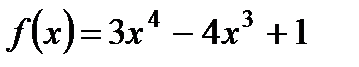 ;б)
;б) 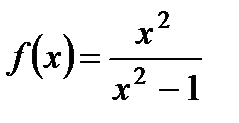 .
.
| № | План исследования | Применение | плана | ||
| шага | Функции | а)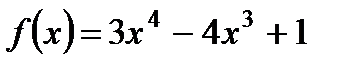 | б) 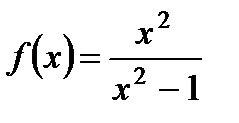 | ||
| Находим область определения функции | 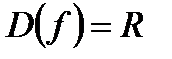 | 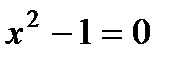 , , 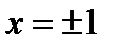 , , 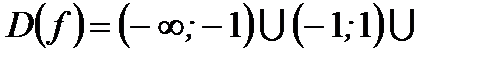 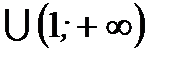 | |||
| Исследуем функцию на четность, нечетность | 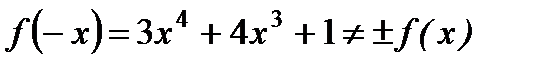  функция ни четная, ни нечетная функция ни четная, ни нечетная | 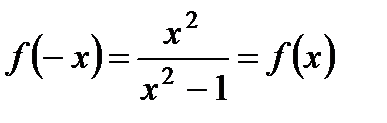 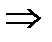 функция четная функция четная | |||
| Находим нули (корни) функции и промежутки её знакопостоянства | 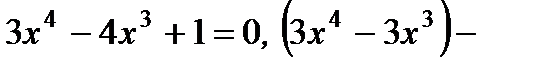 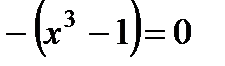 , , 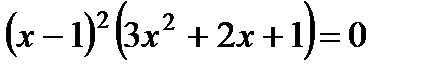 , , 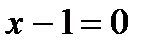 , , 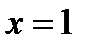 - нуль функции - нуль функции | 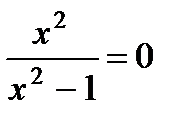 , , 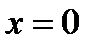 - нуль функции - нуль функции | ||
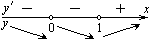
| Находим производную функции и её критические точки | 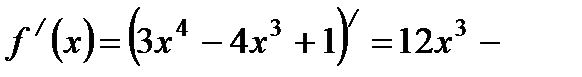 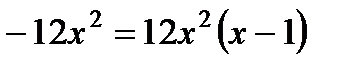 , , 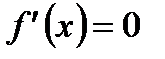 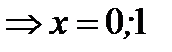 - критические точки функции - критические точки функции | 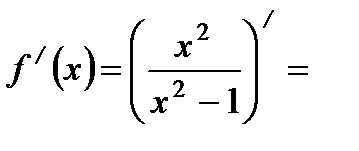 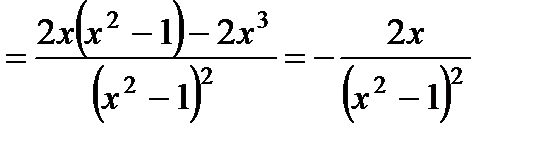 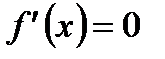 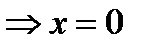 - критическая точка функции - критическая точка функции | |||
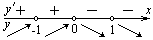
| Находим промежутки монотонности, точки экстремума и экстремумы функции | 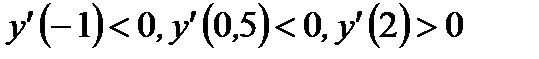 х=0 – не является точкой экстремума, х=1 – точка минимума, х=0 – не является точкой экстремума, х=1 – точка минимума, 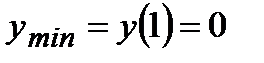 | 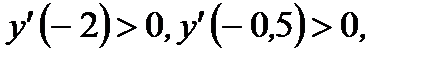 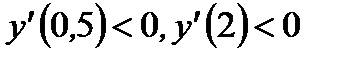 , х=0 – точка максимума, , х=0 – точка максимума, 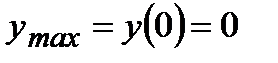 | ||
Находим предел функции при 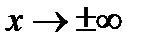 | 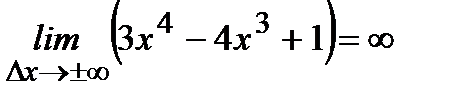 | 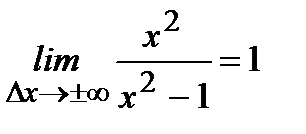 | |||
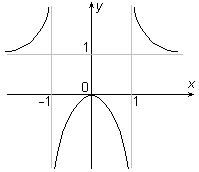
| Строим эскиз графика функции |
Примеры. Исследуйте и постройте графики функций:
1) 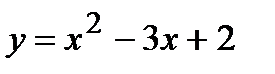 ; 2)
; 2) 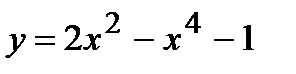 ; 3)
; 3) 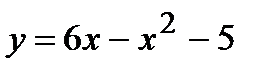 ; 4)
; 4) 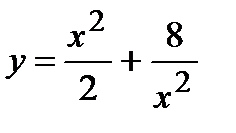 ; 5)
; 5) 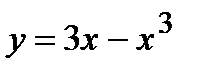 ; 6)
; 6) 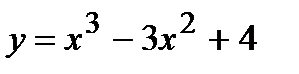 ; 7)
; 7) 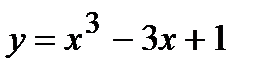 ; 8)
; 8) 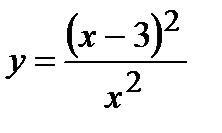 ; 9)
; 9) 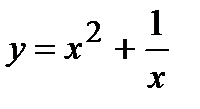 .
.
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ.
Вариант 1.
1. Исследуйте функцию 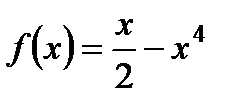 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 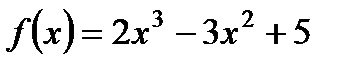 и постройте ее график.
и постройте ее график.
Вариант 2.
1. Исследуйте функцию 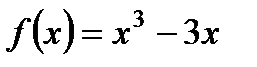 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 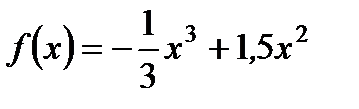 и постройте ее график.
и постройте ее график.
Вариант 3.
1. Исследуйте функцию 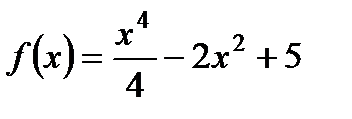 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 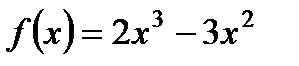 и постройте ее график.
и постройте ее график.
Вариант 4.
1. Исследуйте функцию 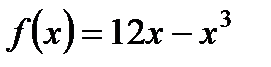 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 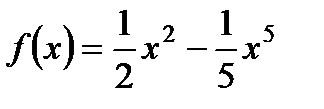 и постройте ее график.
и постройте ее график.
Вариант 5.
1. Исследуйте функцию 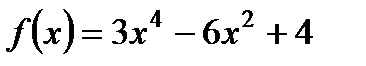 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 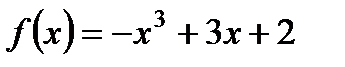 и постройте ее график.
и постройте ее график.
Вариант 6.
1. Исследуйте функцию 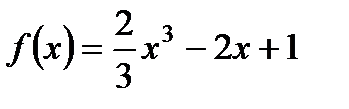 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 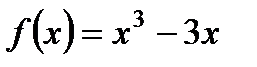 и постройте ее график.
и постройте ее график.
Вариант 7.
1. Исследуйте функцию 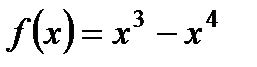 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 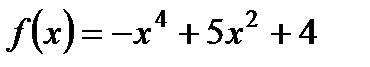 и постройте ее график.
и постройте ее график.
Вариант 8.
1. Исследуйте функцию 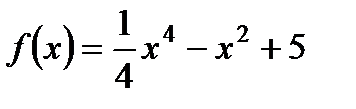 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 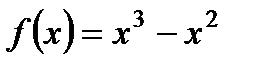 и постройте ее график.
и постройте ее график.
ПРАКТИЧЕСКАЯ РАБОТА №7
ПРАКТИЧЕСКАЯ РАБОТА №8
«Вычисление первообразных функций»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки в теме: «Вычисление первообразной функции».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: таблицы первообразных некоторых функций, микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Ответить на контрольные вопросы:
а) Что называется первообразной функции?
б) Сформулируйте основное свойство первообразной.
в) Сформулируйте три правила нахождения первообразных.
2. Изучить образцы решенных примеров.
3. Выполнить задания для самоконтроля.
ПРАКТИЧЕСКАЯ РАБОТА №9
«Вычисление определенного интеграла»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки в теме: «Вычисление определенного интеграла».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: таблицы первообразных некоторых функций, микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Ответить на контрольные вопросы:
а) Что называется первообразной функции?
б) Сформулируйте основное свойство первообразной.
в) Сформулируйте три правила нахождения первообразных.
г) Запишите формулу Ньютона-Лейбница.
2. Изучить образцы решенных примеров.
3. Выполнить задания для самоконтроля.
ПРАКТИЧЕСКАЯ РАБОТА №10
«Применение интеграла для вычисления площадей и объемов»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки в теме: «Применение определенного интеграла для вычисления площадей и объемов».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат д