Возрастание и убывание функций. Точки экстремума функции.
Определение1 Функция y=f(x) наз. возрастающей в интервале (а,в), если для любого Х1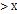 
2, где Х1,Х2 
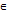(а,в), выполняется условие f(X1) 
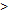f(X2).
Определение2 Функция y=f(x) наз. убывающей в интервале (а,в), если для любого Х1 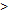Х2, где Х1,Х2 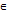(а,в) выполняется след. условие f(X1) 
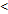f(X2).
Возрастание или убывание в некотором интервале (а,в), функция наз. монотонной в этом интервале.
Теорема1 Если ф-ция y=f(x) дифференцирован в интервале (а,в) и f'(x) 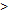0 при всех Х 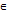(а,в), то функция f(x) 
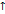в интервале (а,в), но если f’(x)<0 при всех Х 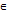(а,в), то ф-ция f(x) 
в интервале(а,в).
Определение3 Точка Х0 наз. min функции y=f(x), если существует такая -окрестность V(X0,v) точки Х0 что для любого Х 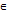V(X0,v) выполняется неравенство f(x0)<f(x). Если же для любого х 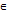V(X0,v) выполняется неравенство f(x0) >f(x), то точка Х0 наз. точкой max.
При этом число f(X0) наз. min(max) функции. Точки min(max) наз. её точками экстремума.
Теорема2Если функция y = f(x)в точке x0имеет экстремуму, то f’(x)=0 или f’(x) не существует.
Теорема3 Пусть функция y = f(x) дифференцирова в некоторой v - окресностиV(x0,v)=(x0-v, x0+v) точки X0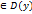 
за исключением могут быть самой точки Х0. Если f’(x)>0 для любого x 
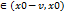и f’(x)<0 для любого х 
.
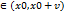Теорема4Пустьf’(x0)=0 илиf”(x0) 
. Тогда функцияy = f(x) имеет в точке Х0max, если f”(x0)<0 и min, если f”(x0)>0.
Наименьшее и наибольшее значения функции на отрезке.
Алгоритм нахождения наименьшего и наибольшего значений функции на отрезке (а,в):
1. найти критические точки функции, оставить для рассмотрения только те из них, которые на интервале (а,в)
2. вычислить значения функции в найденных критических точках
3. вычислить значения функции на концах отрезка при х=а и х=в
4.среди всех вычисленных значений функции выбрать наименьшее и наибольшее
Выпуклость и вогнутость графика функции. Точки перегиба.
Определение 1. График дифференциальной функции y=f(x) наз. выпуклым в интервале (а,в), если он расположен ниже любой её касательной на этом интервале. График дифференциальной функции y=f(x) наз. вогнутым в интервале (а,в), если он расположен выше ниже любой её касательной на этом интервале.
Определение 2. Точка (Х0, f(X0), Х0 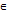D(y) графика непрерывной ф-цииy=f(x), отделяя её выпуклую(вогнутую) часть от вогнутой(выпуклой) наз. её точкой перегиба.
Асимптоты графика функции.
Определение.ПрямаяL наз. асимптотойкривой y=f(x), если расстояние от точки M(x,y) кривой до прямой L стремится к нулю при неограниченном удалении этой точки по кривой от точки O(0;0) (т.е. при стремлении хотя бы одной из координат точки к ¥).
Асимптоты бывают вертикальные и невертикальные (наклонные и горизонтальные).
Утверждение 1. Прямая x=a явл. вертикальной асимптотой графика функции y=f(x), если
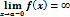
или
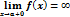
Т.е. для отыскания вертикальных асимптот нужно найти те значенияx, вблизи которых функция f(x) неограниченно возрастает по модулю.
Замечание 1. Если
D(y)={(-¥;+¥) или [a;b] или (-¥;b] или [a;+¥)}, то вертикальных асимптот нет.
Замечание 2. Если
D(y)=(-¥;x1)È(x1;x2)È…È(xn;+¥), то вертикальные асимптоты могут быть только прямые.
x=xi, i=1,…,n
(если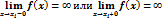 
).
Замечание 3.Если D(y)=(a;+¥), то вертикальная асимптотой может быть только прямая x=a (если
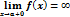
Замечание 4.Если D(y)=(-¥;b), то вертикальной асимптотой может быть только прямая x=b (если
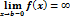
Утверждение 2. Если
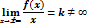
и
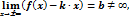
то y=kx+b – невертикальная асимптота. Причем k¹0 – наклонная, а при k=0 – горизонтальная асимптота.