Смешанное произведение векторов. Свойства смешанного произведения и его вычисление в ортонормированном базисе.

Смешанными векторами а, в, с наз. число обозначаемое а, в, с и определяемое как скалярное произведение вектора ā×в×с :авс= (ā×в)×с.

Свойства:

1)смешанное произведение не меняется при цикле пересечения его вектора со множителем: авс=вса=сав

2)смешанное произведение меняет знак на противоположный при перестановке любых векторов множителей: авс=-вас=вса

3)смешанные произведения не меняются при перемене местами знаков векторного и скалярного умножения :(ā×в)*с=ā*(в×с)

4)смешанные произведения не нулевых векторов равно 0 тогда и только тогда, когда векторы комплонарны : авс=0 óавс-комплонарны.

Приложения смешанного произведения.

1)определение взаимной ориентации вектора в пространстве: если авс>0 => векторы а, в, с образуют правую тройку, если авс<0, то левую тройку.

2)установление комплонарности вектора. Векторы а, в, с – комплонарныóавс=0.

3)определение объёмов в пространстве предметов: а)V- парал-да, построенного на векторах а, в, с вычисляются по формуле :V=/abc/

б)V=1/6*/abc/

в)V треугольной призмы, построенный на векторах а, в, с вычисляется по формуле: V=1/2*/abc/

Различные виды уравнений прямой на плоскости: по точке и нормальному вектору; общее; по точке и направляющему вектору; по двум точкам; по точке и угловому коэффициенту; в отрезках.

1.по точке и нормальному векторуА(х – х₀) + В(у – у₀)=0

2.общее уравнение Ах + Ву + (- Ах₀ – Ву₀) = 0 или Ах + Ву + С =0

3.по точке и направляющему вектору М₀М║S =>М₀М=t*S х-х0/m=y-y₀/n

4.по двум точкам х-х1/х2-х1=у-у1/у2-у1

5.по точке и угловому коэффициенту y-y₀ = k(x-x₀)y=kx + b

6. в отрезках х/а+у/в=1

Расстояние от точки до прямой.

d= /Ax₀+By₀+C/ 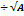²+B²

Различные виды уравнений плоскости в пространстве: по точке и направляющему вектору; общее; по трём точкам; в отрезках.

1) А(х-х₀)+В(у-у₀)+С(z-z₀=0(по точке и напр. вектору);

2) Ах+Ву+Cz+(-Ax₀-By₀-Cz₀)=0илиАх+Ву+Cz+D=0(общее уравнение);

3) 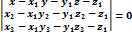(по трём точкам)

4) 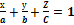(уравнениеплоскостив отрезках).

Взаимное расположение двух плоскостей в пространстве.

Случаи взаимного расположения плоскостей:

1) Р1 ║ Р2 ó А1/А2=В1/В2=С1/С2≠Д1/Д2

2) Р1 совпадает с Р2 ó А1/А2=В1/В2=С1/С2=Д1/Д2

3) Р1 ┴ Р2 ón1*n2=0 ó А1А2+В1В2+С1С2=0

4) Р1 пересекает Р2 под углом γ ócos γ = n1*n2 /n1/*/n2/=A1A2+B1B2+C1C2 *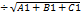

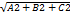
Различные виды уравнений прямой в пространстве: общее; по точке и направляющему вектору; по двум точкам

1)

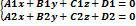
2) = =

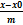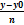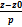
3)

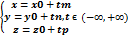
4) = =

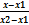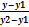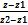
Понятие функции. Основные характеристики функции: чётная, нечётная, возрастающая, убывающая, ограниченная.

Пусть дано 2 не пустых множества Х и У. Правило f по которому каждый элемент Х 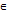Х поставлен в соответствие 1 и только 1 элементa У 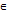У, наз. функцией и записывается : у=f(x).

Основные характеристики:

1)Функция у=f(x) , определяемая на множестве D, наз. чётной, если любая Х 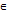D выполняет условия : -х 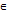D и f(-x)=f(x); не чётной , если любая Х 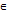D и f(-x)=-f(x)

2)Функция y=f(x) наз. возрастающей на интервале (а,в), если любое X1,X2 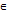(а,в) Х1>X2, выполняется f(x1)>f(x2). Функция наз. убывающей если любое х1 и х2 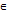(а,в) Х1>X2, выполняется условие f(x1)<f(x2).

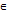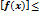3) Функцию y = f(x) опр. на множество D, наз. ограниченной на этом множестве, если сущ. Такое число М>0: любое х D => M