Согласованные матрицы. Умножение матриц и его свойства.
Матрицы и их виды.
Матрица размером m*n –совокупность m*n чисел расположенных в виде таблицы.Из m-строк и n-столбцов.
- Матрица, все элементы, которой равны нулю наз. нулевой.
- Матрица, у которой число строк равно числу столбцов наз. квадратной.
- Квадратная матрица, у которой все элементы, кроме элемента главной диагонали равны нулю, наз. диагональной.
Диагональная матрица у которой каждый элемент =1, наз. единичной.
2.Сложение матриц и умножение на действительное число.
- сложение матриц: суммой(разностью) матрицы Am*n,=(aij) и Bm*n=(bij) наз. такая матрица Сm*n, что cij=aij±bij
- умножение: произведение Am*n=(aij)наk, наз. Число bBm*n = (bij), bij=k*aij.
Согласованные матрицы. Умножение матриц и его свойства.
| Операции сложения матриц и умножения на число .Свойства. |
| А+ В = В + А |
| (А+В) + С= А(В+С) |
| А+0 = А |
| А-А = 0 |
| Α * (А+В) = α*В + α*А |
| 1*А = А |
| (α+β)*А = α*А + β*В |
| α(β*А) = (α*β)*А |
4.Элементарные преобразования матриц. Эквивалентные матрицы.
Элементарными преобразованиями матриц, явл.:
1)перестановка двух параллельных рядов матрицы
2)умножение всех элементов, любого ряда матрицы на отличное от нуля число
3)прибавление ко всем элементам ряда матриц соответствующих элемент.параллельного ряда и умноженное на одно и тоже число.
Две матрицы называются эквивалентными, если 1 из них получается из другой с помощью элементарных преобразований и обозначается А˜ В.
Определители 2-гопорядка.
n=2, A2x2= 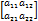 , det A=
, det A= 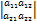 =a11× a22 – a12×a21
=a11× a22 – a12×a21
Определители 3-го порядка.
n=3, A= 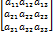 ,
,
det A= 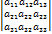 =a11× a22× a33+a21× a32× a13+a12× a23× a31- a13× a22× a31- a21× a12× a33- a32× a23× a11
=a11× a22× a33+a21× a32× a13+a12× a23× a31- a13× a22× a31- a21× a12× a33- a32× a23× a11
Миноры и алгебраические дополнение элемента определителя.
Минором элемента aijопределителя порядка n называется определитель n-1-го порядка, полученный из исходного вычеркивания i-ой строки j-го столбца.
Алгебраическим дополнением элемента aijс определителем ∆наз. Соответствующие минором взятом i+j-числа, «+» если i+j-четна, «-» если i+j-нечетна.
Свойства определителей.
Свойства:
1)Определитель не изменится, если его строки заменить соответствующими столбцами и наоборот.
2)Если поменять местами два параллельных ряда определителя, то определитель изменит знак.
3)Определитель с двумя одинаковыми параллельными рядами равен 0.
4)Общий множитель, какого – либо ряда можно вынести за знак определителя.
5)Определитель, у которого элементы двух рядов соответственно пропорционален, то он =0.
6)Если все элементы какого-либо ряда определителя равны 0, то и сам определитель равен 0.
7)Определитель не изменится, если к элементам одного ряда прибавить соответственно элементы другого параллельного ряда, умножить на одно и то же число.
8)Определитель равен сумме произведения элементов любого ряда на их алгебраическое дополнение.
Свойства обратной матрицы.
Свойства:
1) det (A-1) =1/detA
2) (AB)-1=A-1×B-1
3) (A-1)T=(AT)-1
Решение невырожденных систем линейных уравнений. Матричный метод. ФормулаКрамера. Метод Гаусса.
Матричный метод
Записать систему в матричном виде АХ=В. Умножим обе части последнего матричного уравнения слева на матрицу А-1.Поскольку А-1×А = Е и ЕХ=Х, то формула для нахождения столбца их неизвестных примет вид: Х = А-1×В
Формула Крамера
Введём следующие обозначения:
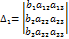 ,
, 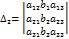 ,
, 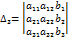
т.е. определители ∆1, ∆2, ∆3, получаются из определителя ∆ путём замены его 1,2 и 3 столбцов соответственно столбцом свободных членов, тогда единственное решение системы может быть найдена по формуле Крамера: х1=∆1/∆, х2=∆2/∆, х3=∆3/∆.
Метод Гауса
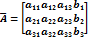
С помощью элементарных преобразований над строками приведём матрицу к трапецеидальному виду:
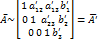
Далее запишем систему линейных уравнений, которая соответствует расширенной матрице А :
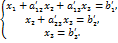
из которых последовательно и найдём искомое решение.
Теорема Кронекера-Капелли
Для того, чтобы система была совместной , необходимо и достаточно, чтобы ранг матрицы А был равен рангу её расширенной матрицы Ā. Если ранг матрицы А= рангу матрицы Ā и равен числу неизвестных, то система имеет единственное решение. Если ранг матрицы А = рангу матрицы Ā, но меньше числа неизвестных то система имеет бесконечное множество решений.
Проекция вектора на ось.
Осьюназ. всякая прямая, на которой указано направление.
Проекцией точки М на ось наз. основание перпендикуляра, опущенного из точки М на данную ось.
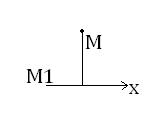
Углом между вектором ĀВ или равным ему вектором СВ и осью Ох наз. угол α, на который нужно повернуть кратчайшем образом полуось Ох, до совмещения её с вектором СВ.
Область изменения угла α: 0≤α≤π.
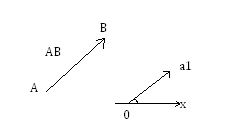
Проекцией вектора АВ на ось Ох наз. число, обозначаемое прОхАВ и /АВ/*cosα, где α- это угол между вектором Ав и осью Ох, т.е. по определению:
ПРОхАВ = /АВ/ * cosα
Геометрическая проекция вектора АВ на ось Ох = длине отрезка СД, взятой со знаком +, если 0≤α≤π/2 и со знаком минус , если π/2<α≤π. При α=π/2 отрезок СД превращается в точку и ПРОХ АВ = 0.
Свойства:
1.при умножении вектора АВ на число m, его проекция на ось умножается на то же число: прохАВ*m = m*прохАВ
2.проекция суммы двух векторов на ось, равна сумме проекции, соответствующих на ту же ось: прох(АВ + СД) = прохАВ + прохСД
Тригонометрические функции
а) у = sinx
б) y = cosx
в) y = tgx
г) y = ctg x
Правила дифференцирования.
Теорема1. (u  v)’ = u’
v)’ = u’  v’.
v’.
Теорема2.(u * v)’ = u’v + uv’
Теорема3.(  )‘ = u’v – uv’ / v2 , v
)‘ = u’v – uv’ / v2 , v 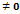
Правило Лопиталя.
Пусть функция f(x) и g(x) дифференцированны в окрестные точки Х0 и g’(x) 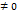 .
.
Если 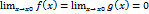
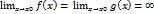 , т.е. частное f(x)/g(x) представляет собой неопределённость вида 0/0 или
, т.е. частное f(x)/g(x) представляет собой неопределённость вида 0/0 или 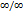 , то
, то 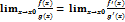 при условии что существует.
при условии что существует.
Замечание1. 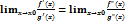
Замечание2.Неопределённость вида 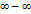 приводится к неопределённому пределу
приводится к неопределённому пределу  , а неопред. вида 0
, а неопред. вида 0 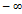 к неопред. виду
к неопред. виду  или
или  путём алгебраических преобразований исследования функции.
путём алгебраических преобразований исследования функции.
Асимптоты графика функции.
Определение.ПрямаяL наз. асимптотойкривой y=f(x), если расстояние от точки M(x,y) кривой до прямой L стремится к нулю при неограниченном удалении этой точки по кривой от точки O(0;0) (т.е. при стремлении хотя бы одной из координат точки к ¥).
Асимптоты бывают вертикальные и невертикальные (наклонные и горизонтальные).
Утверждение 1. Прямая x=a явл. вертикальной асимптотой графика функции y=f(x), если
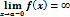
или
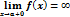
Т.е. для отыскания вертикальных асимптот нужно найти те значенияx, вблизи которых функция f(x) неограниченно возрастает по модулю.
Замечание 1. Если
D(y)={(-¥;+¥) или [a;b] или (-¥;b] или [a;+¥)}, то вертикальных асимптот нет.
Замечание 2. Если
D(y)=(-¥;x1)È(x1;x2)È…È(xn;+¥), то вертикальные асимптоты могут быть только прямые.
x=xi, i=1,…,n
(если 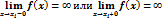 ).
).
Замечание 3.Если D(y)=(a;+¥), то вертикальная асимптотой может быть только прямая x=a (если
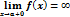
Замечание 4.Если D(y)=(-¥;b), то вертикальной асимптотой может быть только прямая x=b (если
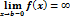
Утверждение 2. Если
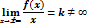
и
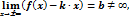
то y=kx+b – невертикальная асимптота. Причем k¹0 – наклонная, а при k=0 – горизонтальная асимптота.
Первообразная функции. Неопределённый интеграл и его свойства. Таблица основных неопределённых интегралов.
Определение1. Функция F(x) наз. первообразной функции f(x), заданной на некотором множестве Х, если для любого х 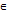 Х выполняется равенство: F'(x)=f(x).
Х выполняется равенство: F'(x)=f(x).
Определение2. Множество F(x) + C всех первообразной функции f(x) на множестве Х наз. неопределённым интегралом и обозначается: 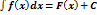
Нахождение первообразной для данной функции f(x) наз. интегрированием функции f(x).
Теорема.Для всякой непрерывной на интервале (а,в) функции f(x) существует на этом промежутке первообразная, а значит и неопределённый интеграл.
Геометрический неопределённый интеграл представляет собой семейство кривых, зависимых от одного параметра С, который получает одна из другой путём параллельного сдвига вдоль оси Оу.
Свойства:
1)( 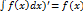
2) 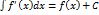
3) 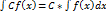
4) 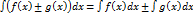
5)Если 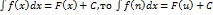
6)Если 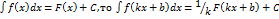
Таблица основных неопределённых интегралов:
1. 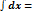 x + C x + C | 6. 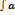 x dx = ax / ln a +C x dx = ax / ln a +C | 11. 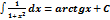 |
2. 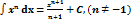 | 7. 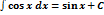 | 12. 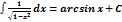 |
3. 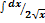 = = 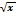 + C + C | 8. 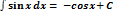 | 13. 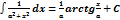 |
4. 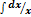 = ln = ln 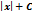 | 9. 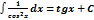 | 14. 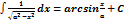 |
5. 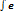 x dx = ex +C x dx = ex +C | 10. 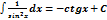 | 15. 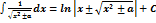 |
А/х-а
2) А/(х-а)к, (k³ 2, kÎN)
3) А/х2+рх+q, (D=p2-4q<0)
4)Ax+B/x2+px+q, (D=p2-4q<0)
5)Ax+B/(x2+px+q)k, (k³ 2, kÎN, D=p2-4q<0)
где A, a, B, p, qÎR.
Уравнение вида
P(x,y)dx+Q(x,y)dy=0, (*)
наз.однородным,если P(x,y)иQ(x,y) –однородные функции одного измерения.
Уравнение вида
y’= f(x,y), (**)
наз. однородным, если функция f(x,y) является функцией нулевого измерения.
Замечание 2.
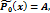
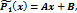
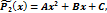
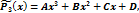 и т. д.,
и т. д.,
где A, B, C, D, … - неизвестные коэффициенты, которые находят подстановкой в уравнение (*)и приравниванием коэффициентов при одноимённых функциях в левой и правой частях равенства.
67. Понятие функции двух переменных. Область определения.
Пусть каждой упорядоченной паре чисел (х, у) из некоторой области D соответствует определённое число zÎEÌR. Тогда z=f(x, y)наз. функцией двух переменныхх и у, х, у – независимыми переменными или аргументами, D – областью определения, а множествоЕ всех значений функции – областью её значений. Геометрически область определения функции z=f(x, y) представляет собой либо всю плоскость Оху, либо некоторую часть плоскости Оху ограниченную линиями, которые могут принадлежать или не принадлежать этой плоскости.
Линию, ограничивающую область наз. границей области. Точки области, не лежащие на границе наз. внутренними. Область состоящая только из одних внутренних точек наз. открытой. Область с присоединённой к ней границей наз. замкнутой, и обозначается 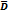 .
.
Матрицы и их виды.
Матрица размером m*n –совокупность m*n чисел расположенных в виде таблицы.Из m-строк и n-столбцов.
- Матрица, все элементы, которой равны нулю наз. нулевой.
- Матрица, у которой число строк равно числу столбцов наз. квадратной.
- Квадратная матрица, у которой все элементы, кроме элемента главной диагонали равны нулю, наз. диагональной.
Диагональная матрица у которой каждый элемент =1, наз. единичной.
2.Сложение матриц и умножение на действительное число.
- сложение матриц: суммой(разностью) матрицы Am*n,=(aij) и Bm*n=(bij) наз. такая матрица Сm*n, что cij=aij±bij
- умножение: произведение Am*n=(aij)наk, наз. Число bBm*n = (bij), bij=k*aij.
Согласованные матрицы. Умножение матриц и его свойства.
| Операции сложения матриц и умножения на число .Свойства. |
| А+ В = В + А |
| (А+В) + С= А(В+С) |
| А+0 = А |
| А-А = 0 |
| Α * (А+В) = α*В + α*А |
| 1*А = А |
| (α+β)*А = α*А + β*В |
| α(β*А) = (α*β)*А |
4.Элементарные преобразования матриц. Эквивалентные матрицы.
Элементарными преобразованиями матриц, явл.:
1)перестановка двух параллельных рядов матрицы
2)умножение всех элементов, любого ряда матрицы на отличное от нуля число
3)прибавление ко всем элементам ряда матриц соответствующих элемент.параллельного ряда и умноженное на одно и тоже число.
Две матрицы называются эквивалентными, если 1 из них получается из другой с помощью элементарных преобразований и обозначается А˜ В.
Определители 2-гопорядка.
n=2, A2x2= 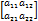 , det A=
, det A= 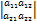 =a11× a22 – a12×a21
=a11× a22 – a12×a21
Определители 3-го порядка.
n=3, A= 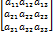 ,
,
det A= 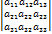 =a11× a22× a33+a21× a32× a13+a12× a23× a31- a13× a22× a31- a21× a12× a33- a32× a23× a11
=a11× a22× a33+a21× a32× a13+a12× a23× a31- a13× a22× a31- a21× a12× a33- a32× a23× a11
