Собственными называются колебания, которые совершает система около положения устойчивого равновесия после первоначального возмущения под действием только внутренних сил.

Какая сила должна действовать на систему, чтобы колебания были гармоническими? Так как для гармонических колебаний уравнение, связывающее ускорение и координату материальной точки выглядят как

а = - w²·х,

то согласно II закону Ньютона справедливо следующее равенство:

F = m·a = - m·w²·х = - k·x, (10.1)
где k - постоянная величина.

Итак, тело совершает гармонические колебания, если сила, возвращающая его в положение равновесия, пропорциональна смещению и направлена в противоположную этому смещению сторону.
Такая сила называется квазиупругой.

На практике зависимость F(x) является более сложной. Однако, при малых значениях величины х эту функцию можно разложить в ряд:

|F(x)| = k·x + k₁·x² + k₂·x³ + ...

и пренебречь слагаемыми более высокого, чем 1 порядка малости. Следовательно, любая система с одной степенью свободы при достаточно малом отклонении от положения равновесия будет гармонически колебаться.

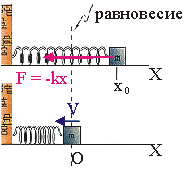
Рис. 10.1.

Уравнение динамики собственных колебаний. Рассмотрим колебания груза на пружине, считая, что вся масса сосредоточена в грузе, а упругость - в пружине. При х = 0 пружина не деформирована (см. рис. 10.1). Предположим, что сила трения в системе отсутствует F_тр = 0. В случае смещения тела от положения равновесия возникает сила упругости, действующая на тело и стремящаяся возвратить его в положение равновесия. Поскольку при малых деформациях х эта сила равна F = - k·x, то уравнение динамики движения груза согласно II закону Ньютона можно записать в виде:

m·a = - k·x. (10.2)

Поскольку ускорение - есть вторая производная от координаты по времени, то решив дифференциальное уравнение (10.2), найдем зависимость x(t). В теории дифференциальных уравнений показано, что общим решением уравнений типа x'' + w₀²·x = 0 выражается зависимостью вида: x = A·cos(w₀·t + f₀).

Можно рассуждать также следующим образом. Из (10.2) имеем, что для гармонических колебаний a = - w₀²·x, т.е. ускорение а пропорционально х и направлено в противоположную к нему сторону. Следовательно, колебания груза в случае выполнения условия (10.2) являются гармоническими и описываются уравнением:

x = A·cos(w₀·t + f₀), (10.3)
где w₀ = (k/m)^1/2 - собственная частота колебаний.

Значение w₀ зависит только от физических свойств системы и не зависит от начальных условий.

Расчет параметров собственных колебаний. Амплитуда A и начальная фаза f₀, называемые параметрами колебаний, не зависят от свойств системы, а определяются только начальными условиями, т.е. значением смещения и скорости в начальный момент времени:

x(0) = x₀; u(0) = u₀.

Задав x₀ и u₀, получим два уравнения для расчета амплитуды и начальной фазы:

x₀ = A·sin f₀; (10.4)
u₀ = A·w₀·cos f₀. (10.5)

Уравнения (10.4) и (10.5) задают значения A и f₀.

A = (x₀² + u₀²/w₀²)^1/2;
tg f₀ = x₀·w₀/u₀.

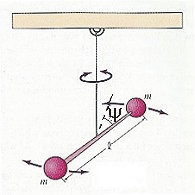
Рис. 10.2. Крутильные колебания.

Примеры собственных колебаний.
Крутильные колебания (см. рис. 10.2). Пусть y - угловая координата, I - момент инерции, K - модуль кручения. Уравнение динамики крутильных колебаний имеет вид:

I·e = - K·y или
y'' = - K·y/I. (10.6)

Сравнивая уравнения (10.6) и (10.1), видим, что они аналогичны. Следовательно, решение уравнения (10.6) имеет вид гармонической функции:

y(t) = y_max·sin((K/I)^1/2·t + f₀).

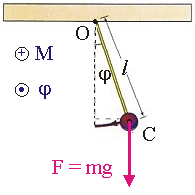
Рис. 10.3. Колебания физического маятника.

Физический маятник(см. рис. 10.3). Физическим маятником называется система, способная совершать колебания около положения равновесия, при этом массу системы нельзя считать сосредоточенной в одной точке. Введем обозначения: O - точка вращения; С - положение центра масс маятника; l - его длина; j - угол отклонения от положения равновесия. Уравнение динамики вращательного движения для физического маятника в проекции на ось вращения в случае его малых колебаний запишем в виде:

M_z = I·j'' = - m·g·l·sin j = - m·g·l·j.

Решение этого уравнения имеет следующий вид:

j(t) = j_max·sin(w₀·t + f₀),
где w₀ = (m·g·l/I)^1/2.

Для математического маятника момент инерции и значение собственной частоты колебаний будут равны:

I = m·l² и
w₀ = (g/l)^1/2.

Собственную частоту физического маятника можно представить в виде, аналогичном выражению для математического маятника:

w₀ = (g/l_прив)^1/2,
где l_прив = I/(m·l) - приведенная длина маятника.

Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону: 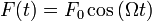.