Принцип суперпозиции. Сложение колебаний

Часто тело участвует в двух или нескольких колебаниях. Например, груз, подвешенный на пружине к потолку рессорного вагона, колеблется относительно точки подвеса, которая в свою очередь совершает колебания вместе с вагоном на его рессорах. Таким образом, груз будет совершать движение, складывающееся из двух колебаний. В таких случаях необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. По принципу суперпозиции эти колебания рассматриваются как независимые, и результирующее смещение находится в каждый момент времени как векторная сумма смещений отдельных колебаний. В случае сложения колебаний, направленных по одной прямой, результирующее смещение равно алгебраической сумме смещений отдельных колебаний.

При сложении колебаний можно пользоваться аналитическим, графическим методами и методом векторных диаграмм.

Сложим гармонические колебания одного направления и одинаковой частоты:

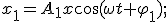
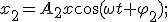
1. Аналитический метод. Результирующее смещение

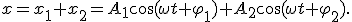
Покажем, что результирующее колебание также является гармоническим колебанием той же частоты, т.е. что

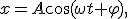
где А — амплитуда результирующего колебания; 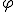— его начальная фаза. Тогда

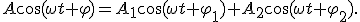
Используя формулу косинуса суммы двух углов, получим

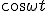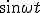Это уравнение будет тождеством относительно t, если коэффициенты при и в его левой части равны соответствующим коэффициентам в правой части в любой момент времени:

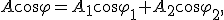
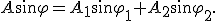
Решив эту систему уравнений, получим

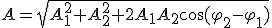
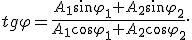
2. Графический метод. Сложение сводится к суммированию ординат в каждый момент времени (чем больше точек, тем точнее) — рисунок 13.6.

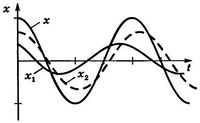
Рис. 13.6

3. Метод векторных диаграмм. Построим векторные диаграммы этих колебаний (рис. 13.7). Так как векторы 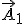и 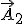вращаются с одинаковой угловой скоростью, то угол между ними, а значит, и разность фаз 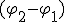составляющих колебаний, остаются постоянными. Результирующее смещение 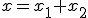, где х₁ + х₂ — сумма проекций векторов 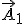и 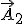на ось Ох. Из математики известно, что сумма проекций векторов равна проекции вектора суммы, т.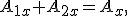е. где 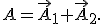Следовательно, амплитуда результирующего колебания равна модулю вектора 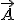. Из рисунка 13.7 видно, что по теореме косинусов

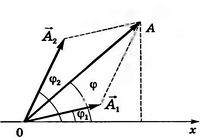
Рис. 13.7

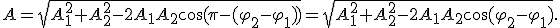
Угол наклона 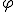вектора к оси Ох равен начальной фазе результирующего колебания. Из рисунка 13.7 видно, Таким образом, тело, участвуя в двух гармонических колебаниях одного что направления и одинаковой частоты, также совершает гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз 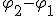При сложении гармонических колебаний одного направления, но разных частот, результирующее колебание не является гармоническим. Еще более сложными оказываются результирующие колебания, полученные при сложении колебаний, происходящих в разных направлениях.

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида 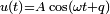в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний 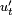или её квадрата.

В акустике: затухание — уменьшение уровня сигнала до полной неслышимости.