ЛПР, владелец проблемы, группа, члены группы, консультант, советники, эксперты.
ЛПР, владелец проблемы, группа, члены группы, консультант, советники, эксперты.
Варианты действий называют альтернативами.
Альтернативы бывают зависимые и независимые
Независимые– оценки альтернатив не зависят друг от друга
Зависимые– оценки альтернатив зависят друг от друга.
Варианты решений характеризуются различными показателями их привлекательности.Эти показатели называются признаками, атрибутами, критериями.
Сложность задачи зависит от числа критериев.
Для оценки критерия используются различные шкалы.
Числовые: порядковые, равных интервалов, пропорциональных оценок.
Лингвистические.
Общая концепция ТПР
Теория принятия решений представляет собой набор понятий и систематических методов, позволяющих всесторонне анализировать проблемы принятия решений в условиях неопределенности. Совершенствование процесса принятия решений - цель рассматриваемой теории.
В основе теории принятия решений лежит предположение о том, что выбор альтернатив должен определяться двумя факторами:
1) представлениями лица, принимающего решение о вероятностях различных возможных исходов (последствий), которые могут иметь место при выборе того или иного варианта решения;
2) предпочтениями, отдаваемыми им различным возможным исходам.
Оба фактора формально входят в теорию принятия решений, и чтобы их учесть требуется представить в виде цифр
а) суждения о возможных последствиях (опираясь на понятие субъективной вероятности) и
б) высказывания о предпочтениях (используя теорию полезности).
"Разделяй и властвуй" - вот девиз теории принятия решений. Согласно методике этой теории, рассматриваемую проблему необходимо разбить на части, которые следует изучить и анализировать отдельно, а затем построить общую модель для принятия решений.
Процесс принятия решений
Альтернативное решение – это один из вариантов достижения поставленной цели. Последствия применения альтернативы в качестве управляющего воздействия называются исходами.
Внешней средой называют совокупность всех внешних факторов, влияющих на исход решения, т.е. условия, в которых осуществляется ПР и которые необходимо учитывать при формализации и решении задачи.
Решающее правило формулируется на основе выявления системы предпочтения лица, принимающего решения.
Содержательно ЗПР формулируется так [29]: есть множество вариантов решения (альтернатив), реализация каждой из них приводит к наступлению некоторого исхода, анализ и оценка которого по показателям эффективности (критериям) точно характеризует альтернативу. Нужно, изучив предпочтение ЛПР, построить лучшую в некотором смысле модель выбора альтернативы.
Однако система предпочтений лица, принимающего решение слабо структурировано, т.е. не позволяет полностью проанализировать все альтернативы, установить их существенность, сформулировать критерии выбора наилучшей альтернативы. Поэтому необходимо провести определенную структуризацию задачи принятия решения позволяющий уточнить систему предпочтений лица, принимающего решение, а уже затем осуществить выбор [30].
Процесс принятия решений с технологической точки зрения можно представить в виде последовательности этапов и процедур имеющих между собой прямые и обратные связи. Обратные связи отражают итеративный циклический характер зависимости между этапами и процедурами. Итерации в выполнении элементов 'процесса принятия решений обусловлены необходимостью уточнения и корректировки данных после выполнения последующих процедур.
С информационной точки зрения в процессе принятия решений происходит уменьшение неопределенности. Формулировка проблемной ситуации как бы порождает вопрос «что делать?». Последовательное выполнение процедур приводит к формированию ответа на этот вопрос в виде «что и как нужно делать».
Процедуры принятия решений могут выполняться путем мышления ЛПР и экспертов, т. е. творчески, неформальным образом, и с применением формальных средств — математических методов и ЭВМ. В процессе принятия решений решается задача поиска, распознавания, классификации, упорядочения и выбора. Для решения этих задач используются методы анализа и синтеза, индукции и дедукции, сравнения и обобщения.
Формальные процедуры заключаются в проведении расчетов по определенным алгоритмам с целью анализа вариантов решения, оценки необходимых ресурсов, сужения множества вариантов решения и т. п. Выполнение формальных процедур осуществляется ЛПР, экспертами, техническим персоналом и техническими средствами.
Представление процесса принятия решений как логически упорядоченной совокупности неформальных и формальных процедур есть описание технологической схемы выполнения этого процесса. Такое описание позволяет структурно упорядочить процесс принятия решений и определить информационную модель процесса, на основе которой рационально организуется сбор, обработка и хранение необходимой информации.
В процессе принятия решений выделяют три этапа: постановка задачи, формирование решения и выбор решения. На этапе постановки задачи выполняются следующие процедуры:
выявление и описание проблемной ситуации;
определение времени, необходимого для принятия решения;
определение необходимых для принятия решения ресурсов.
Этап постановки задачи должен дать ответы на вопросы: какую проблему и в каких условиях нужно решать? когда нужно ее решать? какими силами и средствами будет решаться проблема?
На этапе формирования решений выполняются следующие процедуры:
· анализ проблемной ситуации;
· формирование ситуаций;
· формирование целей;
· определение ограничений;
· генерация решений;
· измерение предпочтений решений.
Основной целью второго этапа является формирование вариантов решений и оценка их предпочтений.
На этапе выбора решений выполняются следующие процедуры:
· определение допустимых (приемлемых) решений;
· формирование критериев выбора решения;
· определение эффективных (недоминируемых) решений;
· определение единственного решения.
Парадигма анализа решения
Простая парадигма анализа решения, которую мы рассмотрим, может быть сведена к процессу из пяти ступеней.
Предварительный анализ. Мы предполагаем, что лицо, принимающее решение, это какой-то один конкретный человек, который еще не решил, какой курс действий ему следует принять применительно к рассматриваемой конкретной проблеме. Сама проблема определена и известны возможные альтернативы действий.
Структурный анализ. Лицо, принимающее решение, проводит качественную структуризацию проблемы. Что он может выбрать уже сейчас? Выбор чего он может пока отложить? Каким образом он может построить свой выбор, основываясь на информации, получаемой в процессе анализа проблемы? Какие эксперименты он может провести? Какую информацию он может получить, предпринимая для этого специальные шаги, и что он может узнать в ходе нормального течения событий без специального вмешательства? Эти вопросы расположены по порядку на дереве решений (рис. 1.1).
Дерево решений имеет два типа вершин: вершины-решения (они обозначены квадратиками) и вершины-случаи (обозначаются кружками). В вершинах первого типа выбор полностью осуществляется лицом, принимающим решение. В вершинах же второго типа выбор не находится под полным контролем со стороны принимающего решение.
Анализ неопределенности. Лицо, принимающее решение, устанавливает определенные значения вероятности для тех ветвей, которые начинаются в вершинах-случаях. Установление значений этих вероятностей осуществляется с помощью совокупности совместно используемых методов и процедур, основывающихся на прошлых эмпирических данных, на допущениях и результатах различных стохастических, динамических моделей, на мнениях экспертов (после соответствующей калибровки, необходимой для того, чтобы учесть черты характера экспертов и смещения оценок, проистекающие из противоречивости позиций экспертов и их интересов), а также на субъективных суждениях лица, принимающего решение. Полученные значения вероятности следует проверить на наличие их внутренней согласованности.
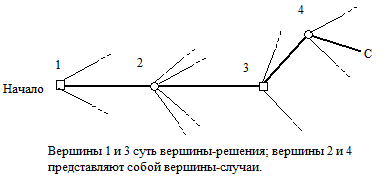 |
Рис. 1.1 Схематическое изображение дерева решений
Чтобы избежать недоразумений, связанных со специфическим видом дерева решений (см. рис. 1.1), мы сразу же укажем, что для некоторых вершин-случаев исходы могут представлять собой континуум в одно- или многомерном пространстве.
Анализ полезности или ценности. Следующим этапом является установление лицом, принимающим решение, численных значений полезности последствий, связанных с реализацией того или иного пути на дереве решений. На рис. 1.1 показан один возможный путь (от начала до точки С). Во всякой конкретной проблеме с каждым путем будут связаны различные экономические и психологические затраты и приобретения, которые существенны с точки зрения как лица, принимающего решение, так и других лиц, являющихся участниками решения проблемы. Всю совокупность подобных «затрат и приобретений», которые будут иметь место при реализации той или иной ветви, мы будем называть последствием, связанным с этой ветвью. Таким образом, каждая ветвь будет характеризоваться своим последствием. Затем предпочтительность этих последствий (со стороны лица, принимающего решение) должна быть представлена в виде чисел кардинальной полезности. Это представление не только отражает упорядочение (ранжирование) различных последствий с точки зрения предпочтений лица, принимающего решение (например, 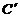 предпочитается С", которое, в свою очередь, предпочитается С"'), но и описывает его предпочтения относительно лотерей, построенных на этих последствиях. Допустим (рис. 1.2), что мы рассматриваем проблему выбора между действиями
предпочитается С", которое, в свою очередь, предпочитается С"'), но и описывает его предпочтения относительно лотерей, построенных на этих последствиях. Допустим (рис. 1.2), что мы рассматриваем проблему выбора между действиями 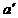 и
и 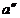 , т.е. фактически между лотереями
, т.е. фактически между лотереями 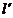 и
и 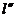 . Принимающий решение должен поставить в соответствие последствиям такие числа (
. Принимающий решение должен поставить в соответствие последствиям такие числа ( 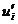 для
для 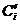 и
и 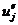 для
для 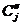 ), чтобы имело место соотношение
), чтобы имело место соотношение
( 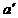 предпочтительнее
предпочтительнее 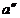 )
) 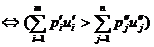 .
.
Другими словами, присваивание последствиям числовых значений полезности должно быть таким, чтобы для лица, принимающего решение, максимизация ожидаемой полезности соответствовала бы выбору им оптимального действия.
Процедуры оптимизации. После того как принимающий решение структуризирует свою проблему, установит соответствующие значения вероятности и полезности, оптимальная стратегия действий (оптимальная альтернатива) может быть найдена с помощью вычислений – оптимальной будет стратегия, которая максимизирует ожидаемую полезность. Этак стратегия указывает, что он должен делать в начале дерева решений и какой выбор должен произвести в каждому узле-решении, в котором он может оказаться на своем пути движения по дереву решений. Аналитик может применять различные методы для нахождения этой стратегии, но самыми простыми являются алгоритмы метода динамического программирования, и в частности алгоритм, основанный на «нахождении среднего и возвращения назад», с которым, как мы считаем, читатель уже знаком.

Рис. 1.2 Проблема выбора между двумя лотереями
Основные понятия
Функция принятия решений есть постоянно решаемая в процессе управления задача. Трактовка принятия решения как задачи позволяет более четко сформулировать ее содержание, определить технологию и методы ее решения.
Задача принятия решений направлена, на определение наилучшего (оптимального) способа действий для достижения поставленных целей. Под целью понимается идеальное представление желаемого состояния или результата деятельности. Если фактическое состояние не соответствует желаемому, то имеет место проблема. Выработка плана действий по устранению проблемы составляет сущность задачи принятия решений.
Проблемы могут возникать в следующих случаях:
· функционирование системы в данный момент не обеспечивает достижение поставленных целей;
· функционирование системы в будущем не обеспечит достижение поставленных целей;
· необходимо изменение целей деятельности.
Проблема всегда связана с определенными условиями, которые обобщенно называют ситуацией. Совокупность проблемы и ситуации образует проблемную ситуацию. Выявление и описание проблемной ситуации дает исходную информацию для постановки задачи принятия решений.
Субъектом всякого решения является лицо, принимающее решение (ЛПР). Понятие ЛПР является собирательным, Это может быть одно лицо — индивидуальное ЛПР или группа лиц, вырабатывающих коллективное решение,— групповое ЛПР. Для помощи ЛПР в сборе и анализе информации и формировании решений привлекаются эксперты — специалисты по решаемой проблеме. Понятие эксперта в теории принятия решений трактуется в широком смысле и включает сотрудников аппарата управления, подготавливающих решение, ученых и практиков специалистов.
Принятие решений происходит во времени, поэтому вводится понятие процесса принятия решений. Этот процесс состоит из последовательности этапов и процедур и направлен на устранение проблемной ситуации.
В процессе принятия решений формируются альтернативные (взаимоисключающие) варианты решений и оценивается их предпочтительность. Предпочтение — это интегральная оценка качества решений, основанная на объективном анализе (знании, опыте, проведении расчетов и экспериментов) и субъективном понимании ценности, эффективности решений.
Для осуществления выбора наилучшего решения индивидуальное ЛПР определяет критерий выбора. Групповые ЛПР производят выбор на основе принципа согласования.
Конечным результатом задачи принятия решений является решение, которое представляет собой предписание к действию. С содержательной точки зрения решением может быть способ действия, план работы, вариант проекта и т. п. Решение является одним из видов мыслительной деятельности и проявлением воли человека и имеет свои характерные признаки. К ним относятся:
· наличие выбора из множества возможных решений;
· выбор ориентирован на сознательное достижение целей;
· выбор основан на сформировавшейся установке к действию.
Первый признак определяет необходимость существования альтернативных решений. Если нет альтернатив, то нет выбора и, следовательно, нет и решения, поскольку отпадает необходимость в мыслительно-волевом акте. Важной особенностью решения является целенаправленность и сознательность выбора. Бесцельный выбор, импульсивное действие не рассматриваются как решение. Последний признак подчеркивает необходимость осуществления волевого акта при выборе решения. Решение должно приводить к действию, поэтому человек, принимающий решение, формирует его через борьбу мотивов и выработку установки — состояния готовности к действию.
Решение называется допустимым, если оно удовлетворяет ограничениям: ресурсным, правовым, морально-этическим. Решение называется оптимальным (наилучшим), если оно обеспечивает экстремум (максимум или минимум) критерия выбора при индивидуальном ЛПР или удовлетворяет принципу согласования при групповом ЛПР.
Обобщенной характеристикой решения является его эффективность. Эта характеристика включает эффект решения, определяющий степень достижения целей, отнесенный к затратам на их достижение. Решение тем эффективнее, чем больше степень достижения целей и меньше затраты на их реализацию.
Содержание задачи
В самой общей форме любая задача может быть представлена в виде «дано...», «требуется определить...». Руководствуясь этой формой, опишем содержание задачи принятия решений отдельно для индивидуального и группового ЛПР.
Для индивидуального ЛПР задача принятия решений записывается в виде
<So, T, Q|S, A, В, Y, f, К, Y*>, (1.3)
где слева от вертикальной черты расположены символы, описывающие известные, а справа неизвестные элементы задачи: So — проблемная ситуация; Т — время для принятия решения; Q — потребные для принятия решения ресурсы; S =(S1,..., Sn) — множество альтернативных ситуаций, доопределяющих проблемную ситуацию So; A=(A1, ..., Ak) —множество целей, преследуемых при принятии решения; В=(В1, ..., Bl)— множество ограничений;Y=(Y1,...,Ym) — множество альтернативных вариантов решения; f — функция предпочтения ЛПР; К— критерий выбора наилучшего решения; Y* — оптимальное решение.
В ряде случаев время и ресурсы на принятие решения могут быть неизвестны и подлежат определению самим ЛПР. Тогда необходимо располагать символы Т и Q в формуле (1.3) справа от вертикальной черты.
Рассмотрим более подробно элементы задачи принятия решений. Проблемная ситуация So описывается содержательно и, если это возможно, совокупностью количественных характеристик. Слово «ситуация» означает, что должны быть описаны условия, связанные с проблемой, причины ее возникновения и развития. Описание проблемной ситуации должно заканчиваться краткой содержательной формулировкой проблемы, которую необходимо решить.
В зависимости от характера задачи время на принятие решения Т может составлять секунды или часы, что характерно для оперативных задач, месяцы или годы — для долгосрочных задач. Располагаемое время существенно влияет на возможности получения полной и достоверной информации о проблемной ситуации и всестороннего обоснования последствий решений.
В качестве ресурсов Q для нахождения оптимального решения (но не его реализации) могут использоваться: знания и опыт ЛПР и экспертов, научно-технический потенциал исследовательских институтов, автоматизированные системы информационного обеспечения и управления и т. п.
В условиях неопределенности проблемная ситуация определена не полностью. Неопределенность может быть обусловлена различными факторами, например неизвестностью спроса на продукцию, неясностью в возможностях использования научно-технических достижений, климатическими факторами и другими причинами. В этих условиях для доопределения проблемной ситуации S0 необходимо сформулировать гипотетические ситуации (гипотезы, версии) Sj (j = 1, n), образующие конечное множество S =(S1, ..., Sn). Каждая ситуация Sj должна быть альтернативной всем остальным, т. е. все ситуации должны быть взаимоисключающими и, следовательно, независимыми. Совокупность ситуаций должна образовывать полную группу, т. е. охватывать все возможные ситуации, доопределяющие проблемную ситуацию S0. Каждая ситуация описывается содержательно с указанием набора количественных характеристик, среди которых важное значение имеет характеристика достоверности ситуации — вероятность ситуации рj. Для полной группы независимых ситуаций сумма вероятностей равна единице.
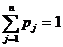
где n — количество ситуаций, составляющих полную группу.
Доопределение проблемной ситуации путем формирования полной группы альтернативных ситуаций уменьшает исходную неопределенность задачи, поскольку сформирован содержательный перечень возможных ситуаций и неопределенность описывается только вероятностями их свершения. В случаях когда неопределенность в проблемной ситуации отсутствует, отпадает необходимость формирования множества ситуаций (гипотез, версий). Случай полной определенности проблемной ситуации можно рассматривать как частный, вытекающий из случая неопределенности. Действительно, при полной определенности можно считать, что имеет место одна альтернативная ситуация с вероятностью единица, а другие ситуации имеют вероятности появления, равные нулю.
Для четкого определения желаемого состояния по устранению проблемной ситуации необходимо сформулировать множество целей A=(Ai, ..., Аk). Реальные задачи, как правило, многоцелевые и только в отдельных частных случаях может формулироваться единственная цель. Описание целей осуществляется содержательно и набором количественных характеристик. Наиболее важными характеристиками целей являются критерии достижения целей, показатели степени достижения целей и приоритеты —показатели важности целей.
Принятие решений всегда осуществляется в условиях различных ограничений: финансовых, материальных, правовых и т. п. Поэтому необходимо четко сформулировать множество ограничений В = (B1, ..., Вl), которые должны учитываться при принятии решения в конкретной проблемной ситуации.
Для достижения множества целей формируется множество альтернативных вариантов решений Y=(Y1, ..., Ym), из которых должно быть выбрано единственное оптимальное или приемлемое решение Y*. В множество возможных решений включается и решение о бездействии, при котором сохраняется проблемная ситуация. Решения описываются содержательно и формально — набором характеристик, в число которых обязательно включаются ресурсные характеристики, необходимые для реализации решений.
Функция предпочтения f(A, S, Y) используется для описания оценки решений по достижению целей в условиях возможных ситуаций. Функция предпочтения может описывать абсолютную или относительную оценку решений. Абсолютная оценка решений может быть произведена только в частных и весьма редких случаях. Поэтому в подавляющем числе реальных задач удается осуществить только сравнительную оценку решений. Эта оценка может носить качественный характер, тогда все альтернативные варианты решений упорядочиваются по предпочтению, или количественный характер, тогда можно сравнивать, на сколько или во сколько раз одно решение лучше другого.
Выбор наилучшего решения Y* производится по критерию выбора К, формулировку которого осуществляет ЛПР.
Суммируя изложенное, задачу принятия решения индивидуальным ЛПР можно кратко сформулировать следующим образом. В условиях проблемной ситуации S0, располагаемого времени Т и ресурсов Q необходимо доопределить ситуацию S0 множеством альтернативных ситуаций S, сформулировать множества целей А, ограничений В, альтернативных решений Y, произвести оценку предпочтений решений и найти оптимальное решение Y* из множества Y, руководствуясь сформулированным критерием выбора К.
Для группового ЛПР задача принятия решения записывается в виде
< S0, T, Q | S, A, B, Y, F(f), L, Y* > ,
где So, Т, Q, S, А, В, Y, Y* — те же самые символы, что и в задаче для индивидуального ЛПР; F(f) — функция группового предпочтения, зависящая от вектора индивидуальных предпочтений членов группы f=(f1, ..., fd), здесь d— количество членов в группе. Символ L в (1.4) означает принцип согласования индивидуальных предпочтений для формирования группового предпочтения. Выбор того или иного принципа определяет понятие наилучшего согласования. Широко известным принципом согласования индивидуальных предпочтений, образующим групповое предпочтение, является, например, принцип большинства голосов. Существуют и другие принципы согласования.
Таким образом, задача принятия решений групповым ЛПР формулируется следующим образом. В условиях проблемной ситуации So, располагаемого времени Т и ресурсов Q необходимо доопределить ситуацию. So множеством альтернативных ситуаций S сформулировать множество целей А, ограничений В, альтернативных вариантов решений Y, произвести индивидуальную оценку предпочтений решений, построить групповую функцию предпочтения F(f) на основе выбранного принципа согласования L и найти оптимальное решение Y*, удовлетворяющее групповому предпочтению.
Содержание задачи принятия решений позволяет сформулировать ряд утверждений, характеризующих особенности управленческих решений.
Во-первых, неизвестные элементы задачи: ситуации, цели, ограничения, решения, предпочтения — имеют прежде всего содержательный характер и только частично определяются количественными характеристиками. Количество неизвестных элементов задачи существенно больше, чем известных.
Во-вторых, определение неизвестных элементов задачи и в конечном итоге нахождение наилучшего решения не могут быть полностью формализованы, поскольку не существует методов и алгоритмов, позволяющих, например, сформулировать цели и варианты решения.
В-третьих, элементы задачи описываются характеристиками, часть из которых может быть измерена объективно, а для другой части возможно только субъективное измерение (например, приоритеты целей, предпочтения решений и т. п.).
В-четвертых, в ряде случаев приходится решать задачу принятия решений в условиях неопределенности, обусловленной неполным описанием проблемной ситуации и невозможность достаточно точной оценки ожидаемых последствий. В этих случаях на ряду с логическим мышлением важное значение имеет интуиция ЛПР.
В-пятых, принимаемые решения могут непосредственно затрагивать интересы ЛПР и экспертов. Поэтому мотивы их поведения влияют на выбор решения.
Перечисленные особенности подчеркивают отличие задачи управленческого решения от математической задачи нахождения оптимального решения, которая обычно формулируется как задача выбора наилучшего решения из множества заданных решений.
При изучении проблем построения целенаправленных систем всегда приходится учитывать цели, желания и нужды тех, кто управляет такими системами или сам подвергается их воздействию. Именно поэтому исследование полезности представляет собой основу теории и практики исследований операций.
В данной главе рассмотрены некоторые теоретические вопросы, относящиеся к структурам полезности, и заложены теоретические основы построения процедур для определения предпочтений в количественной форме.
Термин «полезность» имеет два разных значения. Первое (более важное) — это качественная, или сравнительная, оценка, характеризуемая такими утверждениями, как: «Я ценю это больше, чем то» или «Я предпочитаю х, а не у». Второе значение этого термина — количественная оценка, когда мы в виде числа выражаем наше предпочтение, пытаясь отразить его сравнительную природу. Вообще говоря, представление полезности в виде некоторого числа является удобным количественным •выражением исходного качественного отношения предпочтения. Учитывая такую двойственность, мы будем использовать термин «предпочтение» для отображения качественной характеристики объекта, а термин «полезность»— для количественного представления предпочтений.
Основы современной теории полезности были заложены в восемнадцатом столетии. Именно тогда несколько математиков, заинтересовавшись теорией вероятностей и ее применением к случайным играм и страхованию, выдвинули принцип (максиму), в соответствии с которым благоразумный человек, попав в критическую ситуацию, в которой возникла угроза его благосостоянию, должен вести себя так, чтобы максимизировать размер ожидаемого
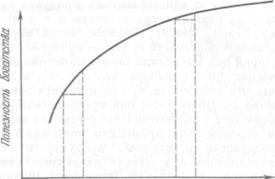
богатства или денежной прибыли. Вместо максимизации ожидаемой денежной прибыли, Крамер и Бернулли [1738] предложили максимизировать ожидаемую величину полезности. Чтобы можно было вычислить ожидаемую величину, они предположили, что для многих людей полезность богатства растет с убывающей скоростью по мере роста богатства. На рис. 1 хорошо проиллюстрирован этот так называемый закон убывающей предельной полезности: когда богатство возросло, то добавление еще одной единицы богатства приводит к меньшему возрастанию полезности, чем в начале роста благосостояния. Например, утверждалось, что некоторая персона, располагающая очень скромными средствами, может благоразумно предпочесть гарантированный подарок в девять тысяч дукатов обычной азартной игре в «орлянку», при которой выплачивается либо 20 тысяч дукатов, либо ничего.
х х+δ у у+δ
Величина богатства
Современная теория предпочтений исходит только из двух гипотез. Во-первых предполагается, что рассматриваемое множество вариантов решения, стратегий или способов решений не является пустым.
Во-вторых, предполагается бинарность предпочтений, что находит выражение во введении отношения предпочтение или безразличие на множестве альт ернатив.
2. Предпочтение и полезность
Основные положения
Под системой предпочтения ЛПР понимается совокупность его представлений о преимуществах и недостатках сравниваемых решений.
Решающее правило r (метод принятия решения) отражает информированность ЛПР о возможных исходах выбранных решений, а также предпочтительность тех или иных исходов. Решающее правило может быть заданно в виде аналитического выражения, алгоритма или словесной формулировки.
Фундаментальным понятием теории предпочтений является бинарное отношение, поэтому необходимо изложить некоторые положения теории бинарных отношений.
Бинарное отношения R на непустом множестве X есть подмножество множества всех упорядоченных пар элементов из X; множество всех упорядоченных пар задается прямым произведением 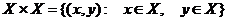 . Запись xRy (читается: x находится в отношении R к y) означает, что (x,y) принадлежит R; аналогично не xRy (записывается как
. Запись xRy (читается: x находится в отношении R к y) означает, что (x,y) принадлежит R; аналогично не xRy (записывается как 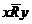 ) означает, что (x,y) не принадлежит R, или что x не находится в отношении R к y.
) означает, что (x,y) не принадлежит R, или что x не находится в отношении R к y.
Ниже указаны восемь возможных свойств бинарных отношений, разделенных на четыре группы. Во всех определениях предполагается, что х, у и z являются элементами множества X. Бинарное отношение R на множестве Х является:
1) рефлексивным, если xRx длякаждого 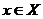 ; нерефлексивным, если
; нерефлексивным, если 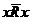 для каждого
для каждого 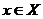 ;
;
2) симметричным, если из xRy следует yRx; асимметричным, если из xRy следует 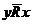 ;
;
3) транзитивным, если из xRy и yRz следует xRz; отрицательно транзитивным, если из 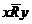 и
и 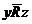 следует
следует 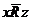 ;
;
4) связным, если xRy или yRx; слабосвязным, если из 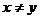 следует xRy или yRx.
следует xRy или yRx.
Пусть X — множество всех живых людей. Тогда отношение «выше, чем» является нерефлексивным, асимметричным, транзитивным и отрицательно транзитивным; отношение «ему (ей) столько же лет, как и» рефлексивно, транзитивно, отрицательно транзитивно и связно; отношение «является сестрой» (по крайней мере один из родителей общий) симметрично (но почему не транзитивно?); отношение «знаю имя», используемое при исследованиях пациентов с потерей памяти, не удовлетворяет ни одному из перечисленных свойств.
Предпочтение и безразличие
В теории предпочтений используются два основных бинарных отношения на множестве X. Во-первых, отношение нестрогого предпочтения >; запись х > у читается следующим образом: «х либо предпочтительнее, чем у, либо безразличен к у». Чаще пользуются формулировкой: «г/ не предпочтительнее, чем х». Во-вторых, применяется отношение предпочтения  ; запись х
; запись х  у читается так: «х предпочтительнее, чем у». Отношение нестрогого предпочтения чаще встречается в литературе, но в последнее время некоторые авторы стали пользоваться последним определением.
у читается так: «х предпочтительнее, чем у». Отношение нестрогого предпочтения чаще встречается в литературе, но в последнее время некоторые авторы стали пользоваться последним определением.
Когда в качестве основного бинарного отношения берется отношение нестрогого предпочтения (>;), то отношения предпочтения (  ) и безразличия (~) определяются через нестрогое предпочтение >~ следующим образом:
) и безразличия (~) определяются через нестрогое предпочтение >~ следующим образом:
х  у тогда и только тогда, когда х
у тогда и только тогда, когда х  ~ у, и неверно, что у
~ у, и неверно, что у  ~ х;
~ х;
х~ у тогда и только тогда, когда х  ~ у и у
~ у и у  ~ х. (1)
~ х. (1)
Если же в качестве основного бинарного отношения берется  , то отношение безразличия и отношение нестрогого предпочтения определяются на основе
, то отношение безразличия и отношение нестрогого предпочтения определяются на основе  как
как
х~ у тогда и только тогда, когда неверно х  у и неверно у
у и неверно у  х;
х;
х  ~ у тогда и только тогда, когда х
~ у тогда и только тогда, когда х  у или неверно х
у или неверно х  у
у
и неверно у  х.
х.
Транзитивность
Отношение предпочтения  на X транзитивно, если из того, что х предпочтительнее, чем у, а у предпочтительнее, чем z, следует, что х предпочтительнее, чем z. В целом это свойство кажется разумным, поэтому будем предполагать, что оно выполняется в большинстве дальнейших рассуждений. Транзитивность нарушается, если (х > у, у > z, х~ z) или (х
на X транзитивно, если из того, что х предпочтительнее, чем у, а у предпочтительнее, чем z, следует, что х предпочтительнее, чем z. В целом это свойство кажется разумным, поэтому будем предполагать, что оно выполняется в большинстве дальнейших рассуждений. Транзитивность нарушается, если (х > у, у > z, х~ z) или (х  у, у
у, у  z, z
z, z  х) для некоторых х, у и z из X.
х) для некоторых х, у и z из X.
Несмотря на очевидную разумность предположения о транзитивности предпочтений, имеется достаточно примеров и наблюдений, из которых видно, что здравомыслящие люди могут иметь нетранзитивные предпочтения в некоторых ситуациях (см. [10, 56, 59]). Альтернативы, используемые, чтобы проиллюстрировать этот факт, обычно включают несколько критериев или характерных признаков, как в следующем примере, когда молодому ученому предлагается выбрать место академической работы:
(а) х: ассистента в очень известном университете с окладом 15 тыс. долл.;
(б) у: доцента в университете штата N с окладом 18 тыс. долл.;
(с) z: профессора в малоизвестном колледже с окладом 21 тыс. долл.
Ученый предпочитает х больше, чем у, рассудив, что престиж известного университета стоит 3 тыс. долл.; исходя из аналогичных соображений, он предпочитает у больше, чем z, но, сравнивая х и z, он чувствует, что занимаемый пост и величина оклада перевешивают престижность, поэтому он предпочитает z по сравнению с х. В описанной ситуации его предпочтения образуют цикл х  y, y
y, y  z, z
z, z  х.
х.
Приведенный пример хорошо иллюстрирует проблему, возникающую в теории выбора, а именно то, что бинарное отношение не дает путеводной нити для выхода из цикла, не позволяет сделать выбор между х, у и z, когда каждая альтернатива менее предпочтительн
