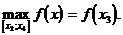Схема исследования функции на экстремум.

1. Найти О.О.Ф.

2. Найти в О.О.Ф.

3. Найти критические точки в О.О.Ф.:

4. а).в которых выполняется равенство ;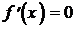

5. б) в которых не существует.

6. Изобразить на числовой оси О.О.Ф. и все ее критические точки.

7. Определить интервалы знакопостоянства производной в каждом из промежутков на которые критические точки разбивают О.О.Ф.

8. На основании достаточных условий экстремума сделать заключение о экстремуме функции в каждой из указанных в п.3 критических точках.

Пример 16. Исследовать на экстремум функцию .

Решение.

1). Функция определена при всех x ÎR.

2). .

3). Из уравнения находим х = -1; существует при всех х. Таким образом,
х = -1 – единственная критическая точка.

4). Точка х = -1 разбивает числовую ось на два промежутка (-¥; -1) и (-1; +¥).

5). Интервалы знакопостоянства производной :

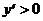на (-¥; -1), так как ;

на (-1; +¥), так как .

6). При переходе через точку х = -1 слева направо производная меняет знак с «+» на «-», значит х = -1 – точка максимума (х_тах = -1)

В точке х = -1 имеем y_max = y(x_max) = y(-1) = 8+2-1=9.

Ответ: х_тах = -1;

у_тах = 9.

Пример 17. Найти точки экстремума функции .

Решение. Производная этой функции определена во всех точках числовой оси и обращается в нуль в точке х = 3. В этой точке производная меняет знак с «+» на «-». Пользуясь признаком максимума, получаем, что точка х = 3 является точкой максимума.

Ответ:. х_тах = 3.

Пример 18. Найти экстремум функции .

Решение. О.О.Ф.: x Î R.

при х₁ = 2, х₂ = 3.

Ответ:

Пример 19. Исследовать на экстремум функцию .

Решение. О.О.Ф. найдем из решения системы:

.

Найдем производную:

.

в точке х =1. 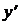не существует в точках х = 0 и х = 2.

Точки х = 0, х = 1, х = 2 не принадлежат О.О.Ф., следовательно, точек экстремума у этой функции нет.

Ответ: экстремум не существует.

Пример 20. Исследовать на экстремум функции

.

Решение. 1). О.О.Ф.: х ¹ 1.

2).

3). а) при х = 3 или при х = -1.

б) 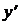не существует при х = 1, но эта точка не принадлежит О.О.Ф.

4). Отметим на координатной прямой критические точки х = -1, х = 3, х = 1.

5). Знаки производной отметим на полученных промежутках.

6). х = -1 – точка максимума, у_тах = -8

х = 3 – точка минимума, у_min = 0.

Ответ: x_max = -1, y_max =-8;

x_min = 3, y_min = 0.

Наибольшее и наименьшее значения непрерывной функции на отрезке.

Справочный материал.

1. Наибольшим (наименьшим) значением функции y=f(x) на промежутке X называется такое число M(m), что существует такая точка x₀, принадлежащая этому промежутку, что 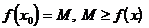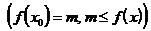для всех x из этого промежутка.

2. Наибольшее и наименьшее значения функции на промежутке X дифференцируемая функция f(x) может принимать либо на концах промежутка (если это числа), либо в критических точках, лежащих внутри промежутка.

3. На рис.1 функция y=f(x) достигает наибольшее значение на отрезке [a;b] в точке x=a и наименьшее значение в точке x=b:

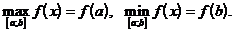
На интервале (a;b) в этом случае функция не достигает ни наименьшего ни наибольшего значений.

4. Если дифференцируемая функция f(x) на промежутке X имеет единственную точку экстремума и в этот экстремум – максимум (минимум), то в этой точке достигается наибольшее (наименьшее) значение функции.

5. На рис.1 функция y=f(x) на отрезке [x₁;x₃] в точке x=x₂ имеет единственный максимум:

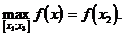
Функция y=f(x) на отрезке [x₂;x₄] в точке x=x₃ имеет единственный минимум: