Методы теории статистических решений.

В общем случае, сигналы в системе управления являются случайными величинами из-за помех различного рода. Поэтому необходимы методы анализа и выделения полезных сигналов из смеси сигналов и помех. Причём, с математической точки зрения такая смесь может быть как аддитивной, так и мультипликативной.

Введём следующие обозначения:

S_j — классы непересекающихся состояний или значений сигналов

y_i — наблюдаемые, измеряемые параметры сигналов (амплитуда, частота, фаза)

Тогда в соответствии с формулой Байеса получим:

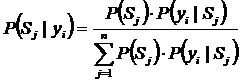
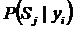— условная вероятность состояния S_j при условии наблюдения конкретных значений параметра y_i;

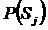— априорная вероятность состояния S_j;

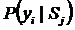— функция правдоподобия или условная вероятность (закон распределения) значений параметра y_i в состоянии S_j.

Обязательным условием реализации данной формулы являются знания (модельные или экспериментальные) функций правдоподобия.

Рассмотрим случай двух состояний (1 и 0) и одного параметра y. Рассмотрим отношения правдоподобия:

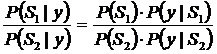
при условии 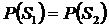получим:

P(S₁/y)/P(S₂/y) = P(y/S₁)/P(y/S₂)

Графическая интерпретация отношения правдоподобия.

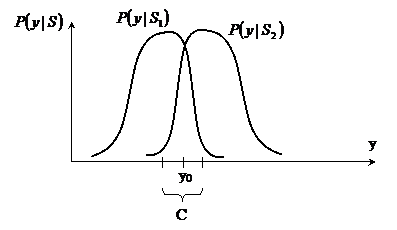
Выделим условно разделяющую поверхность (точку y₀). Данная точка подразумевает, что сигналы с параметрами y ≤ y₀ относятся к состоянию S₁, а y > y₀ к состоянию S₂. Очевидно, что такие статистические решения обладают ограниченной достоверностью (или соответствующими рисками).

Для математически строгого определения точки y₀ надо сформулировать соответствующие решающие правила:

а) правило максимального правдоподобия (вводит разделяющую точку y₀)

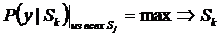
б) пороговое правило

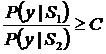
Особенностью пороговых правил является наличие области неопределенности, в пределах которой решение не может быть принято без дополнительной информации. При этом достоверность решений повышается, то есть понижаются риски ошибочных решений.

Рассмотрим правило максимального правдоподобия относительно разделяющей поверхности y₀. Введём весовые коэффициенты или стоимость ошибочных и правильных решений l_jk и будем учитывать априорные вероятности соответствующих состояний.

Формализуем эффективность или риски статистических решений относительно значения y₀ с соответствующими знаками (см. Рис.)

	правильное решение S1 → S1		ошибка S2 → S1

ошибка S1 → S2

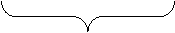
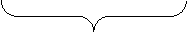
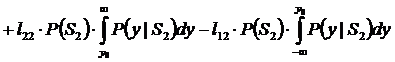
правильное решение S₂ → S₁

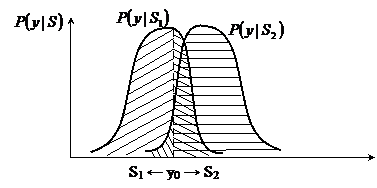
Для оптимизации значения y₀ выполним условие экстремума dR/dy =0 при (y=y₀). Тогда получим :

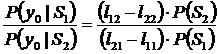
Пример:

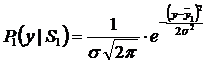
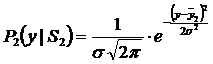
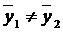- средние значения соответствующих функций правдоподобия;

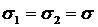- среднеквадратические отклонения функций правдоподобия.

Рассмотрим отношение правдоподобия и прологарифмируем его при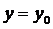

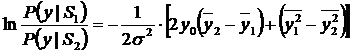
С другой стороны, из условия минимума функции R получим:

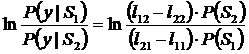при y=y₀

Приравнивая правые части данных выражений вычислим оптимальное значение величины y₀:

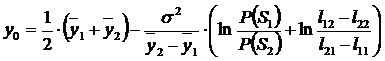
при условиях P(S₁) = P(S₂) и l_jk = l_kj получим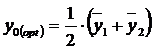

Последнее решение является очевидным (центр между средними значениями симметричных функций правдоподобия) и представляет вырожденный вариант, в котором не учитываются никакие дополнительные информационные факторы. В общем случае возможны следующие способы управления положением разделяющей точки y₀ и, соответственно, эффективностью или рисками статистических решений:

а) максимально возможное разнесение средних значений соответствующих функций правдоподобия при определённой дисперсии этих функций

б) сокращение дисперсий при неизменных средних значениях соответствующих функций правдоподобия

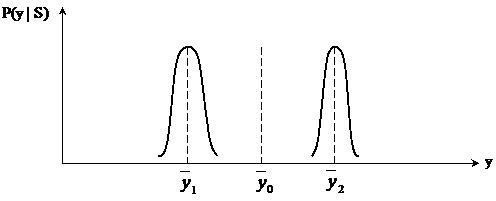
Данный вариант возможен при увеличении точности соответствующих измерительных приборов.

в) изменение положения y₀ за счёт учёта априорных вероятностей P(S_j)

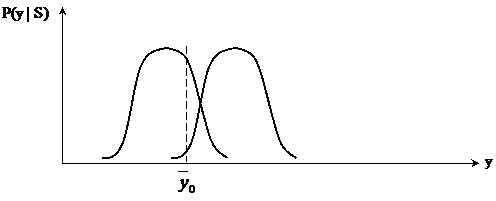
В ряде случаев данный способ используется в системах криптозащиты информации, основанной на соответствующем кодировании алфавита.

г) изменение положения точки y₀ за счёт влияния коэффициентов l_jk:

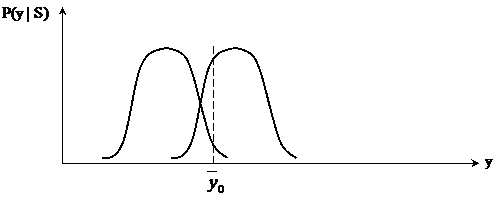
При этом изменяются вероятности соответствующих ошибок первого и второго рода. Данный способ применяется при несимметричной стоимости ошибок 1 и 2 рода, в частности в системах ПВО.

Общим способом повышения эффективности решающих правил (обнаружение полезных сигналов на фоне помех) является способ увеличения информативности параметров y за счёт комплексирования множества таких параметров.

Следует отметить, что в данном конспекте рассмотрен частный вариант применения статистических методов в теории управления. Вообще область применения теории случайных процессов в САУ значительно шире – см. рекомендованную литературу.