Тема: Методика изучения элементов геометрии в начальном курсе математики

План:

1. Задачи изучения геометрического материала.

2. Общие вопросы методики работы над геометрическим материалом.

3. Задачи геометрического содержания.

4. Формирование представлений и понятий о геометрических фигурах:

- существенные и несущественные признаки;

- содержание и объем понятия;

- классификация понятий.

5. Последовательность работы по подготовке и изучению периметра прямоугольника (квадрата):

- выяснение общих представлений младших школьников о прямоугольнике;

- знакомство с понятием «прямоугольник» на основе суждения понятия «многоугольник»;

- прямые и непрямые углы;

- изучение свойств прямоугольника, практическое их обоснование.

6. Возможные ошибки в рассуждениях учащихся при изучении геометрического материала.

Рекомендательная литература

1. Абдуллаева К. Пути устранения некоторых геометрических ошибок учащихся // Начальная школа. – 1978. - №2. – С. 14-17.

2. Коган Т.Л. Формирование геометрических понятий // Начальная школа. – 1981. - №2. – С. 26-28.

3. Крайнюк В.М. Практическая направленность в изучении геометрического материала // Начальная школа. – 1980. - №1. – С. 4-36.

4. Колягин Ю.М., Тарасова О.В. Наглядная геометрия в начальных классах // Начальная школа. – 1996. - №9. – С. 70-74.

5. Левенберг Л.Ш. Практическая направленность в изучении геометрического материала // Начальная школа. – 1982. - №10. – С. 47-50.

6. Пазушко Ж.И. Развивающая геометрия в начальной школе // Начальная школа. – 1999. - №1. – С. 93-95.

7. Савенков А.И. Задачи для развития объемно-пространственного мышления школьников // Начальная школа. – 1998. - №7. – С. 59-63.

8. Шмырева Г.Г. Практические работы при ознакомлении с геометрическими фигурами в 1-м классе // Начальная школа. – 1982. - №10. – С. 54-57.

Основное содержание геометрического материала, включенного в программу и реализованного в системе тщательно отобранных задач, направлено на формирование достаточно полной системы геометрических представлений (включающей образы геометрических фигур, их элементов, отношений между фигурами, их элементами).

На этой основе формируются пространственные представления и воображение, развивается речь и мышление учащихся, организуется целенаправленная работа по формированию важных практических навыков. Важнейшей задачей учителя является определение методики, раскрывающей содержание геометрического материалана том уровне, который должен быть достигнут учащимися к моменту их перехода в IV класс, а также ведущих направлений изучения этого материала.

Для формирования геометрических представлений работа должна проводиться следующим образом: свойства фигур учащиеся выявляют экспериментально, одновременно усваивают необходимую терминологию и навыки; основное место в обучении должны занимать практические работы учеников, наблюдения и работы с геометрическими объектами.

Оперируя разнообразными предметами, моделями геометрических фигур, выполняя большое число наблюдений и опытов, учащиеся подмечают наиболее общие их признаки (не зависящие от материала, цвета, положения, массы и т. п.).

В методике формирования геометрических представлений важно идти от «вещи» к фигуре (к ее образу), а также наоборот - от образа фигуры к реальной вещи.

Это достигается систематическим использованием приема материализации геометрических образов. Например, прямая линия не только вычерчивается с помощью линейки, представление о ней дает и край - ребро линейки, натянутая нить, линия сгиба листа бумаги, линия пересечения двух плоскостей (например, плоскости стены и плоскости потолка). Отвлекаясь от конкретных свойств материальных вещей, учащиеся овладевают геометрическими представлениями. Так, например, можно видоизменять способ деления многоугольника отрезком на части. Вначале это может быть перегибание бумажного многоугольника (рис.). В этом случае отрезок (линия сгиба) реально делит многоугольник на 2 части. Этот опыт полезно продолжить, разрезав многоугольник по линии сгиба на 2 многоугольника. Несколько позже эту же задачу полезно решить на чертеже, вначале путем непосредственного проведения (вычерчивания) отрезка (рис.), затем прикладыванием указки (рис.).

В I классе в основном завершается первоначальное ознакомление с фигурами и их названиями. Это делается на основе рассмотрения окружающих вещей, готовых моделей и изображений фигур. У детей постепенно вырабатывается схема изучения фигур, схема их анализа и синтеза, облегчающая усвоение свойств каждой фигуры.

Значительное место в методике должно отводиться применению приема сопоставления и противопоставления геометрических фигур. В I классе это позволит из множества фигур наглядно (без помощи определений) выделять множество кругов, множество многоугольников, множество линий и т. д.; во II и III классах - уточнять свойства фигур, классифицировать их. Больше внимания следует уделять противопоставлению и сопоставлению плоских фигур (круг - многоугольник, окружность - круг и т. д.); плоских и пространственных фигур (квадрат - куб, круг -шар и пр.).

Причем эта работа должна проходить не только на уроках математики, но и на уроках труда и особенно на уроках рисования, когда воспроизведение формы предмета зависит от качества и глубины анализа его геометрической формы. Например, при наблюдении куба (или предмета, имеющего форму куба) следует найти в нем характерные точки, отрезки, многоугольники; при наблюдении шара можно обратить внимание на его круглые сечения.

Уже при первоначальном ознакомлении детей с геометрическими фигурами в I классе дети выполняют умственные операции анализа и синтеза. Важной задачей учителя, определяющей методику обучения в этот момент, является анализ фигуры, на основе которого выделяются ее существенные свойства (признаки) и несущественные. Так, например, существенным для треугольника будет не его положение на плоскости (листе бумаги), не относительные размеры сторон, а наличие трех сторон (углов, вершин); для прямоугольника существенно то, что он четырехугольник (четыре угла) и все его углы прямые. Все остальное не существенно.

В процессе обучения возникает потребность применения геометрической и логической терминологии, символики, чертежей. Так, уже во II классе введение буквенной символики помогает не только различать фигуры и их элементы, но и является одним из средств формирования обобщений. Например, запись ОК < 5 см говорит учащимся о том, что отрезок ОК любой отрезок, имеющий длину меньшую, чем 5 см.

Как показывает опыт обучения математике в I-IV классах, под влиянием той легкости и интереса, с которыми учащиеся I-IV классов воспринимают не только очевидные простые, но иногда трудные геометрические факты, учитель начинает недооценивать наглядный и практический подход к изучению геометрического материала, не выполняет минимума упражнений, помещенных в учебнике, обращает мало внимания на формирование практических навыков. Такой учитель встает на неверный и опасный путь формального ознакомления младших школьников с геометрическими фигурами. Он начинает знакомить детей с фигурами не путем их наблюдения, изготовления из бумаги и вычерчивания, а сообщая формальное определение, только словесным способом.

В процессе определения понятия каждый раз одно понятие (например, «квадрат») определяется через другое, более широкое («прямоугольник»), которое в свою очередь также может быть определено через еще более широкое понятие («параллелограмм», «четырехугольник», «многоугольник»). Такую цепь определений нельзя продолжать бесконечно. В конце концов мы приходим к понятиям, наиболее широким и общим, для которых невозможно указать ближайший род. Такие понятия называют основными (первичными или неопределяемыми).

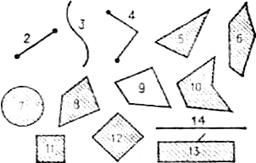
Рис.

Высокого уровня усвоения достигается при осуществлении связи изучения геометрического материала с другим материалом начального курса математики. В основе этой связи лежит возможность установления отношений между числом и фигурой, свойствами чисел и свойствами фигур. Это позволяет использовать фигуры при формировании понятия числа, свойств чисел, операций над ними и, наоборот, использовать числа для изучения свойств геометрических образов и их отношений.

1.В 1 классе фигуры следует применять наряду с другими материальными вещами как объекты для пересчитывания. Несколько позже такими объектами должны стать элементы фигур, например вершины, стороны, углы многоугольников. Учащиеся постепенно знакомятся с измерением отрезков.

2.Это позволяет устанавливать связь между отрезками и числами. Во II классе устанавливается прямая связь между отрезками (точками) и числами.

3.Геометрические фигуры используются при ознакомлении учащихся с долями. В указанных выше случаях открывается, больше возможностей органически связать изучение геометрических объектов с арифметическим материалом, включенным в курс математики I-IV классов.

Уже в I-IV классах выполняются простейшие классификации углов (прямые и непрямые), многоугольников (по числу углов) и т. д. Изучение родовых и видовых понятий готовит детей к пониманию определений, построенных на указании рода и видовых отличий.

Это дает, например, возможность построить методику ознакомления с прямоугольниками таким образом, что в дальнейшем ученики усваивают, что любой квадрат есть прямоугольник.

4.Использование упражнений, в которых дети отмечают (выделяют) точки, принадлежащие или не принадлежащие фигуре или нескольким фигурам, помогает в дальнейшем трактовать геометрическую фигуру как множество точек.

5.Это позволяет более осознанно выполнять операции деления фигуры на части или получения фигуры из других (складывание), т.е. выполнять по существу операции объединения, пересечения, дополнения над точечными множествами.

Важной общей методической линией осуществления связи в изучении геометрического материала с остальными вопросами курса начальной математики является, таким образом неявная опора на теоретико-множественные и простейшие логико-математические представления в изучении фигур, их отношений, свойств.

6.Общим методическим приемом, обеспечивающим прочные геометрические знания, является формирование пространственных представлений через непосредственное восприятие учащимися конкретных реальных вещей, материальных моделей геометрических образов. В I классе пространственные представления вырабатываются в процессе приобретения детьми практического опыта при изучении отношений взаимного положения предметов, выражаемых словами «выше», «ниже», «справа», «в середине», «слева», «между», «внутри», «вне», «над», «под», «снизу», «сверху», «спереди», «сзади» и т. д. Во II-III классах характер работы по формированию пространственных представлений усложняется. Например, представления об одной фигуре формируется с опорой на другую. Так, опираясь на представления о треугольнике вообще, можно получить представления о прямоугольном треугольнике.

7.Учитель должен систематически проводить работу по формированию умений и навыков применения чертежных и измерительных инструментов, построению изображений геометрических фигур, умений описывать словесно процесс работы, выполняемой учеником, и ее результат, умений применять усвоенную символику и терминологию. Важным методическим условием реализаций этой системы является сначала осознанное выполнение действий и лишь затем автоматизация этих действий.

Результатом обучения в I-IV классах должно быть формирование первоначальных представлений о точности построений и измерений.

В I классе учащиеся овладевают навыками измерения и построения отрезков с помощью линейки (с точностью до 1 см). При этом детям предъявляются не меньшие требования, чем это обычно делается, например, в отношении навыков письма. Во II- IV классах в практику измерений и построений постепенно вводятся новые инструменты: циркуль, циркуль-измеритель, чертежный треугольник, рулетка. Повышаются требования к точности построений и измерений, к качеству чертежей и моделей, выполняемых детьми, к описанию хода и результатов проделанной работы.

Работа по формированию навыков должна проводиться распределение и постепенно почти на каждом уроке (и не только на уроках математики). Это создает условия для более частого применения этих навыков в учебной и практической деятельности, обеспечивает необходимую их прочность.

Для правильного выбора методики обучения младших школьников учитель должен иметь общие представления о системе задач, представленных в учебниках. Эта система включает в каждом классе задачи:

а) в которых геометрические фигуры используются как объекты для пересчитывания (круги, многоугольники, элементы многоугольников). При решении таких задач в основном усваивается необходимая терминология и образуются умения узнавать и различать фигуры;

б) связанные с формированием представлений о геометрических величинах (длине, площади) и навыков измерения отрезков, площадей фигур;

в) вычислительные, связанные с нахождением периметра многоугольников, площади прямоугольника;

г) на элементарные построения геометрических фигур на клетчатой бумаге, на гладкой нелинованной бумаге с помощью линейки, угольника, циркуля (без учета размеров);

д) на элементарные построения фигур с заданными параметрами (треугольник с прямым углом, прямоугольник с заданными сторонами и т. д.);

е) на классификацию фигур;

ж) на деление фигур на части (в том числе на равные части) и на составление фигур из других;

з) связанные с формированием основных навыков чтения геометрических чертежей, использованием буквенных обозначений (формированием «геометрической зоркости»);

Последние изменения программы по математике в начальной школе характеризуются тенденцией усиления внимания к изучению геометрического материала. Так, уже в 1 классе дети знакомятся с такими геометрическими фигурами как точка, линия (прямая, кривая), отрезок, ломаная, многоугольник и его элементы (углы, вершины, стороны), изучение перечисленного геометрического материала не вызывает, как правило, каких либо затруднений у детей.

Начальный период адаптации – примерно один месяц – совпадает с проведением подготовительной работы к восприятию понятий числа, отношения, величины и др.

В начальном курсе математики его называют дочисловым периодом. Дети в этот период учатся целенаправленно проводить наблюдения над предметами и группами предметов, расположением их в пространстве, сравнение по одному или нескольким признакам. Одновременно с обобщением их жизненного опыта, расширением математического кругозора, обучение их организованности, самостоятельности. Большое внимание на этом этапе уделяется развитию математической речи детей, что способствует развитию у них логических умений.

Младший школьник начинает входить в учебную деятельность. На этом этапе следует уделять большое внимание развитию пространственных представлений у первоклассников, в содержание которого входит геометрический материал. Учителя недооценивая его знания уделяют недостаточно времени изучению геометрических фигур. В результате к концу обучения у ребенка слабо сформированы чертежные навыки, умение выделять и обосновывать свойства геометрических фигур, решать простейшие задачи на построение.

Поэтому в работе с первоклассниками изучение первых геометрических понятий можно включить в этот период. Изучение их может проходить не только на уроках в классе, но и на уроках – играх с использованием самого разного дидактического материала, на уроках – экскурсиях (в парках, на улицах города, на пришкольном участке, при проведении подвижных игр с различными заданиями). На геометрическом материале могут быть рассмотрены следующие вопросы программы:

1. Признаки предметов, сравнение предметов по цвету, размеру, форме;

2. Пространственные представления, взаимное расположение предметов;

3. Счет предметов.

Тем самым обеспечивается накопление обобщения жизненного опыта ребенка, реальных ярких впечатлений, которые очень важны для познания детьми окружающего.

Проведенные занятия, наблюдения необходимо осмыслить первоклассникам вместе с учителем, обобщены, включены в формирующуюся систему представлений ребенка о мире. Оптимальные условия для всего перечисленного создают уроки изучения геометрического материала.

Первые дни ребенка в школе не проходят гладко, без стрессов. Задача учителя на этом этапе работы сделать его менее болезненным для психики первоклассника. Одним из способов в этом видится в использовании его резервных возможностей, его жизненного опыта: желание ребенка быть самостоятельным, организованным, умение играть с ровесниками, проявление инициативы.

Уроки математики в период адаптации ребенка к обучению представляют ему наилучшую возможность. Здесь можно на основе выше перечисленных свойств личности ребенка, обобщении, уточнении его представлений о данном понятии познакомить с новыми. С этой целью проанализируем урок математики, проведенный по теме «Прямая. Кривая. Отрезок.»

Прямая. Кривая. Отрезок.

Цель урока:

1. На основе обобщения жизненного опыта ребенка сформировать представления о геометрических фигурах (точка, прямая, кривая, отрезок).

2. Развивать у первоклассников мыслительные операции (сравнение, умение обобщать, находить закономерность),

3. Связать полученные знания с окружающими предметами.

Оборудование: магнитная доска с набором цветных магнитов – «точек», линейка, шнур, ленты разного цвета, ножницы, у каждого ребенка на столе – цветные полоски из бумаги.

Ход урока

Актуализация знаний.

1. Устно. Я называю число, а тот, кого спрошу, с него продолжает счет:

5 (6, 7, 8, 9, 10)

3 (4, 5, 6, 7, …)

А теперь в обратном порядке:

7 (6, 5, 4, 3, 2, 1)

4 (3, 2, 1)

9 (8, 7, 6, 5, 4, 3, 2, 1)

- Как удобно считать – в прямом или обратном порядке? (в прямом)

- Почему? ( мы так привыкли)

- С какого числа мы начинаем счет? (с числа 1)

- Возьмите в руки полоски бумаги, образуйте с их помощью цифру 1 и покажите. (Дети берут по 2, 3 палочки, показывают).

- Если не догадываются, я их прошу:

- А сможете показать цифру 1, используя только одну палочку? (Да, надо ее согнуть).

- Какая сначала была полоска? (ровная, прямая)

- А какая стала? (кривая)

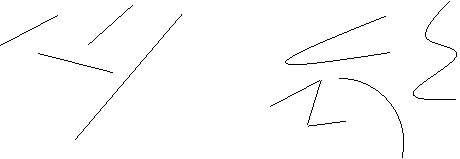II Объяснение нового. 1. На доске с двух сторон начерчены прямые и непрямые линии:

- Что начерчено на доске? (разные линии)

- А почему – в разных местах? Чем они отличаются? (прямые и кривые).

- Кто сможет показать, как я чертила кривые линии? Начертите рядом еще кривые линии. (Дети выходят и мелом чертят их).

- А как начертить прямые? (Дети пытаются начертить без линейки – не получается. Постепенно приходят к выводу – нужна линейка).

- Кто ответит - при помощи чего вычерчивают прямые и кривые линии? (прямые - при помощи линейки, а кривые – без нее как угодно).

- Итак, какие линии мы чертили? (прямые и кривые).

1. Учитель вызывает к доске двух учеников и дает им в руки – концы шнура (или ленты).

- Встаньте так, чтобы у вас получилась прямая линия. (Дети, держат шнур за концы и отходят друг от друга так, чтобы шнур был натянут).

- А теперь что нужно сделать, чтобы линия получилась кривая? (Нужно приблизиться, шагнуть друг к другу).

- Еще раз образуйте прямую линию. (Дети отходят так, чтобы шнур натянулся).

2. Учитель берет в руки ножницы, подходит к детям, которые держат шнур, отрезает его с двух сторон и к месту среза приставляет магнит красного цвета:

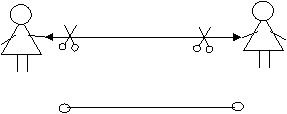Двое детей, стоящие у доски, держат в руках отрезанный шнур и магнит.

- Что я сделала со шнуром? (Отрезали)

- Была прямая линия. Как ее теперь можно назвать. (Если дети сами не догадываются можно объяснить, что в математике эту фигуру называют отрезок).

3. На магнитной доске учитель крепит два магнита и через них перевешивает нитку.

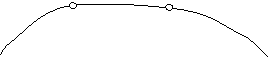- При помощи двух магнитов и шнура какую фигуру я смогу изобразить? (отрезок).

- Чтобы начертить на доске кривую – что нам потребуется в помощь? (мел).

- Что еще нужно, чтобы начертить прямую? (мел, линейка)

- А как мне начертить прямую? Это часть прямой или кривой линии? (часть прямой).

- Что еще мы делали с прямой линией, когда из нее образовывали отрезок? (мы ее отрезали и на место показывали магнитом).

- Как это сделать на доске? Что поставим вместо магнита? (Точки).

- Сколько точек нужно поставить, чтобы провести один отрезок? (Одна, две).

Дети по очереди выходят к доске и пробуют начертить отрезок, постепенно приходят к выводу, что нужно две точки, чтобы через них провести один отрезок.

- У себя в тетради поставьте одну точку и через нее проведите отрезки. Сколько их получилось? (У детей получается разное количество лучей, прямых).

- А теперь - ниже поставьте две точки и проведите через них отрезки. Сколько их получилось? (Одна).

III Итог урока. У вас на столе полоски бумаги. Покажите самую длинную из них. (Дети поднимают ее, показывают учителю).

- Какая это линия – прямая или кривая? (прямая).

- Как из нее получить кривую? (Согнуть).

- На концах полоски красным карандашом поставьте точки. Какая фигура получилась? (отрезок).

- Итак, какие новые фигуры мы сегодня узнали? (прямая, кривая, отрезок).

Во 2 классе дети знакомятся с такими геометрическими фигурами, как угол, прямоугольник, квадрат и их свойствами. Опишем методику изучения этих фигур более подробно.

Прямой угол

Понятие прямого угла носит не столько самостоятельную, сколько вспомогательную роль – подготовить детей к введению понятий прямоугольника и квадрата. По традиционной программе в начальной школе дети знакомятся с двумя видами углов: прямые и непрямые. В большинстве авторских программ (Н.Б. Истоминой, И.И. Аргинская, Л.Г. Петерсон и др.) кроме прямых особо выделяются острые и тупые углы:

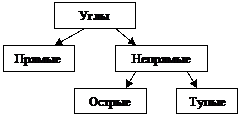
С углом, как составной частью многоугольника, дети знакомятся еще с 1 класса. Основная задача на данном этапе – сформировать представление о прямом угле. Это можно сделать следующим образом. Предложите ребенку взять несколько листов бумаги и каждый из них дважды сложить пополам («уголком»). Сравнивая после этого полученные углы между собой путем их наложения друг на друга, приходим к выводу, что все они равны, независимо от того, в каком направлении мы перегибали листы. Полученный угол называется прямым.

Сформировав представление о прямом угле, необходимо научить ребенка находить прямые углы как в окружающей обстановке (углы стола, окна, стены и т.д.), так и в составе геометрических фигур (различного вида многоугольников). В случае затруднения визуального определения («на глаз»), в качестве эталона используется прямой угол стандартного прямоугольного треугольника. После того, как данное умение сформировано, можно переходить к знакомству с прямоугольником.

Прямоугольник

Для знакомства с прямоугольником предварительно заготовьте 8-9 четырехугольников, вырезав их из цветной бумаги так, чтобы среди них было 3-4 прямоугольника с разным соответствием сторон.

Предложите ребенку с помощью эталона определить, сколько в каждом четырехугольнике прямых углов, и полученное число записать на каждой фигуре. Попросите показать четырехугольники, у которых только один прямой угол, два прямых угла, совсем нет прямых углов. Есть ли четырехугольники, у которых все углы прямые? Отложите их в сторону. Четырехугольники, у которых все углы прямые, называются прямоугольниками.

Таким образом, у понятия «прямоугольник» два существенных признака: 1) это должен быть четырехугольник; 2) у него все углы должны быть прямыми. Если хотя бы один из этих признаков не выполняется, то данная фигура не является прямоугольником.

Знакомство с квадратом осуществляется так же, как и с прямоугольником. заготовьте заранее 7-8 прямоугольников, среди которых 2-3 квадрата. Предложите ребенку самому определить, какие из предложенных фигур чем-то отличаются от остальных. Если это задание вызовет затруднение, попросите сравнить длины сторон каждого прямоугольника. Тем самым из всего класса прямоугольников будут выделены те, у которых все стороны равны. Такие прямоугольники называются квадратами.

Таким образом, у понятия «квадрат» два существенных признака: 1) это прямоугольник; 2) у него все стороны равны.

Замечание. Сложность в соотнесении понятий «прямоугольник» и «квадрат» состоит в том, что квадрат является частным случаем прямоугольника. По этой причине дети не видят в квадрате прямоугольник. В этом можно убедиться на простом примере. Предложите ребенку посчитать, сколько прямоугольников следующей фигуре:

Некоторые дети видят в ней 2 прямоугольника, другие – три (кроме двух маленьких, еще – самый большой), третьи – обнаруживают, что два маленьких вместе тоже составляют прямоугольник. Однако не все дети видят прямоугольник в расположенном слева квадрате. Попытка взрослого обратить на это внимание нередко вызывает возражение со стороны ребенка, убежденного в том, что это не прямоугольник, а квадрат. Логические аргументы тоже не всегда помогают. Приведем типичный диалог.

- Давай рассуждать так, - предлагает взрослый. – Что такое прямоугольник?

- Это четырехугольник, у которого все углы прямые, - заученно отвечает ребенок.

- Эта фигура четырехугольник? – спрашивает взрослый, показывая на квадрат.

- Да, - соглашается тот, еще не понимая, к чему клонит взрослый.

- У него все углы прямые?

- Все, - внимательно осмотрев рисунок, подтверждает ребенок.

- Значит это прямоугольник? – задает последний вопрос взрослый, уверенный в том, что сила логики наконец-то восторжествует.

- Нет, это квадрат, - с безмятежной внутренней уверенностью отвечает тот.

Этот феномен свидетельствует о том, что многие дети данного возраста в своих суждениях опираются не на логические законы, а на внешнее восприятие, которое для них выступает более убедительным аргументом.